Turunan
| Kalkulus |
|---|

Dalam matematika, turunan atau derivatif dari sebuah fungsi adalah cara mengukur sensitivitas perubahan nilai fungsi terhadap perubahan pada nilai variabelnya. Sebagai contoh, turunan dari posisi sebuah benda bergerak terhadap waktu mengukur kecepatan benda bergerak ketika waktu berjalan. Turunan adalah alat penting dalam kalkulus.
Turunan sebuah fungsi satu variabel di suatu titik, jika itu ada, adalah kemiringan dari garis singgung dari grafik fungsi di titik tersebut. Garis singgung adalah hampiran (aproksimasi) linear terbaik dari fungsi di sekitar titik tersebut. Konsep turunan dapat diperumum untuk fungsi multivariabel. Dalam perumuman ini, turunan dianggap sebagai transformasi linear, dengan translasi yang sesuai, menghasilkan hampiran linear dari grafik fungsi multivariabel tersebut. Matriks Jacobi adalah matriks yang merepresentasikan transformasi linear terhadap suatu basis yang ditentukan. Matriks ini dapat ditentukan dengan turunan parsial dari variabel-variabel independen. Pada fungsi multivariabel bernilai real, matriks Jacobi tereduksi menjadi vektor gradien.
Proses menemukan turunan disebut diferensiasi. Kebalikan proses ini disebut dengan antiturunan. Teorema fundamental kalkulus menyatakan hubungan diferensiasi dengan integrasi. Turunan dan integral adalah dua operasi dasar dalam kalkulus satu-variabel.
Konsep turunan fungsi yang universal banyak digunakan dalam berbagai cabang matematika maupun bidang ilmu yang lain. Dalam bidang ekonomi, turunan digunakan untuk menghitung biaya marginal, total penerimaan, dan biaya produksi. Bidang biologi menggunakan turunan untuk menghitung laju pertumbuhan mikroorganisme, dalam bidang fisika untuk menghitung kepadatan kawat, dalam bidang kimia untuk menghitung laju pemisahan, dalam bidang geografi untuk menghitung laju pertumbuhan penduduk, dan masih banyak lagi.
Pendahuluan[sunting | sunting sumber]
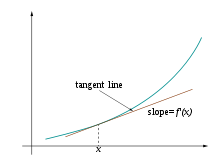
Secara informal, turunan dari sebuah fungsi y = f(x) dengan variabel x adalah ukuran dari rasio perubahan nilai y terhadap perubahan nilai variabel x. Jika x dan y adalah bilangan real, dan jika grafik fungsi f diplot terhadap x, besar turunan dari fungsi ini pada sembarang titik menandakan kemiringan dari grafik fungsi pada titik tersebut.

Kasus sederhana dari fungsi f(x) adalah fungsi linear yang memiliki persamaan y = f(x) = mx + b, dengan bilangan real m dan b. Kemiringan dari fungsi ini, m, dinyatakan dengan
dengan simbol Δ (Delta) adalah singkatan untuk "perubahan nilai", dan simbol dan masing-masing menyatakan besar perubahan yang terjadi. Sebagai contoh,
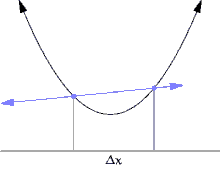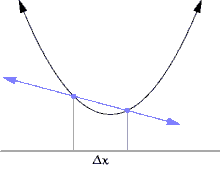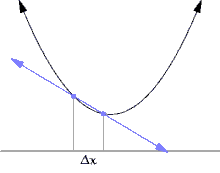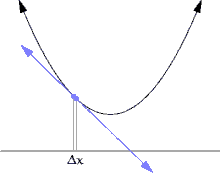
Jika fungsi f tidak linear (maksudnya grafik fungsi bukan berupa garis lurus), maka perubahan nilai y dibagi dengan perubahan nilai x dapat berubah-ubah tergantung nilai perubahan nilai x yang dipilih. Turunan adalah metode untuk menentukan nilai unik dari perbandingan perubahan nilai tersebut, yang tidak tergantung besar perubahan melainkan titik x yang dipilih. Metode menentukan turunan dapat diilustrasikan lewat Gambar 1 sampai Gambar 3, yang menggambarkan nilai limit dari perbandingan Δy / Δx dengan besar Δx menuju 0.
Asal-usul definisi[sunting | sunting sumber]
Salah satu cara umum untuk menyatakan cara diferensiasi yang intuitif ke dalam definisi yang matematis adalah dengan mendefinisikan turunan sebagai limit dari perbandingan dua bilangan real.[1] Pendekatan ini dapat dijabarkan sebagai berikut.
Misalkan f adalah fungsi bernilai real yang terdefinisi pada suatu lingkungan buka dari suatu bilangan real a. Dalam geometri, garis singgung dari grafik fungsi f di a adalah suatu garis unik yang melalui titik (a, f(a)) dan tidak memotong fungsi f di sekitar titik (a, f(a)). Turunan dari y terhadap x di a secara geometris adalah besar kemiringan dari garis singgung grafik f di (a, f(a)). Besar kemiringan garis singgung akan sangat mirip dengan besar kemiringan garis yang melalui titik (a, f(a)) dan sebuah titik lain di grafik yang dekat dengannya, sebagai contoh (a + h, f(a + h)). Garis yang didefinisikan ini disebut dengan garis sekan. Nilai h yang dekat dengan nol akan memberikan hampiran (dugaan, aproksimasi) yang baik mengenai besar kemiringan garis singgung; dan secara umum, nilai (mutlak) h yang semakin kecil akan memberikan hampiran yang lebih baik. Besar kemiringan m dari garis sekan adalah perbedaan nilai y antara dua titik tersebut, dibagi dengan perbedaan nilai x pada dua titik yang sama, dengan kata lain
Jika nilai limit ada, f dikatakan terdiferensialkan di a. Notasi adalah salah satu notasi umum untuk turunan. Definisi turunan ini mengandung hubungan yang intuitif bahwa suatu fungsi terdiferensialkan f bersifat menaik jika dan hanya jika turunannya bernilai positif, dan menurun jika dan hanya jika turunannya bernilai negatif. Fakta ini sering digunakan dalam analisis mengenai perilaku fungsi, contohnya dalam menentukan titik ekstrem fungsi.
Selain itu, turunan juga memenuhi sifat
yang menghasilkan interpretasi yang intuitif (lihat Gambar 1) bahwa garis singgung fungsi f di a memberikan hampiran linear terbaik
untuk nilai fungsi f di sekitar a (yakni, untuk nilai h yang kecil). Interpretasi ini adalah konsep termudah yang dapat diperumum ke kasus-kasus lainnya.
Metode subtitusi h dengan nol pada perbandingan beda tidak dapat dilakukan karena menghasilkan pembagian oleh nol. Hal ini menyebabkan besar kemiringan dari garis singgung tidak dapat ditemukan secara langsung lewat subtitusi. Besar kemiringan dapat ditentukan mendefinisikan Q(h) menjadi perbandingan (quotinent) beda sebagai fungsi dari h:
secara geometris menyatakan kemiringan dari garis sekan yang melalui dan . Jika f adalah fungsi kontinu, secara informal mengartikan grafik fungsinya berupa kurva tak putus dan tidak mengandung celah, maka fungsi Q kontinu selain di . Jika limit ada, maka ada cara lain memilih nilai untuk Q(0) yang membuat Q menjadi fungsi kontinu, membuat fungsi f terdiferensialkan di a, dan besar turunannya di a sama dengan Q(0). Pada praktiknya, keberadaan Q(h) yang kontinu di ditunjukkan dengan mengubah ekspresi pada pembilang agar dapat "mencoret" semua suku h pada penyebut. Manipulasi seperti itu memungkinkan nilai limit dari Q untuk nilai h yang kecil terlihat jelas, walaupun Q masih tidak terdefinisi di . Proses manipulasi ini dapat sangat panjang dan melelahkan untuk fungsi yang rumit, dan banyak jalan pintas digunakan untuk menyederhanakan proses.
Contoh perhitungan[sunting | sunting sumber]

Fungsi kuadrat memiliki persamaan f(x) = x2 dan diferensialkan di x = 3, dengan nilai turunan fungsi di titik tersebut adalah 6. Hasil ini didapatkan dari menghitung limit dengan h menuju nol, dari persamaan beda f(3):
Sejarah[sunting | sunting sumber]
Kalkulus, atau dikenal dalam sejarah lebih awalnya, kalkulus infinitesimal, merupakan cabang matematika yang berfokus pada konsep limit, fungsi, turunan, integral, dan deret takhingga. Isaac Newton dan Gottfried Leibniz menemukan kalkulus secara terpisah pada pertengahan abad ke-17. Namun dalam pertikaian yang pahit, Leibniz dituduh bahwa ia mencuri karya Newton dan sebaliknya. Pertikaian ini berlanjut hingga kematian mereka berdua.
Definisi[sunting | sunting sumber]
Sebuah fungsi dengan variabel real, , dikatakan terdiferensialkan atau dapat diturunkan pada suatu titik di domainnya, jika domain fungsi tersebut mengandung suatu interval buka yang beranggotakan , dan nilai limit
Jika fungsi terdiferensialkan di , dengan kata lain jika nilai limit ada, maka nilai limit ini disebut turunan dari di , dan dinyatakan dengan atau (dibaca "turunan dari terhadap di " atau "dy per dx di ").
Kekontinuan dan keterdiferensialan[sunting | sunting sumber]

Fungsi yang terdiferensialkan di suatu titik , juga akan bersifat kontinu di titik tersebut. Sebagai contoh dari sifat ini, misalkan f adalah fungsi tangga yang menghasilkan nilai 1 untuk semua x kurang dari nilai a, dan menghasilkan nilai yang berbeda, misalnya 10, untuk semua nilai x yang lebih besar atau sama dengan a. Fungsi f tidak dapat memiliki turunan di titik a. Untuk nilai h yang negatif, titik a + h akan terletak di sisi rendah dari fungsi tangga, menjadikan garis sekan dari a ke a + h akan sangat curam; dan semakin curam saat h menuju nol. Sedangkan nilai h yang positif, maka a + h terletak pada sisi tinggi dari fungsi tangga, sehingga garis sekan dari a ke a + h tidak memiliki kemiringan (datar). Alhasil garis-garis sekan tidak menuju besar kemiringan yang sama, mengakibatkan nilai limit dari persamaan beda tidak ada.

Tetapi, bahkan jika fungsi kontinu di suatu titik, fungsi tersebut mungkin tidak terdiferensialkan di sana. Sebagai contoh, fungsi nilai mutlak f(x) = |x| bersifat kontinu di x = 0, namun tidak terdiferensialkan di titik itu. Jika h positif, maka kemiringan dari garis sekan dari 0 ke h bernilai 1, sedangkan jika h negatif, maka kemiringan garis sekan dari 0 ke h bernilai -1. Bahkan fungsi mulus tidak dapat diturunkan di titik yang garis singgungnya merupakan garis vertikal: Sebagai contoh, fungsi f(x) = x1/3 tidak terdiferensialkan di x = 0.
Secara singkat, fungsi yang terdiferensialkan adalah fungsi yang kontinu, tetapi ada fungsi kontinu yang tidak dapat didiferensialkan.
Sebagian besar fungsi pada praktiknya memiliki turunan di semua titik atau hampir semua titik. Pada awal sejarah kalkulus, banyak matematikawan mengasumsikan fungsi kontinu dapat diturunkan di banyak titik. Pada kondisi yang standar, hal ini berlaku karena kebanyakan fungsi adalah fungsi monoton atau fungsi Lipschitz. Tetapi pada tahun 1872, Weierstrass menemukan contoh pertama dari fungsi yang kontinu dimanapun namun tidak terdiferensialkan dimanapun. Contoh tersebut sekarang dikenal sebagai fungsi Weierstrass.
Turunan sebagai sebuah fungsi[sunting | sunting sumber]

Misalkan f adalah fungsi yang memiliki turunan di setiap titik di domainnya. Seseorang dapat mendefinisikan sebuah fungsi yang memetakan setiap titik x ke nilai dari turunan f di x. Salah satu notasi untuk menulis fungsi ini adalah , dan disebut sebagai fungsi turunan atau turunan dari f. Terkadang f memiliki turunan pada sebagian besar, tapi tidak semua, titik di domainnya. Fungsi yang nilainya di a sama dengan kapanpun nilai terdefinisi, dan tidak terdefinisi di nilai-nilai yang lainnya, juga disebut turunan dari f. Fungsi ini memiliki domain yang lebih kecil daripada domain dari f.
Menggunakan ide tersebut, turunan dapat dianggap sebagai fungsi dari fungsi: Turunan adalah sebuah operator dengan domainnya adalah himpunan semua fungsi yang memiliki turunan di semua titik pada domain mereka, dan citra-nya (range) adalah himpunan berisi fungsi-fungsi. Jika operator ini dinyatakan dengan D, maka D(f) sama dengan fungsi . Selain itu, karena D(f) adalah sebuah fungsi, nilainya dapat dihitung di titik a. Dengan menggunakan definisi dari fungsi turunan,
Sebagai contoh, pertimbangkan fungsi f(x) = 2x; f adalah fungsi satu variabel yang bernilai real, mengartikan fungsi ini menerima sebuah angka lalu menghasilkan sebuah angka:
Operator D di sisi lain, tidak menerima maupun menghasilkan angka, melainkan fungsi:
Karena D menghasilkan sebuah fungsi, hasil dari D dapat dievaluasi di suatu titik. Sebagai contoh, ketika D diterapkan pada fungsi kuadrat x ↦ x2, D akan menghasilkan fungsi x ↦ 2x, yang dapat diberi nama f(x). Fungsi hasil ini selanjutnya dapat digunakan untuk menghitung f(1) = 2, f(2) = 4, dan seterusnya.
Notasi turunan[sunting | sunting sumber]
Beberapa notasi untuk menyatakan turunan dikembangkan pada awal perkembangan kalkulus, dan beberapa notasi tersebut masih digunakan saat ini.
Notasi Leibniz[sunting | sunting sumber]

Simbol , , dan diperkenalkan oleh Gottfried Wilhelm Leibniz pada tahun 1675.[2] Notasi ini masih umum digunakan ketika persamaan ingin dipandang sebagai hubungan antara variabel terikat dan variabel bebas. Turunan pertama dengan notasi ini ditulis sebagai
Dengan menggunakan notasi Leibniz, turunan dari di titik dapat ditulis dalam dua cara berbeda:
Notasi Leibniz memungkinkan penulisan variabel diferensiasi (sebagai penyebut), yang berperan dalam turunan parsial. Notasi ini juga dapat digunakan untuk menulis aturan rantai sebagai[Note 1]
Selain itu, notasi Leibniz memperlihatkan hubungan variabel yang sesuai dengan analisis dimensi. Sebagai contoh, turunan kedua memiliki dimensi yang sama dengan .
Notasi Lagrange[sunting | sunting sumber]
Terkadang disebut dengan notasi petik/prima (prime notation),[4] salah satu notasi turunan yang umum lainnya adalah notasi yang diperkenalkan Joseph-Louis Lagrange. Notasi ini menggunakan simbol prima, yang mirip dengan simbol petik. Turunan dari fungsi dituliskan sebagai . Serupa dengan itu, turunan kedua dan ketiga dari fungsi ditulis sebagai
- dan
Untuk menyatakan turunan tingkat tinggi, beberapa penulis menggunakan angka Romawi yang ditulis sebagai tika atas, sedangkan yang lain menuliskan angka dalam simbol kurung:
- atau
Notasi yang kedua dapat diperumum untuk menghasilkan notasi untuk turunan ke-n dari . Notasi ini ringkas dan paling berguna ketika turunan dianggap sebagai fungsi tersendiri, berbeda dengan notasi Leibniz yang mengganggap turunan sebagai hubungan antar variabel. Nilai fungsi turunan ke-n di dituliskan sebagai .
Notasi Newton[sunting | sunting sumber]
Notasi Newton untuk turunan juga disebut sebagai notasi dot/titik. Notasi ini menggunakan titik yang diletakkan di atas nama fungsi, untuk merepresentasikan turunan terhadap waktu. Jika , maka
- dan
masing-masing menyatakan turunan pertama dan turunan kedua dari . Notasi Newton saat ini hanya digunakan untuk turunan terhadap waktu atau terhadap panjang busur, yang umum ditemukan dalam persamaan diferensial di fisika dan geometri diferensial.[5][6] Notasi Newton, malangnya, sulit digunakan untuk turunan tingkat tinggi (turunan ke-4 atau lebih), dan tidak dapat digunakan untuk fungsi multivariabel.
Notasi Euler[sunting | sunting sumber]
Notasi yang diperkenalkan Leonhard Euler menggunakan operator diferensial , yang ketika diterapkan pada sebuah fungsi akan menghasilkan turunan pertama . Turunan ke-n dengan notasi ini ditulis sebagai . Jika adalah variabel terikat, maka tika bawah umum dilekatkan ke untuk memperjelas adalah variabel bebas. Notasi Euler selanjutnya dapat ditulis sebagai
- atau ,
walaupun tika bawah umumnya tidak digunakan jika konteks variabel dapat dipahami, contohnya ketika adalah satu-satunya variabel bebas dalam ekspresi. Notasi Euler berguna dalam menyatakan dan menyelesaikan sistem persamaan diferensial linear.
Kaidah dalam menentukan turunan fungsi[sunting | sunting sumber]
Definisi turunan dapat digunakan untuk menentukan turunan suatu fungsi, seperti dan . Proses ini dilakukan membuat persamaan perbandingan beda, lalu menghitung limitnya. Tapi pada praktiknya proses ini seringkali melelahkan. Dalam pendidikan terkait kalkulus diferensial, proses ini hanya dilakukan pada awal pembelajaran. Selanjutnya, menentukan turunan fungsi dilakukan dengan merujuk pada tabel/daftar turunan fungsi yang umum maupun dengan menggunakan aturan-aturan turunan.
Kaidah untuk fungsi-fungsi dasar[sunting | sunting sumber]
Setiap aturan pada bagian ini dapat dihasilkan dengan membuat persamaan beda, lalu menghitung limit . Proses tersebut memerlukan strategi yang berbeda untuk mendapatkan hasil turunan, tergantung jenis fungsinya. Pada bagian ini, berupa bilangan real.
Contoh 1: mencari turunan dy/dx dari:
dapat dilakukan dengan cara berikut:
Contoh 2: mencari turunan dx/dy dari:
dapat dilakukan dengan cara berikut:
- Fungsi eksponensial dan logaritma:
- Fungsi trigonometri:
- Fungsi invers trigonometri:
Kaidah untuk fungsi komposit[sunting | sunting sumber]
Beberapa aturan berikut dapat digunakan untuk menentukan turunan komposisi fungsi dengan membaginya menjadi masalah-masalah turunan yang lebih sederhana. Pada bagian ini, , , dan adalah fungsi yang terdiferensialkan pada selang .
- Aturan konstanta:
- untuk berupa fungsi konstan.
- Kaidah jumlah:
- untuk semua fungsi f dan g, dan untuk semua bilangan real dan .
- Kaidah darab:
- untuk semua fungsi f dan g. Aturan ini mencakup kasus yang istimewa, yakni fakta bahwa dengan berupa konstanta. Karena menurut aturan konstanta, .
- Kaidah hasil-bagi:
- untuk semua fungsi dan , di semua titik di yang memenuhi . Pada kasus berupa fungsi konstan bernilai , akan didapatkan hubungan
- Aturan rantai untuk komposisi fungsi:
- Jika fungsi terdiferensialkan pada selang , dan fungsi terdiferensialkan pada selang ( adalah citra dari yang dihasilkan fungsi ), maka komposisi fungsi terdiferensialkan di dan
- Kaidah fungsi invers:
- Jika fungsi bersifat bijektif, dan adalah invers dari fungsi tersebut, maka
- Hubungan ini berlaku sembarang titik yang memenuhi
Contoh perhitungan[sunting | sunting sumber]
Turunan dari fungsi
dapat dilakukan dengan pertama kali menerapkan kaidah jumlah; turunan dari penjumlahan fungsi-fungsi sama dengan penjumlahan dari turunan fungsi-fungsi:
Turunan tingkat tinggi[sunting | sunting sumber]
Misalkan adalah fungsi terdiferensialkan, dan adalah fungsi turunannya. Turunan dari (jika ada) ditulis sebagai dan disebut turunan kedua dari . Serupa dengan itu, turunan dari turunan kedua, jika ada, ditulis sebagai dan disebut turunan ketiga dari ; dan seterusnya. Turunan berulang ini disebut turunan tingkat tinggi. Turunan ke-n juga dapat dituliskan sebagai . Jika menyatakan posisi suatu objek pada waktu , maka turunan tingkat tinggi dari memiliki interpretasi khusus dalam bidang fisika. Turunan pertama dari menyatakan kecepatan objek, turunan kedua menyatakan besar akselerasinya, sedangkan turunan ketiga dari menyatakan sentakan.
Fungsi mulus[sunting | sunting sumber]
Sebuah fungsi yang dapat diturunkan tak hingga kali disebut fungsi mulus. Tidak semua fungsi merupakan fungsi mulus; sebagai contoh, fungsi yang tidak kontinu tidak dapat diturunkan. Serupa dengan itu, bahkan jika memiliki turunan, fungsi turunan keduanya mungkin tidak ada. Sebagai contoh, misalkan fungsi
Perhitungan menunjukkan bahwa adalah fungsi yang terdiferensialkan namun tidak memiliki turunan di nol. Jika suatu fungsi dapat diturunkan k kali berturut-turut dan turunan ke-k-nya bersifat kontinu, maka fungsi tersebut merupakan anggota kelas keterdiferensialan Ck.
Polinomial Taylor dengan sisa[sunting | sunting sumber]
Pada garis bilangan real, setiap fungsi polinomial terdiferensialkan tak hingga kali. Dengan menggunakan kaidah turunan pangkat, sebuah polinomial berderajat n akan menjadi fungsi konstan jika diturunkan sebanyak n kali. Semua turunan fungsi tersebut selanjutnya sama dengan 0 (fungsi konstan). Hal ini mengartikan fungsi polinomial termasuk fungsi mulus.
Turunan tingkat tinggi dari sebuah fungsi di suatu titik , akan memberikan hampiran polinomial terbaik untuk fungsi tersebut di sekitar titik . Sebagai contoh, jika terdiferensialkan dua kali, maka
dalam artian bahwa
Jika terdiferensialkan tak hingga kali, maka persamaan turunan kedua dapat diteruskan menjadi deret Taylor untuk fungsi yang dievaluasi di x + h sekitar titik x.
Kaidah untuk turunan tingkat tinggi[sunting | sunting sumber]
- Aturan Leibniz
- Jika dan dapat diturunkan sebanyak kali, maka turunan ke- dari fungsi adalah
- Ekspresi yang muncul pada persamaan tersebut menandakan koefisien binomial. Aturan ini adalah perumuman dari kaidah darab.
Turunan pada sistem bilangan kompleks[sunting | sunting sumber]
Definisi dan aturan-aturan terkait turunan dapat diperumum untuk fungsi dengan variabel kompleks dan nilai kompleks. Perumuman ini dapat dilakukan karena bilangan kompleks juga memiliki sifat penjumlahan, perkalian, dan pembagian; sama seperti bilangan real. Selain itu, konsep jarak (Euklides) antar bilangan pada bilangan kompleks dapat dijelaskan secara sederhana.
Jika berupa himpunan buka, dan adalah fungsi bernilai kompleks, maka dikatakan terdiferensialkan di titik bila nilai limit
ada.[8] Turunan kompleks ini disimbolkan dengan Definisi ini memungkinkan untuk menggunakan konsep kelinearan: turunan menyatakan besar "kemiringan" dari fungsi [kompleks] linear terbaik yang menghampiri fungsi Tapi, perhatian lebih diperlukan karena nilai pada limit berupa bilangan kompleks. Berbeda dengan limit pada bilangan real yang hanya memerlukan dua arah ("limit dari kanan" dan "limit dari kiri"), limit pada bilangan kompleks dapat "bergerak" dari takhingga banyaknya arah. Akibatnya, konsep turunan fungsi kompleks jauh lebih ketat ketimbang pada fungsi bernilai real. Sebagai contoh fungsi nilai mutlak kompleks tidak memiliki turunan dimanapun. Sebuah fungsi kompleks dapat diturunkan pada suatu titik, jika dan hanya jika fungsi tersebut memenuhi persamaan Cauchy-Riemann di titik tersebut.
Walaupun (atau tepatnya karena) konsep turunan yang jauh lebih ketat, aturan-aturan perhitungan turunan pada fungsi bilangan real dapat digunakan untuk fungsi bilangan kompleks. Hal ini mencakup aturan jumlah, darab, dan rantai, juga aturan fungsi invers. Banyak fungsi kompleks, seperti eksponensial dan logaritma, memiliki sifat turunan yang mirip dengan versi realnya.
Jika fungsi terdiferensialkan di keseluruhan domain , maka fungsi disebut fungsi holomorfik di .[9] Fungsi kompleks yang terdiferensialkan di keseluruhan disebut fungsi entire. Fungsi holomorfik memiliki beberapa sifat yang unik. Sebagai contoh, teorema Picard menyimpulkan bahwa citra (range) dari fungsi entire hanya dapat berupa: , , atau untuk suatu . Hasil ini dapat digunakan untuk menyimpulkan bahwa, jika fungsi kompleks tidak pernah menghasilkan nilai maupun nilai , maka adalah fungsi konstan.
Turunan untuk fungsi bernilai vektor[sunting | sunting sumber]

Sebuah fungsi bernilai vektor dengan variabel real, adalah fungsi yang memetakan bilangan real (ril) ke suatu vektor di suatu ruang vektor . Fungsi bernilai vektor dapat dibagi menjadi fungsi-fungsi koordinatnya, . Hal ini mengartikan fungsi dapat ditulis sebagai . Contoh dari fungsi bernilai vektor adalah kurva parametrik di atau . Fungsi-fungsi koordinat adalah fungsi bernilai real, mengakibatkan definisi turunan dapat diterapkan bagi mereka semua. Turunan dari fungsi didefinisikan sebagai sebuah vektor, disebut vektor singgung, yang koordinatnya adalah nilai turunan dari semua fungsi koordinatnya. Dengan kata lain,
Turunan untuk fungsi multivariabel[sunting | sunting sumber]
Pembahasan pada bagian-bagian sebelumnya hanya memperhatikan fungsi dengan satu variabel. Fungsi yang memetakan vektor ke vektor maupun vektor ke bilangan juga dapat memiliki turunan. Tetapi, garis singgung pada grafik fungsi tersebut belum tentu unik, karena ada banyak arah yang mungkin untuk membuat garis tersebut. Oleh karena itu, perumuman turunan diperlukan untuk jenis fungsi ini.
Keterdiferensialan dan matriks Jacobi[sunting | sunting sumber]
Turunan parsial[sunting | sunting sumber]
Misalkan adalah fungsi multivariabel, sebagai contoh Fungsi dapat dianggap sebagai keluarga fungsi satu variabel yang diindeks oleh variabel-variabel yang lain:
Dalam contoh ini, setiap nilai akan menghasilkan sebuah fungsi yang merupakan fungsi satu variabel. Hal ini dapat dinyatakan dengan pemetaan
Setelah suatu nilai dipilih, misalnya , maka selanjutnya menentukan sebuah fungsi yang memetakan ke , juga dapat ditulis sebagai . Dalam ekspresi tersebut adalah sebuah konstanta dan bukan sebuah variabel, menjadikan sebagai fungsi satu variabel. Alhasil, definisi turunan untuk fungsi satu variabel berlaku:
Prosedur ini dapat diterapkan untuk sembarang pemilihan nilai . Menggunakan notasi Leibniz, turunan ini menyampaikan perbandingan perubahan nilai fungsi dalam arah :
dan disebut sebagai turunan berarah dari terhadap . Dalam ekspresi tersebut, simbol ∂ adalah huruf d melengkung yang disebut sebagai simbol turunan parsial. Untuk membedakannya dengan huruf d yang digunakan dalam turunan satu variabel, ∂ terkadang dilafalkan sebagai "der", "del", atau "parsial", ketimbang "de".
Secara umum, turunan parsial sebuah fungsi dalam arah di titik didefinisikan sebagai
Dalam perbandingan beda di atas, semua nilai variabel kecuali dibuat konstan. Tindakan membuat konstan variabel-variabel ini akan menghasilkan fungsi satu variabel
dan dari definisi,
Ekspresi ini juga menunjukkan bahwa perhitungan turunan parsial dapat disederhanakan menjadi perhitungan turunan satu variabel.
Turunan parsial juga memainkan peran penting dalam pembahasan terkait fungsi bernilai vektor. Misalkan sebagai fungsi bernilai vektor. Jika semua turunan parsial terdefinisi di titik , turunan-turunan parsial ini mendefinisikan sebuah vektor
yang disebut sebagai gradien dari di . Jika terdiferensialkan di setiap titik di suatu domain, maka gradien adalah sebuah fungsi bernilai vektor yang memetakan titik ke vektor . Akibatnya, gradien menentukan suatu medan vektor.
Turunan berarah[sunting | sunting sumber]

Jika adalah fungsi bernilai real di , maka turunan parsial mengukur variasi turunan dalam arah sumbu koordinat. Sebagai contoh, jika adalah fungsi dari dan , maka turunan parsial mengukur variasi di dalam arah dan . Tapi, turunan tidak mengukur secara langsung variasi pada setiap arah lainnya, contohnya di sepanjang garis diagonal . Ini diukur menggunakan turunan berarah. Misalkan vektor
turunan berarah dalam arah di titik x didefinisikan melalui limit
Dalam beberapa kasus, menghitung atau menaksir turunan berarah akan lebih mudah setelah panjang vektor diubah. Proses ini seringkali dilakukan dengan mengubah suatu masalah menjadi perhitungan berupa turunan berarah dalam arah satuan vektor. Sebagai contoh, misalkan dan adalah satuan vektor pada arah . Mensubstitusi ke perbandingan beda di ruas kanan persamaan, akan menghasilkan bentuk
Dengan mengambil limit menuju nol dari persamaan di atas, didapatkan hubungan turunan berarah dalam arah vektor sama saja dengan kali turunan berarah dalam arah vektor satuan . Oleh karena itu, . Karena sifat penskalaan ini, turunan berarah seringkali digunakan hanya untuk vektor satuan.
Jika semua turunan parsial ada dan kontinu di , maka semua turunan parsial menentukan turunan berarah pada arah melalui rumus berikut:
Rumus di atas merupakan akibat dari definisi turunan total. Rumus ini juga menunjukkan bahwa turunan berarah bersifat linear di , dalam artian .
Definisi yang sama juga berlaku ketika berupa fungsi yang memiliki nilai di ; dengan menerapkan definisi pada setiap komponen vektor. Pada kasus ini, turunan berarah merupakan vektor di .
Diferensial total dan matriks Jacobi[sunting | sunting sumber]
Jika merupakan sebuah fungsi dari himpunan terbuka dari ke , maka turunan berarah dalam arah yang dipilih merupakan hampiran linear terbaik ke di titik dan arah tersebut. Tetapi jika , maka tidak ada turunan berarah tunggal yang dapat memberikan gambaran lengkap mengenai perilaku fungsi . Turunan total memberikan gambaran lengkap dengan meninjau semua arah sekaligus. Dalam artian, untuk suatu vektor yang dimulai dari , terdapat rumus hampiran linear yang berlaku sebagai:
Sama seperti turunan satu variabel, dipilih sehingga galat hampiran tersebut dapat dibuat sekecil mungkin.
Jika dan bernilai 1, maka turunan merupakan sebuah nilai dan bentuk merupakan hasil kali dari dua bilangan. Tetapi dalam dimensi yang lebih tinggi, tidak dapat berupa sebuah bilangan. Jika adalah sebuah bilangan, maka akan berupa vektor di . Sedangkan bentuk-bentuk lainnya berupa vektor di sehingga rumus hampiran linear menjadi tidak masuk akal. Agar rumus hampiran linear menjadi masuk akal, harus sebuah fungsi yang memetakan vektor di ke vektor di , dan harus menyatakan fungsinya dapat dihitung di .
Untuk menentukan jenis fungsi apakah tersebut, perhatikan bahwa rumus hampiran linear dapat ditulis ulang sebagai
Perhatikan bahwa jika vektor lain dipilih, katakanlah , maka persamaan hampiran tersebut menentukan persamaan hampiran lain dengan memasukkan ke . Ini menentukan persamaan aproksimasi ketiga dengan memasukan nilai ke dan ke . Dengan mengurangi kedua persamaan tersebut akan mendapatkan persamaan berikut.
Jika diasumsikan bahwa bernilai kecil dan bahwa perubahan turunan kontinu di , maka kira-kira sama dengan . Karena itu, ruas kanan pada persamaan tersebut kira-kira sama dengan nol. Ruas kiri pada persamaan dapat ditulis ulang dalam cara yang berbeda dengan menggunakan rumus hampiran linear, dengan dimasukkan . Rumus hampiran linear menyiratkan:
Rumus tersebut menyarankan bahwa merupakan transformasi linear dari ruang vektor ke ruang vektor . Bahkan rumus ini dapat membuat sebuah turunan yang tepat dengan mengukur galat pada hampirannya. Asumsi bahwa galat pada rumus hampiran linear dibatasi oleh hasil kali dari konstanta dengan , dengan konstantanya bebas dari namun kontinu bergantung pada . Setelah menambahkan sebuah bentuk galat yang sesuai, maka semua persamaan hampiran di atas dapat ditulis ulang sebagai pertidaksamaan. Khususnya, merupakan sebuah transformasi linear hingga bentuk galat kecil. Dalam limit, ketika dan menuju ke nol, harus berupa transformasi linear. Karena turunan total didefinisikan dengan mengambil limit ketika menuju ke nol, harus berupa transformasi linear.
Kaidah untuk turunan fungsi multivariabel[sunting | sunting sumber]
Turunan implisit[sunting | sunting sumber]
Contoh penerapan[sunting | sunting sumber]
Turunan pada sistem bilangan hiperreal[sunting | sunting sumber]
Dalam matematika, bilangan hiperreal adalah sebuah cara memaknai besaran tak hingga dan infinitesimal (tak hingga kecilnya tapi tidak nol). Hiperreal adalah perumuman dari himpunan bilangan real , dan mencakup bilangan-bilangan yang lebih besar daripada (untuk sembarang terhingga banyaknya suku). Pada sistem bilangan ini, turunan fungsi real di titik real dapat didefinisikan sebagai bayangan perbandingan ∆y∆x untuk infinitesimal ∆x, dengan ∆y = f(x + ∆x) − f(x). Perluasan (perumuman, ekstensi) alami fungsi untuk hiperreal masih dilambangkan sebagai , dan turunannya dikatakan ada jika besar bayangan tidak bergantung pada pemilihan infinitesimal.
Perumuman[sunting | sunting sumber]
Konsep turunan dapat diperluas menjadi perumuman lainnya. Kaitan yang paling umumnya adalah turunan fungsi di sebuah titik disajikan sebagai hampiran linear dari fungsi pada titik tersebut.
- Perumuman penting mengenai turunan melibatkan fungsi kompleks dari variabel kompleks, seperti fungsi (dengan domain) bilangan kompleks ke . Gagasan turunan fungsi kompleks diperoleh dengan menggantikan variabel real dengan variabel kompleks melalui definisi berikut: Jika diidentifikasi sebagai dengan menulis bilangan kompleks sebagai , maka sebuah fungsi terdiferensialkan dari ke pasti terdiferensialkan sebagai sebuah fungsi dari ke (dalam artian bahwa semua turunan parsial juga ada), tetapi kebalikannya tidak benar pada umumnya: turunan kompleks hanya ada jika turunan real merupakan linear kompleks dan turunan kompleks memaksakan kaitannya antara turunan parsial yang disebut sebagai persamaan Cauchy–Riemann – lihat fungsi holomorfik.
- Perumuman lainnya melibatkan fungsi antara manifold terdiferensialkan atau manifold mulus. Secara intuitif, manifold dikatakan sebagai ruang yang dapat dihampiri mendekati setiap titik melalui sebuah ruang vektor yang disebut sebagai ruang garis singgung: contoh prototipikalnya adalah permukaan mulus di . Turunan (atau diferensial) dari peta (terdiferensialkan) di antara manifold, di sebuah titik di , merupakan peta linear dari ruang singgung di ke ruang singgung di , sehingga turunan fungsi menjadi sebuah peta antara berkas garis singgung dan . Definisi tersebut merupakan bentuk dasar dalam geometri diferensial, dan definisi tersebut mempunyai banyak kegunaan – lihat pushforward dan pullback.
- Diferensiasi juga dapat didefinisikan sebagai pemetaan antara ruang vektor dimensi takhingga, seperti ruang Banach dan ruang Fréchet. Perumuman dari turunan berarah disebut turunan Gateaux, dan perumuman dari diferensial disebut turunan Fréchet.
- Salah satu kekurangan turunan biasa adalah bahwa ada sangat banyak sekali fungsi yang tidak terdiferensialkan. Namun ada cara memperluas gagasan turunan sehingga semua fungsi kontinu dan fungsi lainnya dapat diturunkan melalui konsep yang dikenal sebagai turunan lemah. Tujuannya adalah agar memasukkan fungsi kontinu dalam sebuah ruang yang lebih besar yang disebut ruang distribusi, dan tujuan ini hanya mengharuskan bahwa fungsi "rata-rata" terdiferensialkan.
- Pengenalan dan studi mengenai banyak topik yang serupa dalam aljabar dan topologi diilhami melalui sifat-sifat turunan — sebagai contoh, lihat aljabar diferensial.
- Definisi turunan yang ekuivalen diskret adalah beda hingga. Dalam kalkulus skala waktu, studi mengenai kalkulus diferensial disatukan dengan kalkulus beda hingga.
Lihat pula[sunting | sunting sumber]
- Analisis matematis
- Aturan pendiferensialan
- Diferintegral
- Generalisasi turunan
- Integral
- Infinitesimal
- Invers perkalian
- Kelajuan (mathematika)
- Kelas keterdiferensialan
- Linearisasi
- Pendiferensialan numerik
- Pendiferensialan otomatik
- Penerapan turunan
- Sejarah kalkulus
- Teorema Radon–Nikodym
- Turunan aritmetika
- Turunan fraktal
- Turunan Hasse
- Turunan Schwarz
- Turunan simetrik
Catatan kaki[sunting | sunting sumber]
- ^ Dalam formulasi kalkulus menggunakan konsep limit, simbol du digunakan untuk menyatakan banyak hal oleh banyak penulis. Beberapa penulis tidak memandang du tidak memiliki makna tersendiri, dan hanya terdefinisi sebagai bagian dari simbol du/dx. Penulis yang lain mendefinisikan dx sebagai variabel bebas, dan du' sebagai . Dalam analisis non-standar, du didefinisikan sebagai suatu infinitesimal, dan juga dapat dipandang sebagai turunan eksterior dari fungsi u. Lihat diferensial (matematika) untuk informasi lebih lanjut.
Referensi[sunting | sunting sumber]
- ^ Spivak 1994, chapter 10.
- ^ Manuscript of November 11, 1675 (Cajori vol. 2, page 204)
- ^ Perhatikan bahwa adalah notasi ringkas untuk , atau, dalam kata lain diferensial kedua dari y terhadap kuadrat dari diferensial pertama dari x. Penyebut bukanlah diferensial dari x2, atau diferensial kedua dari x.
- ^ "The Notation of Differentiation". MIT. 1998. Diakses tanggal 24 October 2012.
- ^ Evans, Lawrence (1999). Partial Differential Equations. American Mathematical Society. hlm. 63. ISBN 0-8218-0772-2.
- ^ Kreyszig, Erwin (1991). Differential Geometry. New York: Dover. hlm. 1. ISBN 0-486-66721-9.
- ^ "3.4: Implicit Differentiation". Mathematics LibreTexts (dalam bahasa Inggris). 2021-01-02. Diakses tanggal 2022-11-05.
- ^ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 35.
- ^ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 45.
Daftar pustaka[sunting | sunting sumber]
Buku cetak[sunting | sunting sumber]
- Anton, Howard; Bivens, Irl; Davis, Stephen (February 2, 2005), Calculus: Early Transcendentals Single and Multivariable (edisi ke-8th), New York: Wiley, ISBN 978-0-471-47244-5
- Apostol, Tom M. (June 1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra
 , 1 (edisi ke-2nd), Wiley, ISBN 978-0-471-00005-1
, 1 (edisi ke-2nd), Wiley, ISBN 978-0-471-00005-1 - Apostol, Tom M. (June 1969), Calculus, Vol. 2: Multi-Variable Calculus and Linear Algebra with Applications
 , 1 (edisi ke-2nd), Wiley, ISBN 978-0-471-00007-5
, 1 (edisi ke-2nd), Wiley, ISBN 978-0-471-00007-5 - Courant, Richard; John, Fritz (December 22, 1998), Introduction to Calculus and Analysis, Vol. 1, Springer-Verlag, ISBN 978-3-540-65058-4
- Eves, Howard (January 2, 1990), An Introduction to the History of Mathematics (edisi ke-6th), Brooks Cole, ISBN 978-0-03-029558-4
- Larson, Ron; Hostetler, Robert P.; Edwards, Bruce H. (February 28, 2006), Calculus: Early Transcendental Functions (edisi ke-4th), Houghton Mifflin Company, ISBN 978-0-618-60624-5
- Spivak, Michael (September 1994), Calculus (edisi ke-3rd), Publish or Perish, ISBN 978-0-914098-89-8
- Stewart, James (December 24, 2002), Calculus
 (edisi ke-5th), Brooks Cole, ISBN 978-0-534-39339-7
(edisi ke-5th), Brooks Cole, ISBN 978-0-534-39339-7 - Thompson, Silvanus P. (September 8, 1998), Calculus Made Easy (edisi ke-Revised, Updated, Expanded), New York: St. Martin's Press, ISBN 978-0-312-18548-0
Buku daring[sunting | sunting sumber]
| Sumber pustaka mengenai Turunan |
- Crowell, Benjamin (2017), Fundamentals of Calculus
- (Govt. of TN), TamilNadu Textbook Corporation (2006), Mathematics- vol.2 (PDF), diarsipkan dari versi asli (PDF) tanggal 2016-01-15, diakses tanggal 2014-11-29
- Garrett, Paul (2004), Notes on First-Year Calculus, University of Minnesota
- Hussain, Faraz (2006), Understanding Calculus
- Keisler, H. Jerome (2000), Elementary Calculus: An Approach Using Infinitesimals
- Mauch, Sean (2004), Unabridged Version of Sean's Applied Math Book, diarsipkan dari versi asli tanggal 2006-04-15
- Sloughter, Dan (2000), Difference Equations to Differential Equations
- Strang, Gilbert (1991), Calculus
- Stroyan, Keith D. (1997), A Brief Introduction to Infinitesimal Calculus
- Wikibooks, Calculus
Pranala luar[sunting | sunting sumber]
| Cari tahu mengenai Differentiation pada proyek-proyek Wikimedia lainnya: | |
| Definisi dan terjemahan dari Wiktionary | |
| Gambar dan media dari Commons | |
| Berita dari Wikinews | |
| Kutipan dari Wikiquote | |
| Teks sumber dari Wikisource | |
| Buku dari Wikibuku | |
- Hazewinkel, Michiel, ed. (2001) [1994], "Derivative", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
- Khan Academy: "Newton, Leibniz, and Usain Bolt"
- (Inggris) Weisstein, Eric W. "Derivative". MathWorld.
- Online Derivative Calculator from Wolfram Alpha.









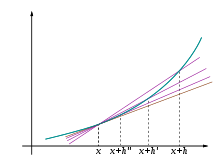














![{\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{\frac {f(3+h)-f(3)}{h}}=\lim _{h\to 0}{\frac {(3+h)^{2}-3^{2}}{h}}\\[10pt]&=\lim _{h\to 0}{\frac {9+6h+h^{2}-9}{h}}=\lim _{h\to 0}{\frac {6h+h^{2}}{h}}=\lim _{h\to 0}{(6+h)}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c937146572a5443c648de2852705afc883b35599)




![{\displaystyle {\begin{aligned}f'(a)&=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}=\lim _{h\to 0}{\frac {(a+h)^{2}-a^{2}}{h}}\\[0.3em]&=\lim _{h\to 0}{\frac {a^{2}+2ah+h^{2}-a^{2}}{h}}=\lim _{h\to 0}{\frac {2ah+h^{2}}{h}}\\[0.3em]&=\lim _{h\to 0}{(2a+h)}=2a\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/029b05dcc8c1a9d40e75bfcf806cbae45964b0b2)



























































































![{\displaystyle [f^{-1}]'(x)={\frac {1}{f'(f^{-1}(x))}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a2f012437b59b38b2b377b5fd87a19f6ac79ad9)













































































































