Integral
Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Integral di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: panduan penerjemahan artikel) |
| Kalkulus |
|---|

Integral adalah sebuah konsep penjumlahan secara berkesinambungan dalam matematika. Integral dan inversnya, diferensiasi, adalah operasi utama dalam kalkulus. Integral dikembangkan menyusul dikembangkannya masalah dalam diferensiasi, yaitu matematikawan harus berpikir bagaimana menyelesaikan masalah yang berkebalikan dengan solusi diferensiasi. Lambang integral adalah :
Bila diberikan suatu fungsi f dari variabel real x dengan interval [a, b] dari sebuah garis lurus, integral tertentu
didefinisikan sebagai area yang dibatasi oleh kurva f, sumbu-x, sumbu-y, serta garis vertikal x = a dan x = b dengan area yang berada di atas sumbu-x bernilai positif dan area di bawah sumbu-x bernilai negatif.
Kata integral juga dapat digunakan untuk merujuk pada antiturunan, sebuah fungsi F yang turunannya adalah fungsi f. Pada kasus ini, ia disebut sebagai integral tak tentu dan notasinya ditulis sebagai berikut.
Prinsip-prinsip dan teknik integrasi dikembangkan terpisah oleh Isaac Newton dan Gottfried Leibniz pada akhir abad ke-17. Melalui teorema fundamental kalkulus yang mereka kembangkan masing-masing, integral terhubung dengan diferensial: jika f adalah fungsi kontinu yang terdefinisi pada sebuah interval tertutup [a, b], jika antiturunan F dari f diketahui, integral tertentu dari f pada interval tersebut dapat didefinisikan sebagai:
Integral dan diferensial menjadi peranan penting dalam kalkulus dengan berbagai macam aplikasi pada sains dan teknik.
Terminologi dan notasi[sunting | sunting sumber]
Standar[sunting | sunting sumber]
Integral terhadap x dari fungsi nilai riil f dari variabel riil x pada interval [a, b] dapat ditulis sebagai[1][2][3]
Tanda integral ∫ mewakili integrasi. Simbol dx, disebut diferensial dari variabel x,[1] menunjukkan bahwa variabel integrasi adalah x. Fungsi dari f(x) untuk mengintegrasikan dapat disebut yaitu integran. Simbol dx dipisahkan dari integrand oleh spasi (seperti yang ditunjukkan). Suatu fungsi dikatakan dapat diintegralkan jika integral dari fungsi di atas domainnya berhingga. Intinya a dan b disebut batas integral. Suatu integral dimana batas ditentukan disebut integral pasti. Integral dikatakan melebihi interval [a, b].
Bila integral dipindahkan dari nilai terbatas a ke batas atas tak terhingga, integral menyatakan batas integral dari a menjadi nilai b karena b tak terhingga. Bila nilai integral semakin mendekati nilai berhingga, maka integral tersebut dikatakan dapat menyatu ke nilai tersebut. Jika tidak, integral dikatakan menyimpang.
Ketika batas dihilangkan, seperti pada
integral disebut integral tak tentu,[1][2] yang merepresentasikan kelas fungsi (antiturunan) yang turunannya adalah integran. Teorema dasar kalkulus menghubungkan evaluasi integral pasti ke integral tak tentu. Kadang-kadang, batas integrasi dihilangkan untuk integral tertentu ketika batas yang sama muncul berulang kali dalam konteks tertentu. Biasanya, penulis akan menjelaskan konvensi ini di awal teks yang relevan.
Ada beberapa ekstensi notasi integral untuk mencakup integrasi pada domain tak terbatas, dan atau dalam beberapa dimensi (lihat bagian selanjutnya dari artikel ini).
Arti simbol dx[sunting | sunting sumber]
Secara historis, simbol dx diambil untuk mewakili "bagian kecil" yang sangat kecil dari variabel independen x, yang akan dikalikan dengan integrand dan dijumlahkan dalam arti yang tak terbatas. Sedangkan pengertian ini masih berguna secara heuristik, matematikawan kemudian menganggap jumlah yang sangat kecil tidak dapat dipertahankan dari sudut pandang sistem bilangan riil.[4] Dalam kalkulus pengantar, ungkapan dx oleh karena itu tidak diberi arti yang independen; sebaliknya, ia dipandang sebagai bagian dari simbol integrasi dan berfungsi sebagai pembatasnya di sisi kanan ekspresi yang diintegrasikan.
Dalam konteks yang lebih canggih, dx dapat memiliki signifikansinya sendiri, artinya bergantung pada bidang matematika tertentu yang sedang dibahas. Saat digunakan dengan salah satu cara ini, notasi Leibnitz asli dipilih untuk diterapkan pada generalisasi definisi asli integral. Beberapa interpretasi umum dari dx termasuk: fungsi integrator dalam Integrasi Riemann-Stieltjes (ditunjukkan dengan dα (x) secara umum), a ukuran dalam teori Lebesgue (ditunjukkan dengan dμ secara umum), atau bentuk diferensial dalam kalkulus eksterior (ditunjukkan dengan secara umum). Dalam kasus terakhir, bahkan huruf d memiliki arti tersendiri sebagai operator turunan eksterior pada bentuk diferensial.
Sebaliknya, dalam pengaturan lanjutan, tidak jarang meninggalkan dx ketika hanya integral Riemann sederhana yang digunakan, atau jenis integral yang tepat tidak penting. Contohnya, seseorang mungkin menulis untuk mengungkapkan linearitas integral, properti yang dimiliki oleh integral Riemann dan semua generalisasinya.
Varian[sunting | sunting sumber]
Dalam notasi matematika Arab modern, simbol integral yang dipantulkan ![]() digunakan sebagai pengganti simbol ∫, karena skrip Arab dan ekspresi matematika dari kanan ke kiri.[5]
digunakan sebagai pengganti simbol ∫, karena skrip Arab dan ekspresi matematika dari kanan ke kiri.[5]
Beberapa penulis, terutama yang berasal dari Eropa, menggunakan "d" tegak untuk menunjukkan variabel integrasi (yaitu, dx alih-alih dx), karena berbicara dengan benar, "d" bukan bagian variabel.
Simbol dx tidak selalu ditempatkan setelah f(x), seperti misalnya di
Pada ekspresi pertama, diferensial diperlakukan sebagai faktor "perkalian" yang sangat kecil, secara formal mengikuti "properti komutatif" saat "dikalikan" dengan ekspresi tersebut 3/(x2+1). Pada ekspresi kedua, menunjukkan perbedaan pertama menyoroti dan mengklarifikasi variabel yang diintegrasikan terkait praktik yang sangat populer di kalangan fisikawan.
Sejarah[sunting | sunting sumber]
Integrasi pra-kalkulus[sunting | sunting sumber]
Teknik sistematis terdokumentasi pertama yang mampu menentukan integral adalah metode penghabis dari Yunani kuno astronom Eudoksos (ca. 370 SM), yang berusaha untuk menemukan luas dan volume dengan memecahnya menjadi beberapa divisi yang luas atau volumenya diketahui. Metode tersebut dikembangkan lebih lanjut dan digunakan oleh Archimedes pada abad ke-3 SM dan digunakan untuk menghitung luas lingkaran, luas permukaan dan volume bola, luas elips, luas di bawah parabola, volume segmen revolusi paraboloid, volume segmen hiperboloid revolusi, dan luas spiral.[6]
Metode serupa dikembangkan secara independen di Tiongkok sekitar abad ke-3 M oleh Liu Hui, yang menggunakan untuk mencari luas lingkaran. Metode ini kemudian digunakan pada abad ke-5 oleh ahli matematika ayah dan anak Tionghoa Zu Chongzhi dan Zu Geng untuk mencari volume bola (Shea 2007; Katz 2004, hlm. 125–126).
Di Timur Tengah, Hasan Ibn al-Haytham, dalam bahasa Latin sebagai Alhazen (c. 965 AD) menurunkan rumus untuk jumlah pangkat empat s. Dia menggunakan hasil untuk melakukan apa yang sekarang disebut integrasi fungsi ini, di mana rumus untuk jumlah kuadrat integral dan paraboloid.[7]
Kemajuan signifikan berikutnya dalam kalkulus integral baru mulai muncul pada abad ke-17. Pada saat ini, karya Cavalieri dengan metode Indivisibles miliknya, dan karya Fermat, mulai meletakkan dasar-dasar kalkulus modern, dengan Cavalieri menghitung integral dari xn dengan derajat nilai n = 9 dalam rumus kuadrat Cavalieri. Langkah selanjutnya dibuat pada awal abad ke-17 oleh Barrow dan Torricelli, yang memberikan petunjuk pertama tentang hubungan antara integrasi. Barrow memberikan bukti pertama dari teorema fundamental kalkulus. John Wallis menggeneralisasi metode Cavalieri, menghitung integral dari nilai x menjadi kekuatan umum, termasuk kekuatan negatif dan kekuatan pecahan.
Leibniz dan Newton[sunting | sunting sumber]
Kemajuan besar dalam integrasi terjadi pada abad ke-17 dengan penemuan independen dari teorema dasar kalkulus oleh Leibniz dan Newton. Leibniz menerbitkan karyanya tentang kalkulus sebelum Newton. Teorema menunjukkan hubungan antara integrasi dan diferensiasi. Hubungan tersebut, dikombinasikan dengan kemudahan pembedaan, dapat dimanfaatkan untuk menghitung integral. Secara khusus, teorema dasar kalkulus memungkinkan seseorang untuk memecahkan masalah kelas yang jauh lebih luas. Sama pentingnya adalah kerangka matematika komprehensif yang dikembangkan oleh Leibniz dan Newton. Diberikan nama kalkulus sangat kecil, tersebut memungkinkan untuk analisis fungsi yang tepat dalam domain kontinu. Kerangka ini akhirnya menjadi modern kalkulus, yang notasinya untuk integral diambil langsung dari karya Leibniz.
Formalisasi[sunting | sunting sumber]
Sementara Newton dan Leibniz memberikan pendekatan sistematis untuk integrasi, pekerjaan mereka tidak memiliki derajat rigor. Bishop Berkeley secara mengesankan menyerang langkah langkah yang digunakan Newton, memanggil mereka "hantu dari jumlah yang telah pergi". Kalkulus memperoleh pijakan yang lebih kokoh dengan pengembangan limit. Integrasi pertama kali diformalkan secara ketat, menggunakan batasan, oleh Riemann. Meskipun semua fungsi kontinu bagian yang dibatasi adalah Riemann-integrable pada interval yang dibatasi, selanjutnya fungsi yang lebih umum dipertimbangkan terutama dalam konteks analisis Fourier yang mendefinisikan Riemann tidak berlaku, dan Lebesgue merumuskan definisi integral yang berbeda, didirikan di teori ukuran (subbidang dari analisis nyata). Definisi integral lainnya, memperluas pendekatan Riemann dan Lebesgue, telah diusulkan. Pendekatan ini berdasarkan sistem bilangan real adalah yang paling umum saat ini, tetapi ada pendekatan alternatif, seperti definisi integral sebagai bagian standar dari jumlah Riemann tak terbatas, berdasarkan sistem bilangan hiperreal.
Notasi sejarah[sunting | sunting sumber]
Notasi untuk integral tak tentu diperkenalkan oleh Gottfried Wilhelm Leibniz pada tahun 1675 (Burton 1988, p. 359; Leibniz 1899, p. 154). Dia mengadaptasi simbol integral, ∫, dari lambang berbentuk ſ, singkatan dari summa (ditulis sebagai ſumma; dari Bahasa Latin "sum" atau "total"). Notasi modern untuk integral pasti, dengan batas di atas dan di bawah integral, pertama kali digunakan oleh Joseph Fourier Mémoires dari Akademi Prancis sekitar tahun 1819–2020, dicetak ulang dalam bukunya tahun 1822 (Cajori 1929, pp. 249–250; Fourier 1822, §231).
Isaac Newton menggunakan batang vertikal kecil di atas variabel untuk menunjukkan integrasi, atau menempatkan variabel di dalam kotak. Bilah vertikal mudah dikacaukan pada nilai atau x′, yang digunakan untuk menunjukkan diferensiasi, dan notasi kotak sulit untuk direproduksi oleh printer, jadi notasi tersebut tidak digunakan secara luas.
Penggunaan pertama dari istilah tersebut[sunting | sunting sumber]
Istilah ini pertama kali dicetak dalam bahasa Latin pada tahun 1690: "Ergo et horum Integralia aequantur" (Bernoulli, Opera 1744, Vol. 1, hal. 423).[8]
Istilah ini digunakan dalam paragraf yang mudah dipahami dari Guillaume de l'Hôpital pada tahun 1696:[9]
Dans tout cela il n'y a encore que la premiere partie du calcul de M. Leibniz, laquelle consiste à descendre des grandeurs entiéres à leur différences infiniment petites, et à comparer entr'eux ces infiniment petits de quelque genre qu'ils soient: c'est ce qu'on appel calcul différentiel. Pour l'autre partie, qu'on appelle Calcul intégral, et qui consiste à remonter de ces infiniment petits aux grandeurs ou aux touts dont ils sont les différences, c'est-à-dire à en trouver les sommes, j'avois aussi dessein de le donner. Mais M. Leibniz m'ayant écrit qu'il y travailloit dans un Traité qu'il intitule De Scientia infiniti, je n'ay eu garde de prive le public d'un si bel Ouvrage qui doit renfermer tout ce qu'il y a de plus curieux pour la Méthode inverse des Tangentes...
"Dalam semua itu, hanya ada bagian pertama dari kalkulus M. Leibniz, yang terdiri dari turun dari besaran integral ke perbedaan kecil tak terhingga, dan dalam membandingkan antara satu sama lain yang sangat kecil tak terhingga dari jenis yang mungkin: inilah yang disebut kalkulus diferensial. Adapun bagian lain, yang disebut kalkulus integral, dan itu terdiri dari kembali ke atas dari yang sangat kecil ke kuantitas, atau bagian penuh dari perbedaan mereka, yaitu untuk menemukan jumlah mereka, saya juga berniat untuk mengungkapkannya. Tetapi mengingat M. Leibniz menulis kepada saya bahwa dia sedang mengerjakannya di sebuah buku yang dia sebut De Scientia infiniti, Saya berhati-hati untuk tidak menghilangkan publik dari karya yang begitu indah yang karena mengandung semua yang paling aneh dalam metode kebalikan dari garis singgung..."
Interpretasi dari integral[sunting | sunting sumber]
Integral muncul dalam banyak situasi praktis. Bila sebuah kolam renang berbentuk persegi panjang dengan dasar datar, maka dari panjang, lebar, dan dalamnya kita dapat dengan mudah menentukan volume air yang dapat ditampungnya (untuk mengisinya), luas permukaannya (untuk menutupinya), dan panjang tepinya (untuk mengikatnya). Tetapi jika berbentuk oval dengan dasar bulat, semua besaran ini membutuhkan integral. Perkiraan praktis mungkin cukup untuk contoh sepele seperti itu, tetapi teknik presisi (dari disiplin apa pun) membutuhkan nilai yang tepat dan teliti untuk elemen ini.
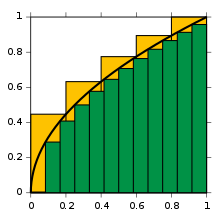
Untuk memulai, pertimbangkan kurva y = f(x) antara x = 0 dan x = 1 dengan f(x) = √x (lihat gambar). Kami bertanya:
- Berapakah luas di bawah fungsi f, dalam interval dari 0 sampai 1?
dan menyebut luas dari (belum diketahui) sebagai (pasti) integral dari f. Notasi untuk integral ini adalah
Sebagai perkiraan pertama, lihat persegi satuan yang diberikan oleh sisi-sisinya x = 0 ke x = 1 dan y = f(0) = 0 dan y = f(1) = 1. Luasnya persis 1. Sebenarnya, nilai sebenarnya dari integral harus kurang dari 1. Mengurangi lebar persegi panjang aproksimasi dan menambah jumlah persegi panjang memberikan hasil yang lebih baik; jadi silangkan interval dalam lima langkah, menggunakan titik aproksimasi 0, 1/5, 2/5, dan seterusnya ke 1. Pasangkan kotak untuk setiap langkah dengan menggunakan tinggi ujung kanan setiap bagian kurva, sehingga √1/5, √2/5, dan seterusnya √1 = 1. Dengan menjumlahkan luas persegi panjang ini, kita akan mendapatkan pendekatan yang lebih baik untuk integral yang dicari, yaitu
Kami mengambil jumlah nilai fungsi yang tak terhingga dari f, dikalikan dengan selisih dua titik aproksimasi berikutnya. Kita dapat dengan mudah melihat bahwa perkiraannya masih terlalu besar. Menggunakan lebih banyak langkah menghasilkan perkiraan yang lebih dekat, tetapi akan selalu terlalu tinggi dan tidak akan pernah tepat. Alternatifnya, mengganti sub-interval ini dengan satu dengan tinggi ujung kiri setiap bagian, kita akan mendapatkan perkiraan yang terlalu rendah: contohnya, dengan dua belas subinterval seperti itu, kita akan mendapatkan nilai perkiraan untuk luas 0,6203.
Ide kuncinya adalah transisi dari menambahkan perbedaan titik aproksimasi sangat banyak (dikalikan dengan nilai fungsinya masing-masing) menjadi menggunakan halus tak terhingga, atau infinitesimal. Ketika transisi ini diselesaikan pada contoh di atas, ternyata luas di bawah kurva dalam batas yang disebutkan adalah 2/3.
Notasi dari
menganggap integral sebagai jumlah tertimbang, dilambangkan dengan memanjang s, nilai fungsi, f(x), dikalikan dengan lebar langkah yang sangat kecil, yang disebut diferensial, dilambangkan dengan dx.
Secara historis, setelah kegagalan upaya awal untuk menafsirkan infinitesimal secara ketat, Riemann secara formal mendefinisikan integral sebagai limit dari jumlah tertimbang, sehingga dx menyarankan batas perbedaan (yaitu, lebar interval). Kekurangan ketergantungan Riemann pada interval dan kontinuitas memotivasi definisi yang lebih baru, terutama integral Lebesgue, yang didasarkan pada kemampuan untuk memperluas gagasan "mengukur" dengan cara yang jauh lebih fleksibel. Demikian notasinya
mengacu pada jumlah tertimbang di mana nilai fungsi dipartisi, dengan μ mengukur bobot yang akan diberikan untuk setiap nilai. Di sini A menunjukkan wilayah integral.
Definisi formal[sunting | sunting sumber]
Ada banyak cara untuk mendefinisikan integral secara formal, tidak semuanya setara. Perbedaan tersebut sebagian besar ada untuk menangani kasus khusus yang berbeda yang mungkin tidak dapat diintegrasikan dalam definisi lain, tetapi juga jarang terjadi karena alasan pedagogis. Definisi integral yang paling umum digunakan adalah integral Riemann dan integral Lebesgue.
Integral Riemann[sunting | sunting sumber]
Integral Riemann didefinisikan dalam istilah jumlah Riemann fungsi sehubungan dengan partisi yang ditandai dari sebuah interval.[10] Maka [a, b] salah satu bagian interval tertutup dari garis nyata; lalu "partisi yang diberi tag" dari [a, b] adalah urutan yang terbatas
Cara membagi interval pada [a, b] menjadi n mengganti dengan interval [xi−1, xi] diindeks oleh i, yang masing-masing "diberi tag" dengan titik yang berbeda ti ∈ [xi−1, xi]. A Jumlah Riemann dari suatu fungsi f sehubungan dengan partisi yang ditandai seperti definisi sebagai
dengan demikian setiap suku dari jumlah tersebut adalah luas persegi panjang dengan tinggi sama dengan nilai fungsi pada titik yang dibedakan dari sub-interval yang diberikan, dan lebarnya sama dengan lebar sub-interval. Maka Δi = xi−xi−1 menjadi lebar sub-interval i; maka menghubungkan partisi yang diberi tag adalah lebar mengganti interval terbesar yang dibentuk oleh partisi, maxi=1...n Δi. Integral Riemann dari sebuah fungsi f selama interval [a, b] sama dengan S jika:
- Untuk semua nilai ε > 0 disana terdapat jumlah δ > 0 sedemikian rupa, untuk partisi yang diberi tag [a, b] dengan mesh kurang dari δ, kami punya
Ketika tag yang dipilih memberikan nilai maksimum (masing-masing, minimum) dari setiap interval, jumlah Riemann menjadi atas (masing-masing, lebih rendah) Jumlah Darboux, menunjukkan hubungan erat antara integral Riemann dan integral Darboux.
Integral Lebesgue[sunting | sunting sumber]
Seringkali menarik, baik dalam teori maupun aplikasi, untuk dapat melewati batas di bawah integral. Contohnya, urutan fungsi sering kali dapat dibangun yang mendekati, dalam arti yang sesuai, solusi untuk suatu masalah. Jadi integral dari fungsi solusi harus menjadi batas integral dari aproksimasi. Akan tetapi, banyak fungsi yang dapat diperoleh sebagai batas bukan merupakan integral Riemann, sehingga teorema batas tersebut tidak berlaku dengan integral Riemann.. Oleh karena itu, sangat penting untuk memiliki definisi integral yang memungkinkan kelas fungsi yang lebih luas untuk diintegralkan (Rudin 1987).
Integral seperti itu adalah integral Lebesgue, yang mengeksploitasi fakta berikut untuk memperbesar kelas fungsi yang dapat diintegrasikan: Bila nilai suatu fungsi disusun ulang di atas domain, integral dari suatu fungsi harus tetap sama. Jadi Henri Lebesgue memperkenalkan integral yang menyandang namanya, menjelaskan integral ini dalam sebuah surat kepada Paul Montel:
Saya harus membayar sejumlah uang, yang telah saya kumpulkan di saku saya. Saya mengambil uang kertas dan koin dari saku saya dan memberikannya kepada kreditor sesuai urutan saya menemukannya sampai saya mencapai jumlah totalnya. Ini adalah integral Riemann. Tetapi saya dapat melanjutkan secara berbeda. Setelah saya mengeluarkan semua uang dari saku saya Saya memesan uang kertas dan koin sesuai dengan nilai yang sama dan kemudian saya membayar beberapa tumpukan satu demi satu kepada kreditor. Ini adalah bagian integral saya.
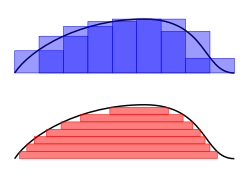
Sebagai (Folland 1984, p. 56) meletakkannya, "Untuk menghitung integral Riemann dari f, satu partisi domain [a, b] menjadi sub-interval ", sementara dalam integral Lebesgue," salah satunya adalah mempartisi kisaran f ". Definisi integral Lebesgue dengan demikian dimulai dengan ukuran, μ. Dalam kasus yang paling sederhana, ukuran Lebesgue μ(A) dari sebuah interval A = [a, b] adalah lebar, b − a, sehingga integral Lebesgue setuju dengan integral Riemann (yang tepat) ketika keduanya ada. Dalam kasus yang lebih rumit, set yang diukur bisa sangat terfragmentasi, tanpa kontinuitas dan tidak ada kemiripan dengan interval.
Menggunakan "partisi rentang f " filsafat, integral dari fungsi non-negatif f : R → R harus berjumlah lebih dari t dari area di antara strip horizontal tipis di antaranya y = t and y = t + dt. Maka hasil dari daerah μ{ x : f(x) > t} dt. Maka f∗(t) = μ{ x : f(x) > t}. Integral Lebesgue dari f kemudian didefinisikan oleh (Lieb & Loss 2001)
dimana integral di sebelah kanan adalah integral Riemann biasa yang tidak layak (f∗ is a menurunkan fungsi positif secara ketat, dan karena itu memiliki terdefinisi dengan baik integral Riemann yang tidak tepat). Untuk kelas fungsi yang sesuai (fungsi terukur s) ini mendefinisikan integral Lebesgue.
Fungsi umum yang dapat diukur f adalah Integrasi Lebesgue jika jumlah nilai absolut dari luas daerah antara grafik f dan sumbu x terbatas:
Dalam kasus tersebut, integralnya adalah, seperti dalam kasus Riemannian, perbedaan antara luas di atas sumbu x dan luas di bawah sumbu x:
dimana
Integral Darboux[sunting | sunting sumber]
Integral Darboux, yang ditentukan oleh jumlah Darboux (jumlah Riemann terbatas) namun ekuivalen dengan integral Riemann suatu fungsi dapat diintegrasikan dengan Darboux jika dan hanya jika ia dapat diintegrasikan dengan Riemann. Integral Darboux memiliki keuntungan karena lebih mudah didefinisikan daripada integral Riemann.
Partisi interval [a,b] adalah urutan nilai yang terbatas xi seperti yang
Setiap interval [xi−1,xi] disebut subinterval dari partisi. Membiarkan ƒ:[a,b]→ℝ menjadi fungsi yang dibatasi, dan jika
menjadi partisi dari [a, b]. Maka

Jumlah Darboux atas dari ƒ sehubungan dengan P adalah
Jumlah Darboux bawah dari ƒ sehubungan dengan P adalah
Jumlah Darboux bawah dan atas sering disebut jumlah bawah dan atas.
Integral Riemann–Stieltjes[sunting | sunting sumber]
Integral Riemann-Stieltjes, perpanjangan dari integral Riemann yang terintegrasi sehubungan dengan fungsi sebagai lawan dari variabel.
Riemann-Stieltjes integral dari fungsi bernilai nyata variabel nyata pada interval sehubungan dengan fungsi real-to-real lainnya dilambangkan dengan
menggunakan urutan partisi dari interval
Integral, kemudian, didefinisikan sebagai limit, karena norma (panjang dari subinterval terpanjang) dari partisi mendekati , dari jumlah perkiraan
Integral Lebesgue–Stieltjes[sunting | sunting sumber]
Integral Lebesgue–Stieltjes, dikembangkan lebih lanjut oleh Johann Radon, yang menggeneralisasi integral Riemann–Stieltjes dan Lebesgue.
Integral lainnya[sunting | sunting sumber]
Integral lainnya yang terdapat di bawah ini:
- Integral Daniell, yang mengasumsikan integral Lebesgue dan integral Lebesgue–Stieltjes tanpa bergantung pada pengukuran.
- Integral Haar, digunakan untuk integrasi pada kelompok topologi kompak secara lokal, diperkenalkan oleh Alfréd Haar pada tahun 1933.
- Integral Henstock–Kurzweil, dengan berbagai variasi didefinisikan oleh Arnaud Denjoy, Oskar Perron, dan (paling elegan, sebagai integral pengukur) Jaroslav Kurzweil, dan dikembangkan oleh Ralph Henstock.
- Integral Itô dan Integral Stratonovich, yang mendefinisikan integral sehubungan dengan semi persegi panjang seperti gerak Brown.
- Integral Young, yang merupakan sejenis integral Riemann-Stieltjes sehubungan dengan fungsi tertentu dari variasi tak terbatas.
- Integral jalur kasar, yang ditentukan untuk fungsi yang dilengkapi dengan beberapa "jalur kasar" tambahan menyusun dan menggeneralisasi integrasi stokastik terhadap semi persegi panjang dan proses seperti gerakan pecahan Brownian.
- Integral Choquet, integral subaditif atau superaditif yang dibuat oleh ahli matematika Prancis Gustave Choquet pada tahun 1953.
Sifat[sunting | sunting sumber]
Linearitas[sunting | sunting sumber]
Kumpulan fungsi yang dapat diintegrasikan Riemann pada interval tertutup [a, b] membentuk ruang vektor di bawah operasi penambahan pointwise dan perkalian dengan skalar, dan operasi integral
adalah fungsional linear pada ruang vektor ini. Jadi, pertama, kumpulan dari fungsi terintegral ditutup pada pengambilan kombinasi linier; dan kedua, integral dari kombinasi linier adalah kombinasi linier dari integral,[3]
Demikian pula, himpunan nyata - nilai fungsi terintegralkan Lebesgue pada ruang ukur yang diberikan E dengan ukuran μ ditutup dengan mengambil kombinasi linier, dan karenanya membentuk ruang vektor, dan integral Lebesgue
adalah fungsi linear pada ruang vektor ini, sehingga
Secara lebih umum, pertimbangkan ruang vektor dari semua fungsi terukur pada ruang ukur (E,μ), mengambil nilai dalam kompak lokal lengkap spasi vektor topologi V di atas bidang topologi K, f : E → V. Kemudian seseorang dapat mendefinisikan peta integrasi abstrak yang ditugaskan ke setiap fungsi f sebuah elemen dari V atau simbol ∞,
kompatibel dengan kombinasi linear. Dalam situasi ini, linieritas berlaku untuk subruang fungsi yang integralnya merupakan elemen dari V (yaitu "finite"). Kasus khusus yang paling penting muncul adalah K pada R, C, atau perluasan lapangan yang terbatas Qp dari bilangan p-adic s, dan V adalah ruang vektor berdimensi-hingga di atas K, dan jika K = C dan V adalah kompleks ruang Hilbert.
Linearitas, bersama dengan beberapa sifat kontinuitas alami dan normalisasi untuk kelas fungsi "sederhana" tertentu, dapat digunakan untuk memberikan definisi alternatif dari integral. Ini adalah pendekatan dari Daniell untuk kasus fungsi bernilai riil pada suatu himpunan X, digeneralisasikan oleh Nicolas Bourbaki ke fungsi dengan nilai dalam ruang vektor topologi yang kompak secara lokal. Lihat (Hildebrandt 1953) untuk karakterisasi aksiomatik dari integral.
Lihat pula[sunting | sunting sumber]
Referensi[sunting | sunting sumber]
- ^ a b c Kesalahan pengutipan: Tag
<ref>tidak sah; tidak ditemukan teks untuk ref bernama:0 - ^ a b Kesalahan pengutipan: Tag
<ref>tidak sah; tidak ditemukan teks untuk ref bernama:1 - ^ a b Kesalahan pengutipan: Tag
<ref>tidak sah; tidak ditemukan teks untuk ref bernama:2 - ^ Pada abad ke-20, analisis non-standar dikembangkan sebagai pendekatan baru untuk kalkulus yang menggabungkan konsep ketat infinitesimals dengan menggunakan sistem bilangan yang diperluas yang disebut bilangan hiperriil. Meskipun ditempatkan pada pijakan aksiomatik yang sehat dan kepentingan dalam dirinya sendiri sebagai area investigasi baru, analisis nonstandar tetap agak kontroversial dari sudut pandang pedagogis, dengan pendukung menunjukkan sifat intuitif infinitesimals untuk siswa pemula kalkulus dan penentang mengkritik kompleksitas logis dari sistem secara keseluruhan.
- ^ (W3C 2006).
- ^ Heath, Thomas Little (1897). Karya Archimedes. Inggris: Cambridge University Publications.
- ^ Katz, V.J. 1995. "Ide Kalkulus dalam Islam dan India." Majalah Matematika (Asosiasi Matematika Amerika), 68(3):163–174.
- ^ Roero, C.S. (2005), "Gottfried Wilhelm Leibniz, tiga makalah pertama tentang kalkulus (1684, 1686, 1693)", Landmark Writings in Western Mathematics 1640-1940 (dalam bahasa Inggris), Elsevier, hlm. 46–58, doi:10.1016/b978-044450871-3/50085-1, ISBN 978-0-444-50871-3
- ^ L'Hospital, Guillaume-François-Antoine de (1661-1704) Auteur du texte (1696). Analyse des infiniment petits, pour l'intelligence des lignes courbes (dalam bahasa Bahasa Inggris).
- ^ (Inggris) Weisstein, Eric W. "Riemann Sum". MathWorld.
Bacaan lebih lanjut[sunting | sunting sumber]
- Kurnianingsih, Sri (2007). Matematika SMA dan MA 3A Untuk Kelas XII Semester 1 Program IPA. Jakarta: Esis/Erlangga. ISBN 979-734-504-1. (Indonesia)
- Kurnianingsih, Sri (2007). Matematika SMA dan MA 3A Untuk Kelas XII Semester 1 Program IPS. Jakarta: Esis/Erlangga. ISBN 979-734-567-X. (Indonesia)
Pranala luar[sunting | sunting sumber]
- (Indonesia) Operator Integrasi Berulang[pranala nonaktif permanen]


























![{\displaystyle {\begin{aligned}M_{i}=\sup _{x\in [x_{i-1},x_{i}]}f(x),\\m_{i}=\inf _{x\in [x_{i-1},x_{i}]}f(x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c17d20124547d96a57c5e6cd4386d88abaa622a4)



![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)





![{\displaystyle S(P,f,g)=\sum _{i=0}^{n-1}f(c_{i})\left[g(x_{i+1})-g(x_{i})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b60856e31ea522340fba3119751286c72478a02d)




