Teorema Taylor
| Kalkulus |
|---|
Dalam kalkulus, teorema Taylor menyatakan bahwa suatu fungsi yang terdiferensiasi dapat dinyatakan dalam suatu deret pangkat atau suku banyak (polinomial). Koefisien polinomial tersebut hanya tergantung pada turunan fungsi pada titik yang bersangkutan. Lebih lanjut, teorema ini juga memberikan estimasi nilai galat dari seberapa banyaknya barisan dalam deret yang digunakan. Teorema ini mendapat nama dari matematikawan Brook Taylor, yang menyatakannya pada tahun 1712, meskipun hasilnya sudah ditemukan pertama kali tahun 1671 oleh James Gregory.
Teorema Taylor dalam satu variabel
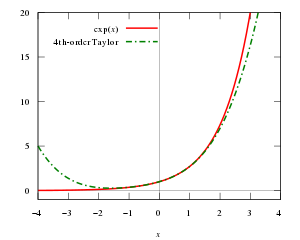
[sunting | sunting sumber]Teorema Taylor menyatakan setiap fungsi mulus dapat dihampiri dengan polinomial. Contoh sederhana penerapan teorema Taylor adalah hampiran fungsi eksponensial ex di dekat x = 0:
Hampiran ini dinamakan hampiran Taylor orde ke-n' terhadap ex karena menghampiri nilai fungsi eksponensial menggunakan polinomial derajat n. Hampiran ini hanya berlaku untuk x mendekati nol, dan bila x bergerak menjauhi nol, hampiran ini menjadi semakin buruk. Kualitas hampiran dinyatakan oleh suku sisa:
Lebih umum lagi, teorema Taylor berlaku untuk setiap fungsi yang dapat diturunkan ƒ, dengan hampiran untuk x di dekat titik a, dalam bentuk:
Suku sisa adalah perbedaan antara fungsi dan polinomial hampirannya:
Meskipun rumus eksplisit untuk suku sisa ini jarang digunakan, teorema Taylor juga memberikan estimasi nilai sisanya. Dengan kata lain, untuk x cukup dekat terhadap a, suku sisa haruslah cukup kecil. Teorema Taylor memberikan informasi persis seberapa kecil suku sisa tersebut.
Pernyataan
[sunting | sunting sumber]Pernyataan cermat teorema ini adalah sebagai berikut: bila n ≥ 0 adalah bilangan bulat dan f adalah fungsi yang terturunkan kontinu pada selang tertutup [a, x] dan terturunkan n + 1 kali pada selang terbuka (a, x), maka
Di sini n! melambangkan n faktorial dan Rn(x) adalah suku sisa, melambangkan beda antara polinomial Taylor derajat-n terhadap fungsi asli. Suku sisa Rn(x) tergantung pada x, dan kecil bila x cukup dekat terhadap a. Ada beberapa pernyataan untuk suku sisa ini.
Bentuk Lagrange[1] dari suku sisa menyatakan bahwa terdapat bilangan ξ antara a dan x sedemikian sehingga
Ini mengungkapkan teorema Taylor sebagai perampatan teorema nilai rata-rata. Sebenarnya, teorema nilai rata-rata digunakan untuk membuktikan teorema Taylor dengan suku sisa bentuk Lagrange.
Bentuk Cauchy[2] suku sisa menyatakan bahwa terdapat bilangan ξ antara a dan x sehingga
Secara umum, bila G(t) adalah fungsi kontinu pada selang tertutup [a,x], yang terturunkan dengan turunan tidak nol pada (a,x), maka ada suatu bilangan ξ antara a dan x sehingga
Ini mengungkapkan teorema Taylor sebagai generalisasi teorema nilai rata-rata Cauchy.
Bentuk di atas terbatas pada fungsi riil. Namun bentuk integral[3] dari suku sisa juga berlaku untuk fungsi kompleks, yaitu:
dengan syarat, seperti yang biasa ditemui, fn kontinu mutlak dalam [a, x]. Ini menunjukkan teorema ini sebagai perampatan teorema dasar kalkulus.
Secara umum, suatu fungsi tidak perlu sama dengan deret Taylor-nya, karena mungkin saja deret Taylor tersebut tidak konvergen, atau konvergen menuju fungsi yang berbeda. Namun, untuk banyak fungsi f(x), kita dapat menunjukkan bahwa suku sisa Rn mendekati nol saat n mendekati ∞. Fungsi-fungsi tersebut dapat dinyatakan sebagai deret Taylor pada persekitaran titik a, dan disebut sebagai fungsi analitik.
Estimasi suku sisa
[sunting | sunting sumber]Versi umum teorema Taylor lainnya berlaku pada selang (a − r, a + r) tempat variabel x mengambil nilainya. Perumusan teorema ini memiliki keuntungan bahwa mungkin mengendalikan ukuran suku-suku sisa, dan dengan demikian kita dapat menghitung hampiran fungsi yang sahih pada seluruh selang, dengan batas yang cermat untuk mutu hampirannya.
Versi yang cermat untuk teorema Taylor dalam bentuk ini adalah sebagai berikut. Misalkan ƒ adalah fungsi yang terturunkan kontinu n kali pada selang tertutup [a - r, a + r] dan terturunkan n + 1 kali pada selang terbuka (a − r, a + r). Bila ada konstanta positif riil Mn sedemikian sehingga |ƒ(n+1)(x)| ≤ Mn untuk semua x ∈ (a − r, a + r), maka
di mana fungsi sisa Rn memenuhi ketidaksamaan (dikenal sebagai estimasi Cauchy)
untuk semua x ∈ (a − r, a + r). Ini disebut sebagai estimasi seragam galat pada polinomial Taylor yang terpusat pada a, karena ini berlaku seragam untuk setiap x dalam selang.
Bila ƒ adalah fungsi mulus pada [a − r, a + r], maka konstanta positif Mn ada untuk tiap n = 1, 2, 3, … sedemikian sehingga | ƒ(n+1)(x)| ≤ Mn untuk semua x ∈ (a − r, a + r). Tambahan lagi, jika mungkin memilih konstanta ini, sehingga
- as
maka ƒ adalah fungsi analitik pada (a − r, a + r). Secara khusus, suku sisa pada hampiran Taylor, Rn(x) cenderung menuju nol secara seragam saat n→∞. Dengan kata lain, fungsi analitik adalah limit seragam dari polinomial Taylornya pada sebuah selang.
Pembuktian: satu variabel
[sunting | sunting sumber]Berikut adalah bukti teorema Taylor dengan suku sisa integral[4]
Teorema dasar kalkulus menyatakan bahwa
yang dapat disusun ulang menjadi:
Sekarang kita dapat melihat bahwa penerapan integrasi parsial menghasilkan
Persamaan pertama diperoleh dengan memisalkan dandv = dt; persamaan kedua didapatkan dengan mencatat bahwa ; yang ketiga didapatkan dengan mengeluarkan faktor yang sama.
Bila integrasi parsial ini diteruskan didapatkan:
Dengan mengulangi proses ini, kita dapat menurunkan teorema Taylor untuk nilai n yang lebih tinggi.
Proses ini dapat diformalkan dengan menerapkan teknik induksi matematika. Jadi misalkan teorema Taylor berlaku unutk n tertentu, yaitu, misalkan
Kita dapat menulis ulang integral dengan integrasi parsial. Sebuah antiturunan (x − t)n sebagai fungsi dari t diberikan sebagai −(x−t)n+1 / (n + 1), sehingga
Mensubstitusikan ini dalam (*) membuktikan teorema Taylor untuk n + 1, dan karenanya untuk semua n bilangan bulat non-negatif.
Suku sisa dalam bentuk Lagrange dapat diturunkan dengan teorema nilai rata-rata untuk integral dengan cara berikut:
di mana ξ adalah suatu bilangan dari selang [a, x]. Integral terakhir dapat dievaluasi langsung, yang menghasilkan
Secara lebih umum, untuk tiap fungsi G(t), teorema nilai rata-rata menjamin eksistensi ξ dalam selang [a,x] yang memenuhi
Teorema Taylor dalam satu variabel nyata
[sunting | sunting sumber]Pernyataan teorema
[sunting | sunting sumber]Pernyataan dari versi paling dasar dari teorema Taylor adalah sebagai berikut:
Teorema Taylor.[5][6][7] Let k ≥ 1 jika nilai pada integer dan biarkan nilai fungsi f : R → R jika nilai k kali ini dapat dibedakan pada titik tersebut a ∈ R. Setelah itu fungsi pada hk : R → R, dirumuskan:
. Hal ini disebut juga Peano.
Hasil teorema yang muncul dalam teorema Taylor adalah k urutan pada Teorema Taylor, yaitu:
dari fungsi f pada titik a. Teorema Taylor adalah Teorema yang digunakan dalam arti, jika terdapat suatu fungsi hk : R → R dan k ke order teorema ``p dengan sedemikian rupa
setelah itu p = Pk. Teorema Taylor menggambarkan perilaku asimtotik dari istilah sisa
Salah satu kesalahan aproksimasi saat mendekati nilai f dengan teorema taylor. Menggunakan notasi o kecil, pernyataan dalam teorema Taylor dibaca sebagai berikut
Rumus eksplisit untuk sisa
[sunting | sunting sumber]Di bawah asumsi keteraturan yang lebih kuat pada nilai f ada beberapa rumus yang tepat untuk istilah sisa pada Rk dari teorema taylor, yang paling relevan adalah sebagai berikut.
Bentuk nilai rata-rata dari sisa. Mari mencari nilai f : R → R berada pada nilai k + 1 saat kita dapat membedakan pada interval terbuka dengan f(k) saat fungsi kontinu pada interval tertutup antara a serta x.[8] Kemudian
untuk beberapa bilangan real pada nilai ξL di antara nilai a dan x. Hal tersebut adalah dari Lagrange[9] pada sisa pernyataan.
Demikian pula,
untuk beberapa bilangan real pada ξC di antara a dan x. Hal tersebut adalah bentuk dari Cauchy[10] dari sisa pernyataan.
Perbaikan teorema Taylor tersebut terbiasa dibuktikan menggunakan teorema nilai rata-rata, dari mana namanya. Hal tersebut ekspresi serupa lainnya. Contoh dari G(t) kontinu pada interval tertutup dan dapat dibedakan dengan turunan pada interval terbuka di antaranya a dan x, maka
Untuk beberapa nomor ξ di antara a dan x. Versi tersebut mencakup bentuk Lagrange dan Cauchy sisanya sebagai kasus khusus dan dibuktikan dengan penggunaan di bawah Teorema Nilai Rata-rata Cauchy.
Pernyataan dalam bentuk integral dari sisa lebih maju dari yang sebelumnya, dan membutuhkan pemahaman tentang teori integrasi Lebesgue untuk pencarian penuh. Namun, itu berlaku juga dalam arti integral Riemann asalkan nilai (k + 1) keturunan dari f kontinu pada interval tertutup [a,x].
Bentuk integral dari sisanya.[11] Mari f(k) cara menjadikan bilangan berkelanjutan pada interval tertutup antara a dan x. Setelah itu
Estimasi untuk sisanya
[sunting | sunting sumber]Contoh
[sunting | sunting sumber]Catatan kaki
[sunting | sunting sumber]- ^ Klein (1998) 20.3; Apostol (1967) 7.7.
- ^ Apostol (1967) 7.7.
- ^ Apostol (1967) 7.5.
- ^ Perhatikan bahwa bukti ini mensyaratkan bahwa fn kontinu mutlak pada[a, x] sehingga teorema dasar kalkulus berlaku. Kecuali pada bagian akhir saat teorema nilai rata-rata diterapkan, keterdiferensialan fn tidak perlu diasumsikan, karena kekontinan mutlak menyiratkan keterdiferensialan hampir di mana saja, serta kesahihan teorema dasar kalkulus, dengan syarat integral yang terlibat dipahami sebagai integral Lebesgue. Sebagai akibatnya, bentuk integral suku sisa berlaku dengan pelemahan asumsi terhadap f.
- ^
 Catatan:
Catatan:
- ^ Spivak, Michael (1994), Calculus (edisi ke-3rd), Houston, TX: Publish or Perish, hlm. 383, ISBN 978-0-914098-89-8
- ^ Hazewinkel, Michiel, ed. (2001) [1994], "Taylor formula", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
- ^
- ^ Kline 1998, §20.3; Apostol 1967, §7.7.
- ^ Apostol 1967, §7.7.
- ^ Apostol 1967, §7.5.
Rujukan
[sunting | sunting sumber]- Apostol, Tom (1967). Calculus. Jon Wiley & Sons, Inc. ISBN 0-471-00005-1.
- Klein, Morris (1998). Calculus: An Intuitive and Physical Approach. Dover. ISBN 0-486-40453-6.
Pranala luar
[sunting | sunting sumber]- (Inggris)Trigonometric Taylor Expansion Applet demonstrasi interaktif
- (Inggris)Taylor Series Revisited Diarsipkan 2008-10-10 di Wayback Machine. pada Holistic Numerical Methods Institute























![{\displaystyle {}=-\left[{\frac {f^{(n+1)}(t)}{(n+1)n!}}(x-t)^{n+1}\right]_{a}^{x}+\int _{a}^{x}{\frac {f^{(n+2)}(t)}{(n+1)n!}}(x-t)^{n+1}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc99323e086d38a067e9710a7a90f863384694b)














