Geometri aljabar
Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. (January 2020) |

| Geometri |
|---|
 |
| Ahli geometri |
Geometri aljabar merupakan cabang matematika yang mempelajari akar dari suatu suku banyak. Dalam kajian modern, digunakan berbagai alat dari aljabar abstrak seperti aljabar komutatif dan teori kategori. Studi geometri aljabar dilakukan dengan mengonstruksi suatu objek matematika (misalnya, skema dan sheaf) lalu kemudian meninjau hubungannya dengan struktur yang sudah dikenal. Berbagai alat ini dibuat untuk membantu memahami permasalahan mendasar terkait geometri.[1]
Salah satu objek fundamental dalam studi geometri aljabar adalah varietas aljabarik yang merupakan manifestasi geometris dari akar suatu sistem suku banyak. Dari struktur ini, dapat dikaji berbagai kurva aljabarik seperti garis, parabola, elips, kurva eliptik dan lain-lain.
Geometri aljabar merupakan salah satu topik sentral dalam matematika dengan berbagai topik terkait seperti analisis kompleks, topologi, teori bilangan, teori kategori, dan lain-lain.
Geometri aljabar menempati tempat sentral dalam matematika modern dan memiliki beberapa hubungan konseptual dengan berbagai bidang seperti analisis kompleks, topologi dan teori bilangan. Awalnya studi tentang sistem persamaan polinomial dalam beberapa variabel, subjek geometri aljabar dimulai di mana pemecahan persamaan berhenti, ini mengarah ke beberapa daerah terdalam dalam semua matematika, baik secara konseptual maupun dalam istilah teknik.
Pada abad ke-20, geometri aljabar terpecah menjadi beberapa subdaerah.
- Arus utama geometri aljabar dikhususkan untuk mempelajari titik-titik kompleks dari varietas aljabar dan lebih umum lagi pada titik-titik dengan koordinat dalam bidang tertutup aljabar.
- Geometri aljabar real adalah ilmu yang mempelajari titik-titik real dari suatu ragam aljabar.
- Geometri Diofantin dan, secara lebih umum, geometri aritmetika adalah studi tentang titik varietas aljabar dengan koordinat di bidang yang tidak tertutup secara aljabar dan terjadi di teori bilangan aljabar, seperti bidang bilangan rasional, bidang bilangan, bidang terbatas, bidang fungsi, dan bilangan p-adik.
- Sebagian besar teori singularitas dikhususkan untuk singularitas varietas aljabar.
- Geometri aljabar komputasi adalah area yang muncul di persimpangan geometri aljabar dan aljabar komputer, dengan munculnya komputer. Ini terutama terdiri dari algoritme desain dan perangkat lunak pengembangan untuk mempelajari sifat dari varietas aljabar yang diberikan secara eksplisit.
Banyak perkembangan arus utama geometri aljabar di abad ke-20 terjadi dalam kerangka aljabar abstrak, dengan peningkatan penekanan ditempatkan pada sifat "intrinsik" dari varietas aljabar yang tidak bergantung pada cara tertentu untuk menanamkan varietas dalam ruang koordinat ambien; ini paralel dengan perkembangan dalam topologi, diferensial dan geometri kompleks. Salah satu pencapaian utama geometri aljabar abstrak ini adalah Grothendieck pada teori skema yang memungkinkan salah satunya untuk menggunakan teori gemal untuk mempelajari varietas aljabar dengan cara yang sangat mirip dengan penggunaannya dalam studi lipatan diferensial dan analitik. Ini diperoleh dengan memperluas pengertian titik: Dalam geometri aljabar klasik, titik dari varietas afin dapat diidentifikasi, melalui Hilbert Nullstellensatz, dengan ideal maksimal dari gelanggang koordinat, sedangkan titik dari skema afin yang sesuai adalah semua ideal utama dari gelanggang ini. Ini berarti bahwa titik dari skema seperti itu dapat berupa titik biasa atau subvarietas. Pendekatan ini juga memungkinkan penyatuan bahasa dan alat geometri aljabar klasik, terutama berkaitan dengan titik kompleks, dan teori bilangan aljabar. Bukti Wiles dari konjektur lema yang disebut Teorema terakhir Fermat adalah contoh kekuatan pendekatan ini.
Pengertian dasar[sunting | sunting sumber]
Angka nol dari polinomial simultan[sunting | sunting sumber]
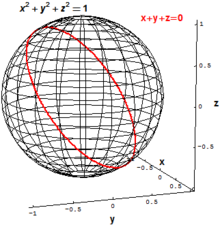
Dalam geometri aljabar klasik, objek utama yang menarik adalah kumpulan kumpulan polinomial yang hilang, artinya himpunan semua titik yang secara bersamaan memenuhi satu atau lebih persamaan polinomial. Misalnya, dua dimensi pada bola dengan jari-jari 1 dalam tiga dimensi dalam Ruang Euklides dapat didefinisikan sebagai himpunan semua titik dengan
Lingkaran "miring" pafd dapat didefinisikan sebagai himpunan semua titik yang memenuhi dua persamaan polinomial
Varietas afin[sunting | sunting sumber]
Pertama kita mulai dengan bidang . Dalam geometri aljabar klasik, bidang ini selalu berupa bilangan kompleks , tetapi banyak dari hasil yang sama benar jika kita mengasumsikan bahwa saja tertutup secara aljabar. Kita menganggap ruang afin dari dimensi atas , dilambangkan (atau lebih sederhananya , ketika jelas dari konteksnya). Ketika salah satunya menetapkan sistem koordinat, salah satunya dapat mengidentifikasi dengan . Tujuan tidak bekerja dengan adalah untuk menekankan bahwa salah satunya "melakukan" sesuatu dengan struktur ruang vektor pada .
Fungsi dikatakan sebagai polinomial (atau regular) jika dapat ditulis dengan polinomial, yaitu jika pada polinomial maka merupakan untuk titik dengan koordinat di . Sifat suatu fungsi menjadi polinomial (atau beraturan) tidak bergantung pada pilihan sistem koordinat di .
Ketika sistem koordinat dipilih, fungsi beraturan pada sebagai ruang afin dapat diidentifikasi dengan gelanggang fungsi polinomial dalam variabel pada . Oleh karena itu, himpunan fungsi beraturan pada adalah sebuah gelanggang yang dilambangkan .
Kita mengatakan bahwa polinomial lenyap pada suatu titik jika mengevaluasinya pada titik tersebut menghasilkan nol. Misalkan adalah kumpulan polinomial masuk . Himpunan lenyap dari atau himpunan nol adalah himpunan dari semua titik di An di mana setiap polinomial pada . Secara simbolis,
Bagian dari yang mana adalah , untuk suatu , disebut himpunan aljabar. adalah singkatan dari varietas (jenis himpunan aljabar tertentu akan didefinisikan di bawah).
Jawaban untuk pertanyaan pertama disediakan dengan memperkenalkan topologi Zariski, sebuah topologi aktif yang himpunan tertutupnya adalah himpunan aljabar, dan yang secara langsung mencerminkan struktur aljabar . Kemudian adalah bagian himpunan aljabar atau ekuivalen dengan himpunan tertutup Zariski. Jawaban untuk pertanyaan kedua diberikan oleh Hilbert's Nullstellensatz. Dalam salah satu bentuknya, dikatakan demikian adalah radikal dari ideal yang dihasilkan oleh . Dalam bahasa yang lebih abstrak, ada koneksi Galois, yang memunculkan dua operator penutupan; mereka dapat diidentifikasi, dan secara alami memainkan peran dasar dalam teori; contoh diuraikan pada koneksi Galois.
Untuk berbagai alasan kita mungkin tidak selalu ingin bekerja dengan seluruh ideal yang sesuai dengan himpunan aljabar . Teorema dasar Hilbert menyiratkan bahwa ideal dalam selalu terbangkit hingga.
Beberapa penulis tidak membuat perbedaan yang jelas antara himpunan aljabar dan varietas dan menggunakan varietas taktereduksi untuk membuat perbedaan bila diperlukan.
Fungsi beraturan[sunting | sunting sumber]
Sama seperti fungsi kontinu adalah peta alami pada ruang topologi dan fungsi mulus adalah peta alami pada manifold diferensial, terdapat kelas fungsi alami pada himpunan aljabar, yang disebut fungsi beraturan atau fungsi polinomial . fungsi beraturan pada himpunan aljabar yang terdapat di adalah batasan untuk dari fungsi beraturan di . Untuk himpunan aljabar yang ditentukan pada bidang bilangan kompleks, fungsi beraturannya adalah mulus dan genap analitik.
Mungkin tampak membatasi secara tidak wajar untuk mensyaratkan bahwa fungsi beraturan selalu diperluas ke ruang sekitar, tetapi sangat mirip dengan situasi pada normal ruang topologi, dimana Teorema keberadaan Tietze menjamin bahwa fungsi kontinu pada himpunan bagian tertutup selalu meluas ke ruang topologi sekitar.
Seperti halnya fungsi beraturan pada ruang afin, fungsi beraturan pada membentuk sebuah gelanggang, yang kita nyatakan dengan . Gelanggang ini disebut koordinat gelanggang dari .
Geometri aljabar real[sunting | sunting sumber]
Geometri aljabar real adalah ilmu yang mempelajari titik-titik real dari varietas aljabar.
Fakta bahwa bidang bilangan real adalah bidang terurut tidak dapat diabaikan dalam studi semacam itu. Misalnya, kurva persamaan adalah lingkaran jika , tetapi tidak memiliki titik real jika . Oleh karena itu, geometri aljabar real tidak hanya mempelajari varietas aljabar real, tetapi telah digeneralisasikan untuk mempelajari himpunan semi-aljabar, yang merupakan penyelesaian dari sistem persamaan polinomial dan pertidaksamaan polinomial. Misalnya, cabang dari persamaan hiperbola bukan ragam aljabar, tetapi himpunan semi-aljabar yang didefinisikan oleh dan atau oleh dan .
Salah satu masalah yang menantang dari geometri aljabar real adalah masalah keenam belas Hilbert yang takterpecahkan: Tentukan posisi masing-masing yang mungkin untuk oval dari kurva bidang taksingular.
Geometri aljabar komputasi[sunting | sunting sumber]
Bagian ini kosong. Anda bisa membantu dengan melengkapinya. |
Basis Gröbner[sunting | sunting sumber]
Bagian ini kosong. Anda bisa membantu dengan melengkapinya. |
Kompleksitas asimtotik vs. efisiensi praktis[sunting | sunting sumber]
Algoritme umum dasar dari geometri komputasi memiliki kasus terburuk eksponensial ganda kompleksitas. Lebih tepatnya, jika adalah derajat maksimal dari polinomial masukan dan jumlah variabel, kompleksitasnya paling banyak. untuk beberapa konstanta , dan, untuk beberapa masukan, paling tidak kompleksitasnya untuk konstanta lainnya.
Selama 20 tahun terakhir abad ke-20, berbagai algoritme telah diperkenalkan untuk menyelesaikan sub-masalah tertentu dengan kompleksitas yang lebih baik. Sebagian besar algoritme ini memiliki kompleksitas .[butuh rujukan]
Di antara algoritme ini yang memecahkan submasalah dari masalah yang dipecahkan oleh basis Gröbner, salah satunya dapat mengutip pengujian jika varietas afin kosong dan menyelesaikan sistem polinomial takhomogen. Algoritme semacam itu jarang diterapkan karena, pada sebagian besar entri Algoritme F4 dan F5 Faugère memiliki efisiensi praktis yang lebih baik dan mungkin kompleksitas yang serupa atau lebih baik (mungkin karena evaluasi kompleksitas algoritma dasar Gröbner pada kelas entri tertentu adalah tugas yang sulit yang telah dilakukan hanya dalam beberapa kasus khusus).
Algoritme utama geometri aljabar real yang memecahkan masalah yang diselesaikan dengan CAD berhubungan dengan topologi himpunan semi-aljabar. Salah satunya mungkin mengutip menghitung jumlah komponen yang terhubung, menguji jika dua titik berada dalam komponen yang sama atau menghitung stratifikasi Whitney dari himpunan aljabar real . Mereka memiliki kompleksitas , tetapi konstanta yang terlibat oleh notasi begitu tinggi sehingga menggunakannya untuk memecahkan masalah taktrivial yang secara efektif diselesaikan oleh CAD, tidak mungkin bahkan jika salah satunya dapat menggunakan semua daya komputasi yang ada. Oleh karena itu, algoritme ini belum pernah diimplementasikan dan ini merupakan area penelitian aktif untuk mencari algoritme yang memiliki kompleksitas asimtotik yang baik dan efisiensi praktis yang baik.
Lihat pula[sunting | sunting sumber]
Catatan[sunting | sunting sumber]
Bagian ini kosong. Anda bisa membantu dengan melengkapinya. |
Referensi[sunting | sunting sumber]
- ^ Vakil, Ravi (2017). Foundations of Algebraic Geometry.
Daftar pustaka[sunting | sunting sumber]
- Kline, M. (1972). Mathematical Thought from Ancient to Modern Times. Volume 1. Oxford University Press. ISBN 0195061357.
Bacaan lebih lanjut[sunting | sunting sumber]
- Beberapa buku teks klasik yang mendahului skema
- van der Waerden, B. L. (1945). Einfuehrung in die algebraische Geometrie. Dover.
- Hodge, W. V. D.; Pedoe, Daniel (1994). Methods of Algebraic Geometry Volume 1. Cambridge University Press. ISBN 978-0-521-46900-5. Zbl 0796.14001.
- Hodge, W. V. D.; Pedoe, Daniel (1994). Methods of Algebraic Geometry Volume 2. Cambridge University Press. ISBN 978-0-521-46901-2. Zbl 0796.14002.
- Hodge, W. V. D.; Pedoe, Daniel (1994). Methods of Algebraic Geometry Volume 3. Cambridge University Press. ISBN 978-0-521-46775-9. Zbl 0796.14003.
- Modern textbooks that do not use the language of schemes
- Garrity, Thomas; et al. (2013). Algebraic Geometry A Problem Solving Approach. American Mathematical Society. ISBN 978-0-821-89396-8.
- Griffiths, Phillip; Harris, Joe (1994). Principles of Algebraic Geometry. Wiley-Interscience. ISBN 978-0-471-05059-9. Zbl 0836.14001.
- Harris, Joe (1995). Algebraic Geometry A First Course. Springer-Verlag. ISBN 978-0-387-97716-4. Zbl 0779.14001.
- Mumford, David (1995). Algebraic Geometry I Complex Projective Varieties (edisi ke-2nd). Springer-Verlag. ISBN 978-3-540-58657-9. Zbl 0821.14001.
- Reid, Miles (1988). Undergraduate Algebraic Geometry
 . Cambridge University Press. ISBN 978-0-521-35662-6. Zbl 0701.14001.
. Cambridge University Press. ISBN 978-0-521-35662-6. Zbl 0701.14001. - Shafarevich, Igor (1995). Basic Algebraic Geometry I Varieties in Projective Space
 (edisi ke-2nd). Springer-Verlag. ISBN 978-0-387-54812-8. Zbl 0797.14001.
(edisi ke-2nd). Springer-Verlag. ISBN 978-0-387-54812-8. Zbl 0797.14001.
- Textbooks in computational algebraic geometry
- Cox, David A.; Little, John; O'Shea, Donal (1997). Ideals, Varieties, and Algorithms (edisi ke-2nd). Springer-Verlag. ISBN 978-0-387-94680-1. Zbl 0861.13012.
- Basu, Saugata; Pollack, Richard; Roy, Marie-Françoise (2006). Algorithms in real algebraic geometry. Springer-Verlag. Diarsipkan dari versi asli tanggal 2022-11-16. Diakses tanggal 2020-10-12.
- González-Vega, Laureano; Recio, Tómas (1996). Algorithms in algebraic geometry and applications. Birkhaüser.
- Elkadi, Mohamed; Mourrain, Bernard; Piene, Ragni, ed. (2006). Algebraic geometry and geometric modeling. Springer-Verlag.
- Dickenstein, Alicia; Schreyer, Frank-Olaf; Sommese, Andrew J., ed. (2008). Algorithms in Algebraic Geometry. The IMA Volumes in Mathematics and its Applications. 146. Springer. ISBN 9780387751559. LCCN 2007938208.
- Cox, David A.; Little, John B.; O'Shea, Donal (1998). Using algebraic geometry. Springer-Verlag.
- Caviness, Bob F.; Johnson, Jeremy R. (1998). Quantifier elimination and cylindrical algebraic decomposition. Springer-Verlag.
- Textbooks and references for schemes
- Eisenbud, David; Harris, Joe (1998). The Geometry of Schemes. Springer-Verlag. ISBN 978-0-387-98637-1. Zbl 0960.14002.
- Grothendieck, Alexander (1960). Éléments de géométrie algébrique. Publications Mathématiques de l'IHÉS. Zbl 0118.36206.
- Grothendieck, Alexander; Dieudonné, Jean Alexandre (1971). Éléments de géométrie algébrique. 1 (edisi ke-2nd). Springer-Verlag. ISBN 978-3-540-05113-8. Zbl 0203.23301.
- Hartshorne, Robin (1977). Algebraic Geometry. Springer-Verlag. ISBN 978-0-387-90244-9. Zbl 0367.14001.
- Mumford, David (1999). The Red Book of Varieties and Schemes Includes the Michigan Lectures on Curves and Their Jacobians (edisi ke-2nd). Springer-Verlag. ISBN 978-3-540-63293-1. Zbl 0945.14001.
- Shafarevich, Igor (1995). Basic Algebraic Geometry II Schemes and complex manifolds
 (edisi ke-2nd). Springer-Verlag. ISBN 978-3-540-57554-2. Zbl 0797.14002.
(edisi ke-2nd). Springer-Verlag. ISBN 978-3-540-57554-2. Zbl 0797.14002.
Pranala luar[sunting | sunting sumber]
- Dasar-dasar Geometri Aljabar oleh Ravi Vakil, 808 pp. Diarsipkan 2019-11-30 di Wayback Machine.
- Geometri aljabar di PlanetMath
- Terjemahan bahasa Inggris dari buku teks van der Waerden Diarsipkan 2023-03-26 di Wayback Machine.
- Dieudonné, Jean (March 3, 1972). "Sejarah Geometri Aljabar". Bicara di Departemen Matematika University of Wisconsin – Milwaukee. Diarsipkan dari versi asli tanggal 2023-05-09. Diakses tanggal 2020-10-12 – via YouTube.
- The Stacks Project Diarsipkan 2023-07-13 di Wayback Machine., sebuah buku teks open source dan referensi bekerja pada tumpukan aljabar dan geometri aljabar














![{\displaystyle k[x_{1},\dots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac6b93b5ea01d89530418e3348fcd76cf5aa18a3)



![{\displaystyle k[\mathbf {A} ^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b78e62afd3865937142f43d535b1bef37150a03)







![{\displaystyle k[V]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1741d36e6904bb3d9bb000011dfe16bfe78cc0a1)












