Aljabar homologis
Artikel atau bagian artikel ini diterjemahkan secara buruk. |
Artikel atau bagian dari artikel ini diterjemahkan dari Homological algebra di en.wikipedia.org. Terjemahannya masih terlalu kaku, kemungkinan besar karena kalimat Inggrisnya diterjemahkan kata-per-kata. Maka dari itu, terjemahan di artikel ini masih memerlukan penyempurnaan. Pengguna yang mahir dengan bahasa yang bersangkutan dipersilakan untuk menelusuri referensinya dan menyempurnakan terjemahan ini, atau Anda juga dapat ikut bergotong royong dalam ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: panduan penerjemahan artikel) |

Aljabar homologis adalah cabang matematika yang mempelajari homologi dalam pengaturan aljabar umum. Aljabar ini adalah disiplin yang relatif muda, yang asal-usulnya dapat dilacak ke penyelidikan di topologi kombinatorial (pendahulu topologi aljabar) dan aljabar abstrak (teori modul dan syzygy) pada akhir abad ke-19, terutama oleh Henri Poincaré dan David Hilbert.
Perkembangan aljabar homologis terkait erat dengan munculnya teori kategori. Pada umumnya, aljabar homologis adalah studi tentang funktor homologis dan struktur aljabar rumit yang mereka perlukan. Salah satu konsep yang cukup berguna dan ada di mana-mana dalam matematika adalah kaidah kompleks, yang dapat dipelajari melalui homologi dan kohomologi. Aljabar homologis memberi sarana untuk mengekstrak informasi yang terkandung dalam kompleks-kompleks ini dan menyajikannya dalam bentuk homologis invarian dari cincin, modul, ruang topologi, dan objek matematika 'berwujud' lainnya. Alat yang ampuh untuk melakukan hal ini disediakan oleh urutan spektral.
Dari asalnya, aljabar homologis telah memainkan peran yang sangat besar dalam topologi aljabar. Pengaruhnya secara bertahap meluas dan saat ini mencakup aljabar komutatif, geometri aljabar, teori bilangan aljabar, teori representasi, fisika matematika, operator aljabar, analisis kompleks, dan teori persamaan diferensial parsial. Teori-K adalah disiplin ilmu independen yang mengacu pada metode aljabar homologis, seperti halnya geometri nonkomutatif dari Alain Connes.
Sejarah aljabar homologis[sunting | sunting sumber]
Aljabar homologis mulai dipelajari dalam bentuknya yang paling dasar pada tahun 1800-an sebagai cabang dari topologi, tetapi tidak sampai tahun 1940-an menjadi subjek independen dengan studi objek seperti ext funktor dan tor funktor, antara lain.[1]
Kaidah kompleks dan homologi[sunting | sunting sumber]
Gagasan tentang kompleks rantai merupakan suatu gagasan yang menjadi inti bahasan dalam aljabar homologis. Suatu kompleks rantai abstrak adalah pasangan terurut dari objek pada kategori abel (umumnya digunakan kategori modul) dan morfismanya, sedemikian sehingga komposisi dua peta yang berurutan adalah nol:
Unsur disebut sebagai suatu -rantai dan morfisma dn disebut peta batas atau diferensial. Umumnya objek yang digunakan dalam kompleks rantai adalah objek pada kategori modul (atas suatu gelanggang ), tetapi dari teorema penyisipan Freyd-Mitchell sebarang kategori Abel kecil (yakni, koleksi objeknya adalah suatu himpunan) dapat disisipkan secara penuh dan faithfull ke suatu kategori modul (dalam penerapannya, bisa diambil subkategori Abel yang digunakan dalam pendefinisian kompleksnya saja). Hal ini mengakibatkan teori yang dikembangkan pada kategori modul dapat diperluas ke sebarang kategori Abel. Setiap kompleks rantai mendefinisikan dua objek, yakni siklus Zn = Ker dn dan batas Bn = Im dn+1, dengan Ker d dan Im d masing-masing menunjukkan kernel dan peta dari d. Karena komposisi dua peta batas yang berurutan adalah nol, terdapat penyisipan
Kita dapat mendefinisikan ke grup homologi Hn(C) sebagai objek kuosien dari n-siklus oleh n-batas,
Suatu kompleks rantai disebut asiklik jika semua grup homologinya adalah nol. Tentunya suatu barisan eksak merupakan suatu kompleks rantai yang asiklik.
Barisan eksak[sunting | sunting sumber]
Dalam konteks teori grup, sebuah barisan
dari grup dan homomorfisme grup disebut eksak jika citra dari setiap homomorfisme sama dengankernel dari berikutnya:
Perhatikan bahwa barisan ini mungkin terbatas atau tidak.
Definisi serupa dapat dibuat untuk struktur aljabar tertentu lainnya. Secara lebih umum, barisan eksak dapat dibentuk pada setiap kategori yang memiliki kernel dan kokernel (peta dapat didefinisikan sebagai kernel dari kokernel).
Barisan eksak pendek[sunting | sunting sumber]
Suatu barisan eksak pendek adalah barisan eksak
dengan ƒ adalah monomorfisme dan g adalah epimorfisme. Dalam hal ini, A adalah subobjek dari B , dan dari keeksakan barisannya, kita mempunyai
(dengan f(A) = im(f)).
Barisan eksak pendek pada kategori Abel juga dapat ditulis sebagai
dengan 0 mewakili objek nol pada kategori tersebut, seperti grup trivial atau ruang vektor dimensi-nol.
Barisan eksak panjang[sunting | sunting sumber]
Barisan eksak panjang adalah barisan eksak yang diindeks dengan bilangan asli.
Lima lema[sunting | sunting sumber]
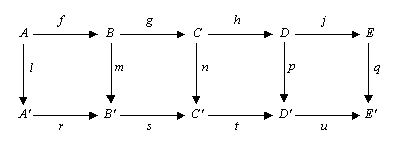
Tinjau diagram komutatif berikut di kategori abelian (seperti kategori grup abelian atau kategori ruang vektor pada suatu lapangan)
Lima lema menyatakan bahwa, jika barisnya adalah eksak, m dan p adalah isomorfisma, l adalah epimorfisme, dan q adalah monomorfisme, maka n juga merupakan isomorfisme.
Lema ular[sunting | sunting sumber]
Dalam kategori abelian (seperti kategori grup abelian atau kategori ruang vektor di atas bidang), pertimbangkan diagram komutatif:
di mana baris-barisnya adalah urutan yang tepat s dan 0 adalah objek nol. Kemudian ada urutan yang tepat terkait kernel dan kokernel dari a , b , dan c :
Selanjutnya, jika morfisme f adalah monomorphism, maka morfisme ker a → ker b , dan jika g' adalah epimorfisme, maka coker b → coker c.
Kategori Abel[sunting | sunting sumber]
Dalam matematika, kategori Abel adalah kategori di mana morfisme dan objek dapat ditambahkan dan di mana kernel dan cokernel ada dan memiliki sifat yang diinginkan. Contoh prototipe yang memotivasi dari kategori abelian adalah kategori grup abelian, Ab. Teori ini berasal dari upaya tentatif untuk menyatukan beberapa teori kohomologi oleh Alexander Grothendieck.
Lihat pula[sunting | sunting sumber]
- Abstrak nonsense, istilah untuk aljabar homologis dan teori kategori
- Derivator
- Aljabar Homotop
- Daftar topik aljabar homologis
Referensi[sunting | sunting sumber]
- ^ Weibel, Charles A. (1999). "History of Homological Algebra". History of Topology. hlm. 797–836. doi:10.1016/b978-044482375-5/50029-8. ISBN 9780444823755.
- Henri Cartan, Samuel Eilenberg, Homological algebra. With an appendix by David A. Buchsbaum. Reprint of the 1956 original. Princeton Landmarks in Mathematics. Princeton University Press, Princeton, NJ, 1999. xvi+390 pp. ISBN 0-691-04991-2
- Grothendieck, Alexander (1957). "Sur quelques points d'algèbre homologique, I". Tohoku Mathematical Journal. 9 (2): 119–221. doi:10.2748/tmj/1178244839
 .
. - Saunders Mac Lane, Homology. Reprint of the 1975 edition. Classics in Mathematics. Springer-Verlag, Berlin, 1995. x+422 pp. ISBN 3-540-58662-8
- Peter Hilton; Stammbach, U. A course in homological algebra. Second edition. Graduate Texts in Mathematics, 4. Springer-Verlag, New York, 1997. xii+364 pp. ISBN 0-387-94823-6
- Gelfand, Sergei I.; Yuri Manin, Methods of homological algebra. Translated from Russian 1988 edition. Second edition. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2003. xx+372 pp. ISBN 3-540-43583-2
- Gelfand, Sergei I.; Yuri Manin, Homological algebra. Translated from the 1989 Russian original by the authors. Reprint of the original English edition from the series Encyclopaedia of Mathematical Sciences (Algebra, V, Encyclopaedia Math. Sci., 38, Springer, Berlin, 1994). Springer-Verlag, Berlin, 1999. iv+222 pp. ISBN 3-540-65378-3
- Templat:Weibel IHA