1 − 2 + 3 − 4 + ⋯

Dalam matematika, 1 − 2 + 3 − 4 + ⋯ adalah deret tak hingga yang suku-sukunya merupakan bilangan bulat positif yang berurutan, diberi tanda plus dan minus secara bergantian satu sama lain membentuk deret selang-seling. Dengan menggunakan notasi penjumlahan sigma, jumlah m suku pertama deret tersebut dapat dinyatakan sebagai
Deret tak hingga divergen, artinya barisan jumlah parsialnya, (1, −1, 2, −2, 3, ...), tidak cenderung menuju batas berhingga. Meskipun demikian, pada pertengahan abad ke-18, Leonhard Euler menulis apa yang dia akui sebagai persamaan yang paradoks:
Penjelasan yang tepat mengenai persamaan ini baru dapat diperoleh beberapa waktu kemudian. Mulai tahun 1890, Ernesto Cesàro, Émile Borel, dan lainnya menyelidiki metode yang terdefinisi dengan baik untuk menetapkan jumlah umum ke deret yang berbeda—termasuk interpretasi baru atas upaya Euler. Banyak dari metode penjumlahan ini dengan mudah menetapkan 1 − 2 + 3 − 4 + ... sebuah "nilai" 14. Penjumlahan Cesàro adalah salah satu dari sedikit metode yang tidak menjumlahkan 1 − 2 + 3 − 4 + ..., sehingga deret tersebut merupakan contoh yang memerlukan metode yang sedikit lebih kuat, seperti penjumlahan Abel.
Deret 1 − 2 + 3 − 4 + ... berkaitan erat dengan deret Grandi 1 − 1 + 1 − 1 + .... Euler memperlakukan keduanya sebagai kasus khusus dari deret yang lebih umum 1 − 2n + 3n − 4n + ..., dimana n = 1 dan n = 0 masing-masing. Penelitian ini memperluas karyanya pada masalah Basel dan mengarah pada persamaan fungsional yang sekarang dikenal sebagai fungsi eta Dirichlet dan fungsi zeta Riemann.
Divergensi[sunting | sunting sumber]
Suku-suku deret tersebut (1, −2, 3, −4, ...) tidak mendekati 0; oleh karena itu 1 − 2 + 3 − 4 + ... menyimpang menurut istilah pengujian. Divergensi juga dapat ditunjukkan langsung dari definisinya: suatu deret tak hingga konvergen jika dan hanya jika barisan jumlah parsialnya konvergen ke limit, dalam hal ini limitnya adalah nilai deret tak hingga tersebut. Jumlah parsial dari 1 − 2 + 3 − 4 + ... adalah:[1]
Barisan penjumlahan parsial menunjukkan bahwa deret tersebut tidak konvergen ke suatu bilangan tertentu: untuk setiap limit yang diusulkan x, terdapat suatu titik yang diluarnya semua penjumlahan parsial berikutnya berada di luar interval [x−1, x+1], jadi 1 − 2 + 3 − 4 + ... menyimpang.
Jumlah parsial mencakup setiap bilangan bulat tepat satu kali—bahkan 0 jika seseorang menghitung jumlah parsial yang kosong—dan dengan demikian menetapkan keterhitungan himpunan bilangan bulat.[2]
Heuristik untuk penjumlahan[sunting | sunting sumber]
Stabilitas dan linearitas[sunting | sunting sumber]
Karena suku 1, −2, 3, −4, 5, −6, ... mengikuti pola yang sederhana, deret 1 − 2 + 3 − 4 + ... dapat dimanipulasi dengan menggeser dan suku demi suku penjumlahan untuk menghasilkan nilai numerik. Jika masuk akal untuk menulis s = 1 − 2 + 3 − 4 + ... untuk beberapa bilangan biasa s, manipulasi berikut menyatakan s = ¼:[3]

Jadi .
Meskipun 1 − 2 + 3 − 4 + ... tidak memiliki jumlah seperti biasanya, persamaan s = 1 − 2 + 3 − 4 + ... = ¼ dapat didukung sebagai jawaban paling alami jika jumlah seperti itu harus didefinisikan. Definisi digeneralisasikan dari "penjumlahan" deret divergen disebut metode penjumlahan. Ada banyak metode yang berbeda dan diharapkan metode tersebut memiliki beberapa sifat penjumlahan biasa. Apa yang sebenarnya dibuktikan oleh manipulasi di atas adalah sebagai berikut: Mengingat metode penjumlahan apa pun yang linier dan stabil serta menjumlahkan deret 1 − 2 + 3 − 4 + ..., jumlah yang dihasilkannya adalah ¼.[4] Terlebih lagi, sejak itu
metode seperti itu juga harus menjumlahkan deret Grandi sebagai 1 − 1 + 1 − 1 + ... = ½.[4]
Produk Cauchy[sunting | sunting sumber]
Pada tahun 1891, Ernesto Cesàro mengungkapkan harapannya bahwa deret divergen akan dimasukkan ke dalam kalkulus dengan tegas, dengan menyatakan, "Kita sudah menulis (1 − 1 + 1 − 1 + ...)2 = 1 − 2 + 3 − 4 + ... dan menegaskan bahwa kedua sisinya sama dengan ¼."[5] Bagi Cesàro, persamaan ini merupakan penerapan dari teorema yang telah diterbitkannya tahun sebelumnya, yang merupakan teorema pertama dalam sejarah deret divergen yang dapat dijumlahkan.[1] Detail metode penjumlahannya ada di bawah; ide utamanya adalah 1 − 2 + 3 − 4 + ... adalah hasil kali Cauchy (konvolusi diskrit) dari 1 − 1 + 1 − 1 + ... dengan 1 − 1 + 1 − 1 + ....
Hasil kali Cauchy dari dua deret tak hingga dapat didefinisikan meskipun keduanya divergen. Dalam kasus di mana an = bn = (−1)n, suku-suku hasil kali Cauchy diberikan oleh jumlah diagonal berhingga
Seri produknya kemudian
Jadi, metode penjumlahan yang mengikuti hasil kali Cauchy dari dua deret — dan menugaskan ke deret 1 − 1 + 1 − 1 + ... jumlah 1/2 — juga akan menetapkan ke deret 1 − 2 + 3 − 4 + ... jumlahnya 1/4. Dengan hasil pada bagian sebelumnya, hal ini menyiratkan adanya kesetaraan antara penjumlahan 1 − 1 + 1 − 1 + ... dan 1 − 2 + 3 − 4 + ... dengan metode yang linier, stabil, dan menghormati Cauchy produk.
Teorema Cesàro adalah contoh halus. Deret 1 − 1 + 1 − 1 + ... dapat dijumlahkan Cesàro dalam arti yang paling lemah, disebut (C, 1)-dapat dijumlahkan, dapat dijumlahkan, sedangkan 1 − 2 + 3 − 4 + ... memerlukan bentuk teorema Cesàro yang lebih kuat,[6] menjadi (C, 2)-dapat dijumlahkan. Karena semua bentuk teorema Cesàro linier dan stabil,[7] nilai penjumlahannya seperti yang dihitung di atas.
Metode khusus[sunting | sunting sumber]
Cesàro dan Hölder[sunting | sunting sumber]

Untuk mencari jumlah (C, 1) Cesàro dari 1 − 2 + 3 − 4 + ..., jika ada, kita perlu menghitung rata-rata aritmetika dari jumlah parsial deret tersebut. Jumlah sebagiannya adalah:
dan cara aritmatika dari jumlah parsial ini adalah:
Urutan mean ini tidak konvergen, jadi 1 − 2 + 3 − 4 + ... tidak dapat dijumlahkan oleh Cesàro.
Ada dua generalisasi penjumlahan Cesàro yang terkenal: yang secara konseptual lebih sederhana adalah barisan metode (H, n) untuk bilangan asli n. Jumlah (H, 1) adalah penjumlahan Cesàro, dan metode yang lebih tinggi mengulangi penghitungan mean. Di atas mean genap konvergen ke ½, sedangkan mean ganjil semuanya sama dengan 0, sehingga mean dari mean konvergen ke rata-rata 0 dan ½ yaitu ¼.[8] Jadi 1 − 2 + 3 − 4 + ... adalah (H, 2) dapat dijumlahkan menjadi ¼.
Huruf "H" adalah singkatan dari Otto Hölder, yang pertama kali membuktikan pada tahun 1882 apa yang sekarang dianggap oleh para ahli matematika sebagai hubungan antara penjumlahan Abel dan penjumlahan (H, n); 1 − 2 + 3 − 4 + ... adalah contoh pertamanya.[9] Fakta bahwa ¼ adalah (H, 2) jumlah dari 1 − 2 + 3 − 4 + ... menjamin bahwa itu adalah jumlah Abel juga; ini juga akan dibuktikan langsung di bawah ini.
Generalisasi penjumlahan Cesàro yang umum dirumuskan adalah urutan metode (C, n). Terbukti penjumlahan (C, n) dan penjumlahan (H, n) selalu memberikan hasil yang sama, namun mempunyai latar belakang sejarah yang berbeda. Pada tahun 1887, Cesàro nyaris menyatakan definisi penjumlahan (C, n), namun ia hanya memberikan sedikit contoh. Secara khusus, dia menjumlahkan 1 − 2 + 3 − 4 + ..., menjadi ¼ dengan metode yang dapat diulangi menjadi (C, n) tetapi tidak dibenarkan pada saat itu. Dia secara formal mendefinisikan metode (C, n) pada tahun 1890 untuk menyatakan teoremanya bahwa produk Cauchy dari deret yang dapat dijumlahkan (C, n) dan deret yang dapat dijumlahkan (C, m) adalah (C, m + n + 1)-dapat diringkas.[10]
Penjumlahan Habel[sunting | sunting sumber]

Dalam laporan tahun 1749, Leonhard Euler mengakui bahwa rangkaian tersebut berbeda tetapi tetap bersiap untuk menjumlahkannya:
... ketika dikatakan bahwa jumlah deret 1 − 2 + 3 − 4 + 5 − 6 dst. adalah ¼, hal itu pasti tampak paradoks. Karena dengan menjumlahkan 100 suku pada deret ini, kita mendapatkan −50, namun jumlah 101 suku menghasilkan +51, yang sangat berbeda dari ¼ dan menjadi lebih besar lagi jika jumlah sukunya ditambah. Tetapi saya telah memperhatikan di waktu sebelumnya, bahwa kata jumlah perlu diberi arti yang lebih luas ...[11]
Euler beberapa kali mengusulkan generalisasi kata "jumlah". Dalam kasus 1 − 2 + 3 − 4 + ..., gagasannya mirip dengan apa yang sekarang dikenal sebagai penjumlahan Abel:
... tidak diragukan lagi bahwa jumlah deret 1 − 2 + 3 − 4 + 5 dst. adalah ¼; karena muncul dari perluasan rumus 1⁄(1+1)2, yang nilainya tidak dapat disangkal ¼. Idenya menjadi lebih jelas dengan mempertimbangkan deret umum 1 − 2x + 3x2 − 4x3 + 5x4 − 6x5 + &c. yang muncul saat memperluas ekspresi 1⁄(1+x)2, yang mana deret ini memang sama setelah kita menetapkan x = 1.[12]
Ada banyak cara untuk melihat bahwa, setidaknya untuk nilai absolut |x| < 1, Euler benar dalam hal tersebut Kita dapat menggunakan perluasan Taylor pada ruas kanan, atau menerapkan proses pembagian panjang formal untuk polinomial. Mulai dari ruas kiri, kita dapat mengikuti heuristik umum di atas dan mencoba mengalikan dengan (1 + x) dua kali atau mengkuadratkan deret geometri 1 − x + x2 − .... Euler juga sepertinya menyarankan untuk membedakan suku deret terakhir berdasarkan istilah.[13]
Dalam pandangan modern, fungsi pembangkit 1 − 2x + 3x2 − 4x3 + ... tidak mendefinisikan suatu fungsi pada x = 1, sehingga nilai tersebut tidak dapat disubstitusikan begitu saja ke dalam ekspresi yang dihasilkan. Karena fungsinya terdefinisi untuk semua |x| < 1, kita masih dapat mengambil limitnya ketika x mendekati 1, dan ini adalah definisi dari jumlah Abel:
Euler dan Borel[sunting | sunting sumber]
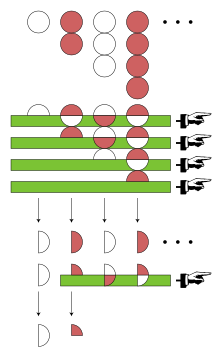
Euler menerapkan teknik lain pada deret tersebut: transformasi Euler, salah satu penemuannya sendiri. Untuk menghitung transformasi Euler, dimulai dengan barisan suku positif yang membentuk deret bolak-balik—dalam hal ini 1, 2, 3, 4, .... Elemen pertama barisan ini diberi label a0.
Selanjutnya diperlukan barisan selisih maju antara 1, 2, 3, 4, ...; ini hanya 1, 1, 1, 1, .... Elemen pertama barisan ini diberi label Δa0. Transformasi Euler juga bergantung pada selisih selisih, dan iterasi yang lebih tinggi, namun semua selisih maju antara 1, 1, 1, 1, ... adalah 0. Transformasi Euler dari 1 − 2 + 3 − 4 + ... adalah kemudian didefinisikan sebagai
Dalam terminologi modern, dikatakan bahwa 1 − 2 + 3 − 4 + ... adalah Euler dapat dijumlahkan menjadi ¼..
Penjumlahan Euler juga menyiratkan penjumlahan Borel, dengan nilai penjumlahan yang sama, seperti pada umumnya.[14]
Pemisahan timbangan[sunting | sunting sumber]
Saichev dan Woyczyński sampai pada 1 − 2 + 3 − 4 + ... = ¼ dengan hanya menerapkan dua prinsip fisik: relaksasi yang sangat kecil dan pemisahan timbangan. Tepatnya, prinsip-prinsip ini mengarahkan mereka untuk mendefinisikan kelompok besar "metode penjumlahan φ", yang semuanya menjumlahkan rangkaiannya menjadi ¼:
- Jika φ(x) adalah suatu fungsi yang turunan pertama dan kedua kontinu dan dapat diintegralkan pada (0, ∞), sehingga φ(0) = 1 dan limit dari φ(x) dan xφ(x) di +∞ keduanya adalah 0, lalu[15]
Hasil ini menggeneralisasi penjumlahan Abel, yang diperoleh dengan membiarkan φ(x) = exp(−x). Pernyataan umum dapat dibuktikan dengan memasangkan suku-suku dalam deret tersebut pada m dan mengubah persamaan tersebut menjadi integral Riemann. Untuk langkah terakhir, pembuktian yang sesuai untuk 1 − 1 + 1 − 1 + ... menerapkan teorema nilai purata, tetapi di sini diperlukan bentuk teorema Taylor Lagrange yang lebih kuat.
Generalisasi[sunting | sunting sumber]

Hasil kali Cauchy rangkap tiga dari 1 − 1 + 1 − 1 + ... adalah 1 − 3 + 6 − 10 + ..., deret bilangan segitiga berselang-seling; jumlah Abel dan Eulernya adalah ⅛.[16] Hasil kali Cauchy empat kali lipat dari 1 − 1 + 1 − 1 + ... adalah 1 − 4 + 10 − 20 + ..., deret bilangan tetrahedral yang berselang-seling, yang jumlah Abelnya adalah 1⁄16.
Generalisasi lain dari 1 − 2 + 3 − 4 + ... dalam arah yang sedikit berbeda adalah deret 1 − 2n + 3n − 4n + ... untuk nilai n lainnya. Untuk bilangan bulat positif n, deret ini mempunyai jumlah Abel sebagai berikut:[17] dimana Bn adalah bilangan Bernoulli. Bahkan untuk n, ini direduksi menjadi yang dapat diartikan menyatakan bahwa nilai genap negatif dari fungsi zeta Riemann adalah nol. Jumlah ini menjadi bahan ejekan khusus oleh Niels Henrik Abel pada tahun 1826:
Seri divergen sepenuhnya merupakan pekerjaan iblis, dan sayang sekali jika ada yang berani menemukan bukti apa pun mengenainya. Seseorang dapat memperoleh apa yang diinginkannya jika ia menggunakannya, dan hal-hal itulah yang telah menciptakan begitu banyak ketidakbahagiaan dan begitu banyak paradoks. Adakah yang bisa memikirkan hal yang lebih mengerikan daripada mengatakan hal itu
dimana n adalah bilangan positif. Ini sesuatu untuk ditertawakan, teman-teman.[18]
Guru Cesàro, Eugène Charles Catalan, juga meremehkan deret divergen. Di bawah pengaruh Catalan, Cesàro awalnya menyebut "rumus konvensional" untuk 1 − 2n + 3n − 4n + ... sebagai "persamaan yang tidak masuk akal", dan pada tahun 1883 Cesàro mengungkapkan pandangan umum pada saat itu bahwa rumus tersebut salah tetapi tetap saja entah bagaimana berguna secara formal. Terakhir, dalam Sur la multiplication des séries tahun 1890, Cesàro mengambil pendekatan modern yang dimulai dari definisi.[19]
Deret tersebut juga dipelajari untuk nilai non-integer n; ini membentuk fungsi eta Dirichlet. Bagian dari motivasi Euler mempelajari deret yang berkaitan dengan 1 − 2 + 3 − 4 + ... adalah persamaan fungsional fungsi eta, yang mengarah langsung ke persamaan fungsional fungsi zeta Riemann. Euler telah menjadi terkenal karena menemukan nilai-nilai fungsi ini pada bilangan bulat genap positif (termasuk masalah Basel), dan dia juga mencoba menemukan nilai-nilai pada bilangan bulat ganjil positif (termasuk konstanta Apéry), sebuah masalah yang masih sulit dipahami hingga saat ini. Fungsi eta khususnya lebih mudah ditangani dengan metode Euler karena deret Dirichletnya dapat dijumlahkan Abel di mana saja; deret Dirichlet fungsi zeta jauh lebih sulit untuk dijumlahkan jika ia menyimpang.[20] Misalnya, pasangan dari 1 − 2 + 3 − 4 + ... dalam fungsi zeta adalah deret tak bolak-balik 1 + 2 + 3 + 4 + ⋯, yang memiliki penerapan mendalam dalam fisika modern namun membutuhkan lebih banyak kekuatan metode untuk menjumlahkan.
Lihat juga[sunting | sunting sumber]
Referensi[sunting | sunting sumber]
- ^ a b Hardy 1949, hlm. 8.
- ^ Beals 2004, hlm. 23.
- ^ Hardy 1949, hlm. 6 menyajikan penurunan ini bersamaan dengan evaluasi deret Grandi 1 − 1 + 1 − 1 + ....
- ^ a b Hardy 1949, hlm. 6.
- ^ Ferraro 1999, hlm. 130.
- ^ Hardy 1949, hlm. 3; Weidlich 1950, hlm. 52–55.
- ^ Alabdulmohsin 2018.
- ^ Hardy 1949, hlm. 9. Untuk detail perhitungan selengkapnya, lihat Weidlich 1950, hlm. 17–18.
- ^ Ferraro 1999, hlm. 118; Tucciarone 1973, hlm. 10. Ferraro mengkritik penjelasan Tucciarone (p. 7) tentang bagaimana Hölder sendiri memikirkan hasil umum, tetapi penjelasan kedua penulis mengenai perlakuan Hölder terhadap 1 − 2 + 3 − 4 + ... serupa.
- ^ Ferraro 1999, hlm. 123–128.
- ^ Euler, Willis & Osler 2006, hlm. 2. Meskipun makalah tersebut ditulis pada tahun 1749, namun baru diterbitkan pada tahun 1768.
- ^ Euler, Willis & Osler 2006, hlm. 3, 25.
- ^ Misalnya, Lavine 1994, hlm. 23 mendukung perpecahan yang panjang tetapi tidak melaksanakannya; Vretblad 2003, hlm. 231 menghitung produk Cauchy. Nasihat Euler tidak jelas; lihat Euler, Willis & Osler 2006, hlm. 3, 26. John Baez bahkan menyarankan metode teori kategori yang melibatkan himpunan lonjong perkalian dan osilator harmonis kuantum. Baez, John C. Euler's Proof That 1 + 2 + 3 + ... = −1/12 (PDF). Diarsipkan 2017-10-13 di Wayback Machine. math.ucr.edu (19 Desember 2003). Diakses pada 11 Maret 2007.
- ^ Shawyer & Watson 1994, hlm. 32.
- ^ Saichev & Woyczyński 1996, hlm. 260–264.
- ^ Kline 1983, hlm. 313.
- ^ Hardy 1949, hlm. 3; Knopp 1990, hlm. 491.
- ^ Grattan-Guinness 1970, hlm. 80. Lihat Markusevič 1967, hlm. 48, untuk terjemahan berbeda dari bahasa Prancis asli; nadanya tetap sama.
- ^ Ferraro 1999, hlm. 120–128.
- ^ Euler, Willis & Osler 2006, hlm. 20–25.
Daftar pustaka[sunting | sunting sumber]
- Alabdulmohsin, Ibrahim M. (2018). "Analytic summability theory". Summability Calculus. Springer International Publishing. hlm. 65–91. doi:10.1007/978-3-319-74648-7_4. ISBN 978-3-319-74647-0.
- Beals, Richard (2004). Analysis: An Introduction. Cambridge UP. ISBN 978-0-521-60047-7.
- Davis, Harry F. (Mei 1989). Fourier Series and Orthogonal Functions. Dover. ISBN 978-0-486-65973-2.
- Euler, Leonhard; Willis, Lucas; Osler, Thomas J. (2006). "Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series". The Euler Archive. Diakses tanggal 2007-03-22. Originally published as Euler, Leonhard (1768). "Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques". Mémoires de l'Académie des Sciences de Berlin. 17: 83–106.
- Ferraro, Giovanni (Juni 1999). "The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics". Archive for History of Exact Sciences. 54 (2): 101–135. doi:10.1007/s004070050036.
- Grattan-Guinness, Ivor (1970). The development of the foundations of mathematical analysis from Euler to Riemann
 . MIT Press. ISBN 978-0-262-07034-8.
. MIT Press. ISBN 978-0-262-07034-8. - Hardy, G. H. (1949). Divergent Series. Clarendon Press. xvi+396. ISBN 978-0-8218-2649-2. LCCN 49005496. MR 0030620. OCLC 808787. 2nd Ed. published by Chelsea Pub. Co., 1991. LCCN 91-75377. ISBN 0-8284-0334-1.
- Kline, Morris (November 1983). "Euler and Infinite Series". Mathematics Magazine. 56 (5): 307–314. CiteSeerX 10.1.1.639.6923
 . doi:10.2307/2690371. JSTOR 2690371.
. doi:10.2307/2690371. JSTOR 2690371. - Knopp, Konrad (1990). Theory and Application of Infinite Series. New York: Dover Publications. ISBN 0486661652. LCCN 89071388.
- Lavine, Shaughan (1994). Understanding the Infinite. Harvard UP. ISBN 978-0-674-92096-5.
- Markusevič, Aleksej Ivanovič (1967). Series: fundamental concepts with historical exposition (edisi ke-English translation of 3rd revised edition (1961) in Russian). Delhi, India: Hindustan Pub. Corp. hlm. 176. LCCN sa68017528. OCLC 729238507. Author also known as A. I. Markushevich and Alekseï Ivanovitch Markouchevitch. Also published in Boston, Mass by Heath with OCLC 474456247. Additionally, OCLC 208730, OCLC 487226828.
- Saichev, A. I.; Woyczyński, W. A. (1996). Distributions in the Physical and Engineering Sciences, Volume 1. Birkhaüser. ISBN 978-0-8176-3924-2.
- Shawyer, Bruce; Watson, Bruce (1994). Borel's Methods of Summability: Theory and Application. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York. ISBN 0-19-853585-6. MR 1320266.
- Tucciarone, John (Januari 1973). "The development of the theory of summable divergent series from 1880 to 1925". Archive for History of Exact Sciences. 10 (1–2): 1–40. doi:10.1007/BF00343405.
- Vretblad, Anders (2003). Fourier Analysis and Its Applications. Springer. ISBN 978-0-387-00836-3.
- Weidlich, John E. (Juni 1950). Summability methods for divergent series. Stanford M.S. theses. OCLC 38624384.




![{\displaystyle {\begin{alignedat}{5}4s&=&&(1-2+3-\cdots )\ \ &&{}+(1-2+3-4+\cdots )&&{}+(1-2+3-4+\cdots )&&{}+(1-2+3-4+\cdots )\\&=&&(1-2+3-\cdots )&&+1{}+(-2+3-4+\cdots )\ \ &&{}+1+(-2+3-4+\cdots )\ \ &&{}+1-2+(3-4+\cdots )\\&=\ 1+{}&&(1-2+3-\cdots )&&{}+(-2+3-4+\cdots )&&{}+(-2+3-4+\cdots )&&{}+(3-4+5-\cdots )\\&=\ 1+{}[\ &&(1-2-2+3)&&{}+(-2+3+3-4)&&{}+(3-4-4+5)&&{}+\cdots \ ]\\&=\ 1+{}[\ &&0+0+0+\cdots \ ]\\4s&=\ 1\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0ee86ad2b2600e0208b9e2802b4c3f41f4508e7)

![{\displaystyle {\begin{alignedat}{5}2s&=&&(1-2+3-4+\cdots )\ \ &&{}+(1-2+3-4+5-\cdots )\\&=&&1{}+(-2+3-4+\cdots )\ \ &&{}+1-2+(3-4+5-\cdots )\\&=\ 0+{}&&(-2+3-4+\cdots )&&{}+(3-4+5-\cdots )\\&=\ 0+{}[\ &&(-2+3)\quad {}+(3-4)&&{}+(-4+5)\quad +\cdots \ ]\\2s&=\ &&1-1+1-1+\cdots \end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a46eb3618f411e9f0d30d9d93853fa2b547435f9)








