Bilangan Fibonacci
Artikel ini perlu dikembangkan dari artikel terkait di Wikipedia bahasa Inggris. (Februari 2024)
klik [tampil] untuk melihat petunjuk sebelum menerjemahkan.
|
Dalam matematika, bilangan Fibonacci adalah sebuah bilangan yang di mana setiap bilangannya adalah jumlah dari dari dua bilangan sebelumnya. Bilangan yang merupakan bagian dari bilangan Fibonacci dikenal sebagai deret Fibonacci, biasanya dilambangkan Fn . Bilangannya biasanya dimulai dari 0 dan 1, meskipun beberapa penulis memulai urutannya dari 1 dan 1 atau kadang-kadang (seperti yang dilakukan Fibonacci) dari 1 dan 2. Dimulai dari 0 dan 1, bilangannya dimulai
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ....[1]
Dalam matematika, bilangan Fibonacci adalah barisan yang didefinisikan secara rekursif sebagai berikut:
Barisan bilangan Fibonacci dapat dinyatakan sebagai berikut:
dengan
- adalah bilangan Fibonacci ke-n
- dan adalah penyelesaian persamaan
Perbandingan antara dengan hampir selalu sama untuk sebarang nilai n dan mulai nilai n tertentu, perbandingan ini nilainya tetap. Perbandingan itu disebut rasio emas yang nilainya mendekati 1,618.
Definisi[sunting | sunting sumber]

Bilangan Fibonacci dapat didefinisikan oleh relasi perulangan[2]
Berdasarkan beberapa definisi lama, nilai dihilangkan, jadi bilangan tersebut dimulai dengan dan perulangan valid untuk n > 2.[3][4]
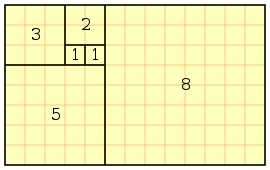
20 bilangan Fn Fibonacci pertama adalah:[5]
F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15 F16 F17 F18 F19 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181
Asal mula[sunting | sunting sumber]
Berdasarkan buku The Art of Computer Programming karya Donald E. Knuth, barisan ini pertama kali dijelaskan oleh matematikawan India, Gopala dan Hemachandra pada tahun 1150, ketika menyelidiki berbagai kemungkinan untuk memasukkan barang-barang ke dalam kantong.
Eropa[sunting | sunting sumber]

Bilangan Fibonacci pertama kali muncul pada buku Liber Abaci (The Book of Calculation, 1202) oleh Fibonacci[6][7] yang di mana digunakan untuk menghitung pertumbuhan populasi kelinci.[8][9] Fibonacci mempertimbangkan pertumbuhan populasi kelinci yang ideal (secara biologis tidak realistis), berasumsi bahwa: seekor sepasang kelinci yang baru lahir diternakkan di ladang; setiap pasangan kawin pada umur satu bulan, dan pada akhir bulan kedua selalu menghasilkan sepasang kelinci lagi; dan kelinci tidak akan mati, tetapi terus berkembang biak selamanya. Fibonacci mengajukan teka-teki: berapa banyak pasangan yang akan ada dalam satu tahun?
- Pada akhir di bulan pertama, mereka kawin, tapi masih ada 1 pasangan saja.
- Pada akhir bulan kedua mereka menghasilkan pasangan baru, jadi ada 2 pasangan di lapangan.
- Pada akhir bulan ketiga, pasangan awal menghasilkan pasangan kedua, tapi pasangan kedua hanya kawin selama sebulan, jadi totalnya ada 3 pasangan.
- Pada akhir bulan keempat, pasangan asli telah menghasilkan pasangan baru lagi, dan pasangan yang lahir dua bulan lalu juga menghasilkan pasangan pertamanya, sehingga menjadi 5 pasangan.
Pada akhir bulan ke-n, jumlah pasang kelinci sama dengan jumlah pasangan dewasa (yaitu jumlah pasangan dalam bulan n – 2) ditambah jumlah dari pasangan yang hidup bulan lalu (bulan n – 1). Jumlah pada n-th bulan adalah bilangan Fibonacci ke-n.[10]
Nama "Deret Fibonacci" pertama kali digunakan oleh ahli teori bilangan abad ke-19 Édouard Lucas.[11]

Relasi terhadap rasio emas[sunting | sunting sumber]
Identifikasi[sunting | sunting sumber]
Rumus Binet memberikan bukti bahwa bilangan bulat positif x adalah sebuah bilangan Fibonacci jika dan hanya jika setidaknya salah satu dari atau adalah persegi sempurna.[12] Hal ini karena rumus Binet yang dapat dituliskan sebagai , dapat dikalikan dengan dan diselesaikan sebagai persamaan kuadrat di melalui rumus kuadrat:
Khususnya, sisi kiri adalah persegi sempurna.
Identitas lain[sunting | sunting sumber]
Banyak bentuk lain yang dapat diperoleh dengan menggunakan berbagai metode. Inilah beberapa di antaranya:[13]
Identitas Cassini dan Catalan[sunting | sunting sumber]
Identitas Cassini menyatakan bahwa
Identitas d'Ocagne[sunting | sunting sumber]
Lebih umumnya,[13]
Referensi[sunting | sunting sumber]
Catatan kaki penjelas[sunting | sunting sumber]
Kutipan[sunting | sunting sumber]
- ^ Sloane, N.J.A. (ed.). "Sequence A000045 (Fibonacci numbers: F(n) = F(n-1) + F(n-2) with F(0) = 0 and F(1) = 1)". On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Lucas 1891, hlm. 3.
- ^ Beck & Geoghegan 2010.
- ^ Bóna 2011, hlm. 180.
- ^ Kesalahan pengutipan: Tag
<ref>tidak sah; tidak ditemukan teks untuk ref bernamaoeis - ^ Sigler 2002, hlm. 404–405.
- ^ "Fibonacci's Liber Abaci (Book of Calculation)", The University of Utah, 13 December 2009, diakses tanggal 28 November 2018
- ^ Hemenway, Priya (2005), Divine Proportion: Phi In Art, Nature, and Science, New York: Sterling, hlm. 20–21, ISBN 1-4027-3522-7
- ^ Knott, Ron (25 September 2016), "The Fibonacci Numbers and Golden section in Nature – 1", University of Surrey, diakses tanggal 27 November 2018
- ^ Knott, Ron, Fibonacci's Rabbits, University of Surrey Faculty of Engineering and Physical Sciences
- ^ Gardner, Martin (1996), Mathematical Circus, The Mathematical Association of America, hlm. 153, ISBN 978-0-88385-506-5,
It is ironic that Leonardo, who made valuable contributions to mathematics, is remembered today mainly because a 19th-century French number theorist, Édouard Lucas... attached the name Fibonacci to a number sequence that appears in a trivial problem in Liber abaci
- ^ Gessel, Ira (October 1972), "Fibonacci is a Square" (PDF), The Fibonacci Quarterly, 10 (4): 417–19, diakses tanggal April 11, 2012
- ^ a b (Inggris) Weisstein, Eric W., "Fibonacci Number", MathWorld
Kutipan ilmiah[sunting | sunting sumber]
- Ball, Keith M (2003), "8: Fibonacci's Rabbits Revisited", Strange Curves, Counting Rabbits, and Other Mathematical Explorations, Princeton, NJ: Princeton University Press, ISBN 978-0-691-11321-0.
- Beck, Matthias; Geoghegan, Ross (2010), The Art of Proof: Basic Training for Deeper Mathematics, New York: Springer, ISBN 978-1-4419-7022-0.
- Bóna, Miklós (2011), A Walk Through Combinatorics (edisi ke-3rd), New Jersey: World Scientific, ISBN 978-981-4335-23-2.
- Borwein, Jonathan M.; Borwein, Peter B. (July 1998), Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity, Wiley, hlm. 91–101, ISBN 978-0-471-31515-5
- Lemmermeyer, Franz (2000), Reciprocity Laws: From Euler to Eisenstein, Springer Monographs in Mathematics, New York: Springer, ISBN 978-3-540-66957-9.
- Livio, Mario (2003) [2002], The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (edisi ke-First trade paperback), New York City: Broadway Books, ISBN 0-7679-0816-3
- Lucas, Édouard (1891), Théorie des nombres (dalam bahasa Prancis), 1, Paris: Gauthier-Villars.
- Sigler, L. E. (2002), Fibonacci's Liber Abaci: A Translation into Modern English of Leonardo Pisano's Book of Calculation, Sources and Studies in the History of Mathematics and Physical Sciences, Springer, ISBN 978-0-387-95419-6
Lihat pula[sunting | sunting sumber]
Pranala luar[sunting | sunting sumber]
- The Golden Mean and the Physics of Aesthetics
- The Golden Section: Phi Diarsipkan 2006-12-05 di Wayback Machine.
- Menghitung bilangan Fibonacci pada Mesin Turing Diarsipkan 2005-02-06 di Wayback Machine.
- Hemachandra's application to Sanskrit poetry Diarsipkan 2012-07-16 di Wayback Machine.
- Deret Fibonacci Diarsipkan 2005-01-22 di Wayback Machine.
- Representasi Bilangan Bulat menggunakan bilangan Fibonacci Diarsipkan 2007-10-30 di Wayback Machine.






























