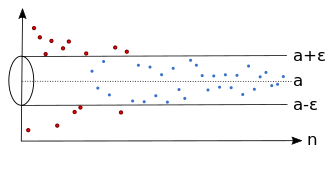
Limit barisan

| n | n sin(1/n) |
|---|---|
| 1 | 0.841471 |
| 2 | 0.958851 |
| ... | |
| 10 | 0.998334 |
| ... | |
| 100 | 0.999983 |
Semakin bilangan bulat positif membesar tanpa batas, nilai menjadi semakin dekat menuju . Dapat dikatakan bahwa "limit barisan sama dengan ."
Dalam matematika, limit barisan adalah nilai yang didekati oleh suku-suku barisan ketika nomor urut suku-sukunya semakin membesar. Limit barisan seringkali dilambangkan dengan (yaitu, ).[1] Jika suatu barisan mempunyai limit, barisan itu disebut konvergen. Barisan yang tidak konvergen disebut divergen.[2] Limit barisan dikatakan sebagai gagasan landasan seluruh analisis matematika.[3]
Limit dapat ditentukan pada ruang metrik atau ruang topologi, tetapi biasanya pertama kali ditemukan dalam bilangan real.
Sejarah[sunting | sunting sumber]
Filsuf Yunani Zeno dari Elea terkenal karena merumuskan paradoks yang melibatkan proses-proses limit.
Leucippus, Democritus, Antiphon, Eudoksos, dan Archimedes mengembangkan metode penghabis, yakni menggunakan barisan hampiran tak hingga untuk mencari luas atau volume. Archimedes berhasil menjumlahkan apa yang sekarang disebut deret geometrik.
Newton membincangkan deret dalam karyanya Analysis with infinite series (ditulis pada tahun 1669, diedarkan dalam bentuk manuskrip, diterbitkan pada tahun 1711), Method of fluxions and infinite series (ditulis tahun 1671, diterbitkan dalam terjemahan bahasa Inggris tahun 1736, buku asal yang berbahasa Latin diterbitkan lama kemudian) dan Tractatus de Quadratura Curvarum (ditulis tahun 1693, diterbitkan tahun 1704 sebagai Lampiran bagi karya Optiks). Dalam karya terakhir, Newton menganggap ekspansi binomial , yang kemudian dia linierisasi dengan mengambil nilai limit karena o cenderung ke 0.
Pada abad ke-18, matematikawan seperti Euler berhasil menjumlahkan beberapa deret divergen dengan berhenti pada saat yang tepat; mereka tidak terlalu peduli apakah ada limit, asalkan bisa dihitung. Di akhir abad ini, Lagrange dalam Théorie des fonctions analytiques (1797) berpendapat bahwa kurangnya ketelitian menghalangi perkembangan lebih lanjut dalam kalkulus. Gauss dalam buku latihannya tentang deret hipergeometrik (1813) untuk pertama kalinya diselidiki, secara teliti, syarat apa yang cukup menjamin kekonvergenan suatu deret.
Definisi modern dari suatu limit (untuk suatu ε terdapat suatu indeks N sedemikian sehingga...) diberikan oleh Bernhard Bolzano (Der binomische Lehrsatz, Prague 1816, kurang dapat perhatikan pada saat itu), dan oleh Karl Weierstrass pada tahun 1870an.
Limit barisan bilangan[sunting | sunting sumber]
Misalkan suatu barisan tak hingga dari bilangan (riil atau kompleks). Suatu bilangan adalah limit dari apabila suku-suku barisan semakin mendekati saat membesar tanpa batas[4]. Jika adalah limit dari barisan maka barisan tersebut dikatakan konvergen ke atau mempunyai limit atau memusat pada bilangan [5]. Barisan yang tidak mempunyai limit dikatakan divergen.
Secara lebih tepat, suatu bilangan adalah limit dari barisan bilangan tak hingga apabila berlaku[6]
yakni, untuk sebarang bilangan positif , dapat ditentukan yang bergantung pada sedemikian rupa, sehingga untuk semua bilangan bulat positif berlaku , dengan melambangkan nilai mutlak untuk bilangan riil dan nilai modulus untuk bilangan kompleks[7][8].
Notasi untuk barisan yang konvergen menuju ditulis sebagai . Terkadang juga ditulis [9].
-
Contoh barisan yang konvergen ke .
-
Untuk sebarang yang dipilih, terdapat bilangan bulat sedemikian sehingga seluruh nilai barisan dari suku ke- sampai seterusnya berada di lingkungan .
-
Untuk nilai, yang lain, akan terdapat pula bilangan bulat , bersesuaian dengan nilai tersebut, sedemikian sehingga barisan dari suku ke- sampai seterusnya itu berada di dalam lingkungan .
-
Untuk setiap , hanya terdapat sebanyak hingga anggota barisan di luar lingkungan .
Limit tak sebenarnya[sunting | sunting sumber]
Suatu barisan dikatakan mendekati takhingga, ditulis atau , jika untuk setiap bilangan real , terdapat suatu bilangan bulat sedemikian sehingga untuk setiap , ; yaitu, suku barisan pada akhirnya akan lebih besar daripada sembarang yang dipilih. Dengan cara yang serupa, jika untuk setiap , terdapat suatu sehingga untuk setiap , .
Jika suatu barisan cenderung ke takhingga atau negatif takhingga, maka barisan tersebut adalah divergen. Namun, suatu barisan divergen bukanlah syarat perlu untuk suatu barisan mendekati takhingga atau negatif takhingga, seperti barisan tanda . Perilaku limit barisan divergen yang terbatas dapat ditelaah dengan memperhatikan barisan bagiannya, limit superior dan inferior, serta titik limit.
Contoh-contoh[sunting | sunting sumber]

- Jika untuk suatu konstanta c, maka .[bukti 1][10]
- Jika , maka .[bukti 2][10]
- Jika untuk genap, dan untuk ganjil, maka . (Kenyataan bahwa apabila ganjil tidak penting.)
- Diberikan sebarang bilangan real; suatu barisan yang konvergen menuju suatu bilangan dapat dengan mudah dibangun dengan mengambil hampiran desimal. Misal, barisan konvergen menuju . Perhatikan bahwa representasi desimal adalah limit dari barisan sebelumnya, yang ditentukan oleh .
- Limit suatu barisan tidak selalu dapat ditemukan dengan mudah. Dua contohnya adalah (limitnya adalah bilangan e) dan purata aritmetika–geometrik (limitnya 13,458...). Teorema apit sering kali berguna dalam pencarian limit barisan yang sebegini.
Sifat-sifat[sunting | sunting sumber]
- Limit suatu barisan, apabila ada, adalah tunggal.
- Misal diketahui dua barisan konvergen dan ,
- barisan hasil jumlah atau hasil pengurangan kedua barisan tersebut adalah konvergen pula, dan berturut-turut limitnya adalah jumlah atau selilsish limit dua barisan yang diketahui.
- barisan hasil kali kedua barisan tersebut adalah konvergen pula, dan limitnya adalah perkalian limit dua barisan yang diketahui.
- apabila , barisan hasil bagi kedua barisan tersebut adalah konvergen pula, dan limitnya adalah perkalian limit dua barisan yang diketahui.
- Jika untuk semua lebih besar dari suatu , maka .
- Jika untuk semua , dan , maka . (teorema apit)
- Jika suatu barisan mempunyai limit, maka barisan itu terbatas.
- Jika suatu barisan terbatas dan monoton, maka barisan itu mempunyai limit (teorema kekonvergenan barisan monoton).
- Suatu barisan adalah konvergen jika dan hanya jika setiap barisan bagiannya konvergen.
Ruang metrik[sunting | sunting sumber]
Definisi[sunting | sunting sumber]
Suatu titik dalam ruang metrik adalah limit dari barisan jika untuk sembarang nilai , terdapat nilai sedemikian rupa, sehingga untuk setiap nilai , . Definisi ini berlaku juga untuk bilangan real dengan dan .
Sifat-sifat[sunting | sunting sumber]
- Untuk suatu fungsi kontinu f, jika maka . Faktanya, fungsi f kontinu jika dan hanya jika untuk sembarang barisan menuju suatu limit berlaku .
- Limit barisan, apabila ada, itu tunggal. Karena dua titik berbeda terpisahkan oleh suatu jarak positif, jadi untuk kurang dari setengah jarak ini, suku-suku barisan tidak bisa berada dalam jarak dari kedua titik tersebut.
Barisan Cauchy[sunting | sunting sumber]

Barisan Cauchy adalah barisan yang sukunya bagian akhir menjadi berdekatan secara acak, setelah cukup banyak istilah awal yang dihapus akan dikembalikan. Gagasan tentang barisan Cauchy penting dalam studi barisan di ruang metrik, dan, khususnya, di analisis riil. Salah satu hasil yang sangat penting dalam analisis nyata adalah Kriteria Cauchy untuk kekonvergenan barisan: barisan bilangan real adalah konvergen jika dan hanya jika itu adalah barisan Cauchy. Hal ini tetap berlaku di ruang metrik lengkap.
Definisi dalam bilangan hiperreal[sunting | sunting sumber]
Definisi batas menggunakan bilangan hiperreal menggunakan intuisi bahwa untuk nilai indeks yang "sangat besar", istilah terkait adalah "sangat dekat" dengan batas. Lebih tepatnya, barisan yang nyata cenderung L jika untuk setiap tak terbatas hipernatural H, syarat xH is sangat dekat dengan L (yaitu, perbedaan nilai xH − L adalah infinitesimal). Setara, L adalah bagian standar dari xH
Jadi, limitnya bisa ditentukan dengan rumus
dengan limit tersebut ada jika dan hanya jika ruas kanan tidak bergantung pada pemilihan dari suatu takhingga H.
Lihat pula[sunting | sunting sumber]
- Limit fungsi – titik untuk yang fungsi konvergen dalam topologi
- Titik limit – suatu titik x dalam suatu ruang topologis, semua lingkungan berisi beberapa titik dalam diberikan suatu himpunan bagian yang berbeda dari x.
- Limit atas dan limit bawah
- Mode kekonvergenan
- Limit jaring — suatu jaring rampat topologis dari suatu barisan
- Limit teoretik himpunan
- Aturan gesekan
- Limit berurut bagian
Catatan[sunting | sunting sumber]
- ^ E., Hutahaean, (1983). Kalkulus Diferensial dan Integral I. Jakarta: PT Gramedia. OCLC 949729321.
- ^ Stewart, James (2001). Kalkulus. Diterjemahkan oleh Drs. I Nyoman Susila, M.Sc. dan Hendra Gunawan, Ph.D. Jakarta: Erlangga. ISBN 979-688-221-3.
- ^ Courant (1961), p. 29.
- ^ Ayres, Frank; Mendelson, Elliot (2006). Kalkulus. Diterjemahkan oleh Nur Danarjaya, M.Sc. Jakarta: Penerbit Erlangga.
- ^ Panggabean, A.B (2014). Kalkulus Tingkat Lanjut. Yogyakarta: Graha Ilmu. ISBN 978-602-262-264-2.
- ^ Martono, Koko (2000). Sari Informasi Fungsi Kompleks. Bandung: Himpunan Pegawai Matematika ITB.
- ^ Handali, Daniel; Pamuntjak, Rasyidin J. (2004). Kalkulus Perubah Banyak. Bandung: Penerbit ITB. ISBN 979-3507-12-8.
- ^ Dedy, Endang; Sumiyaty, Encum (2019). Fungsi Variabel Kompleks. Jakarta: PT Bumi Aksara. ISBN 978-602-444-713-7.
- ^ Endang Cahya; Makbul Muksar (2011). Analisis Real. Tanggerang Selatan: Universitas Terbuka. ISBN 978-979-011-674-0.
- ^ a b "Limit of Sequences | Brilliant Math & Science Wiki". brilliant.org (dalam bahasa Inggris Amerika). Diakses tanggal 2020-08-18.
Bukti[sunting | sunting sumber]
- ^ Bukti: Pilih nilai . Untuk setiap ,
- ^ Bukti: Pilih + 1 (fungsi lantai). Untuk setiap , .
Referensi[sunting | sunting sumber]
- Courant, Richard (1961). "Volume Kalkulus Diferensial dan Integral I", Blackie & Son, Ltd., Glasgow.
- Frank Morley dan James Harkness A treatise on the theory of functions (New York: Macmillan, 1893)
Pranala luar[sunting | sunting sumber]
- Hazewinkel, Michiel, ed. (2001) [1994], "Limit", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
- A history of the calculus, including limits