Laju cahaya
 Sinar matahari memerlukan sekitar 8 menit 17 detik untuk melalui jarak rata-rata dari permukaan Matahari ke Bumi. | |
| Nilai eksak | |
|---|---|
| meter per detik | 299.792.458 |
| panjang Planck per waktu Planck (yaitu, satuan Planck) | 1 |
| Nilai kira-kira (sampai tiga angka pentingnya.) | |
| kilometer per jam | 1,08 miliar (1,08×109) |
| mil per detik | 186.000 |
| mil per jam | 671 juta (6,71×108) |
| satuan astronomi per hari | 173[catatan 1] |
| parsec per tahun | 0,307[catatan 2] |
| Perkiraan waktu tempuh cahaya | |
| Jarak | Waktu |
| satu kaki | 1,0 nanodetik |
| satu meter | 3,3 nanodetik |
| dari orbit geostasioner ke Bumi | 119 milidetik |
| panjang khatulistiwa Bumi | 134 milidetik |
| dari Bulan ke Bumi | 1,3 detik |
| dari Matahari ke Bumi (1 SA) | 8,3 menit |
| satu tahun cahaya | 1,0 tahun |
| satu parsec | 3,26 tahun |
| dari bintang terdekat ke Matahari (1,3 parsec) | 4,2 tahun |
| dari galaksi terdekat (Canis Major) ke Bumi | 25.000 tahun |
| menyeberangi Bima Sakti | 100.000 tahun |
| dari Galaksi Andromeda ke Bumi | 2,5 juta tahun |
| dari Bumi ke batas alam semesta teramati | 46,5 miliar tahun |
Laju cahaya atau kecepatan cahaya disimbolkan dengan c adalah sebuah konstanta fisika universal yang penting dalam banyak bidang fisika. Nilai presisinya adalah 299.792.458 meter per detik (kira-kira 300.000 kilometer per detik; 186.000 mil per detik; 671 juta mil per jam), karena panjang meter didefinisikan berdasarkan konstanta ini dan standar internasional waktu.[1] Kelajuan ini merupakan kelajuan maksimum yang dapat dilajui oleh segala bentuk energi, materi, dan informasi dalam alam semesta. Kelajuan ini merupakan kelajuan segala partikel tak bermassa dan medan fisika, termasuk radiasi elektromagnetik dalam vakum. Kelajuan ini pula menurut teori modern adalah kelajuan gravitasi (kelajuan dari gelombang gravitasi). Partikel-partikel maupun gelombang-gelombang ini bergerak pada kelajuan c tanpa tergantung pada sumber gerak maupun kerangka acuan inersial pengamat. Dalam teori relativitas, c saling berkaitan dengan ruang waktu. Konstanta ini muncul pula pada persamaan fisika kesetaraan massa-energi E = mc2.[2]
Kelajuan cahaya yang merambat melalui bahan-bahan transparan seperti gelas ataupun udara lebih lambat dari c. Rasio antara c dengan kelajuan v (kelajuan rambat cahaya dalam suatu materi) disebut sebagai indeks bias n material tersebut (n = c / v). Sebagai contohnya, indeks refraksi gelas umumnya berkisar sekitar 1,5, berarti bahwa cahaya dalam gelas bergerak pada kelajuan c / 1,5 ≈ 200.000 km/s; indeks refraksi udara untuk cahaya tampak adalah sekitar 1,0003, sehingga kelajuan cahaya dalam udara adalah sekitar 299.700 km/s (sekitar 90 km/s lebih lambat daripada c).
Untuk berbagai tujuan praktis, cahaya dan gelombang elektromagnetik lainnya akan tampak untuk menyebar secara seketika, tetapi untuk jarak jauh dan pengukuran yang sangat sensitif, kelajuan terbatasnya memiliki efek yang nyata. Hal inilah yang menimbulkan dilatasi waktu dalam pengamatan. Seperti dalam berkomunikasi dengan wahana antariksa yang jauh, dapat dibutuhkan bermenit-menit sampai berjam-jam agar pesan dari Bumi dapat mencapai pesawat ruang angkasa, atau sebaliknya. Cahaya yang dilihat dari bintang, galaksi dan benda - benda angkasa meninggalkan sumbernya tersebut bertahun-tahun yang lalu, bahkan untuk benda terjauh yang dapat kita lihat dalam alam semesta teramati, apa yang kita lihat di bumi sekarang adalah apa yang terjadi saat ledakan dahsyat terjadi (13,8 miliar tahun yang lalu). Hal ini yang memungkinkan studi tentang sejarah alam semesta dengan melihat objek yang jauh. Kelajuan terbatas cahaya juga membatasi kecepatan maksimum teoretis komputer, karena informasi harus dikirim dalam komputer dari chip ke chip. Kecepatan cahaya dapat digunakan dengan pengukuran waktu terbang untuk mengukur jarak besar dengan presisi tinggi.
Ole Rømer pertama menunjukkan pada 1676 bahwa cahaya berjalan pada kecepatan yang terbatas (bukannya seketika) dengan mempelajari gerakan yang tampak dari bulan Jupiter Io. Pada tahun 1865, James Clerk Maxwell mengusulkan bahwa cahaya adalah gelombang elektromagnetik, dan karena itu bergerak dengan kecepatan c yang muncul dalam teori elektromagnetismenya.[3] Pada tahun 1905, Albert Einstein mendalilkan bahwa laju cahaya sehubungan dengan kerangka inersia independen dari gerakan sumber cahaya,[4] dan menjelajahi konsekuensi postulat dengan menurunkan teori relativitas khusus dan menunjukkan bahwa parameter c memiliki relevansi di luar konteks cahaya dan elektromagnetisme.
Setelah berabad-abad pengukuran semakin tepat, pada tahun 1975 kecepatan cahaya diketahui sebagai 299.792.458 m/s dengan ketidakpastian pengukuran 4 bagian per miliar. Pada tahun 1983, meter didefinisikan kembali dalam Sistem Satuan Internasional (SI) sebagai jarak yang ditempuh oleh cahaya dalam ruang hampa di 1/299.792.458 detik. Akibatnya, nilai numerik dari c dalam meter per detik sekarang tetap persis dengan definisi meter.[5]
Nilai numerik, notasi, dan unit[sunting | sunting sumber]
Laju cahaya dalam ruang hampa biasanya dilambangkan dengan huruf kecil c, untuk "constant" atau bahasa Latin celeritas (yang berarti "kecepatan"). Secara historis, simbol V pernah digunakan sebagai simbol alternatif untuk laju cahaya, yang diperkenalkan oleh James Clerk Maxwell pada tahun 1865. Pada tahun 1856, Wilhelm Eduard Weber dan Rudolf Kohlrausch telah menggunakan c untuk konstanta yang berbeda yang kemudian terbukti sama dengan √2 dikalikan laju cahaya dalam ruang hampa. Pada tahun 1894, Paul Drude mendefinisikan ulang c dengan makna modern. Einstein menggunakan V di makalah aslinya yang berbahasa Jerman tentang relativitas khusus pada tahun 1905, namun pada tahun 1907 ia beralih ke c, yang saat itu telah menjadi simbol standar untuk laju cahaya.[6][7]
Kadang-kadang c digunakan untuk laju gelombang di medium bahan apapun, dan c0 untuk laju cahaya dalam ruang hampa.[8] Notasi subscript ini, yang didukung dalam literatur SI resmi,[5] memiliki bentuk yang sama sebagai konstanta terkait lainnya: yaitu, μ0 untuk permeabilitas vakum atau konstanta magnetik, ε0 untuk permitivitas vakum atau konstanta listrik, dan Z0 untuk impedansi ruang hampa. Artikel ini menggunakan c eksklusif untuk kecepatan cahaya dalam ruang hampa.
Sejak tahun 1983, meter telah didefinisikan dalam Sistem Satuan Internasional (SI) sebagai jarak perjalanan cahaya dalam ruang hampa dalam 1⁄299.792.458 detik. Definisi ini menetapkan laju cahaya dalam ruang hampa di persis 299.792.458 m/s.[9][10][11] Sebagai sebuah konstanta fisika berdimensi, nilai numerik dari c berbeda untuk sistem unit yang berbeda.[catatan 3] Dalam cabang fisika di mana c sering muncul, seperti dalam relativitas, biasa digunakan sistem pengukuran satuan natural atau sistem satuan tergeometrisasi dengan c = 1.[13][14] Menggunakan unit-unit ini, c tidak muncul secara eksplisit karena perkalian atau pembagian dengan 1 tidak memengaruhi hasil.
Peran fundamental dalam fisika[sunting | sunting sumber]
Kelajuan dari gelombang cahaya yang merambat dalam ruang hampa tidak bergantung pada gerakan sumber gelombang ataupun kerangka acuan inersial pengamat.[catatan 4] Invariansi dari kecepatan cahaya ini didalilkan oleh Einstein pada tahun 1905,[4] setelah termotivasi oleh teori elektromagnetisme Maxwell dan kurangnya bukti keberadaan eter yang sebelumnya diduga sebagai medium cahaya;[15] invariansi tersebut sejak saat itu telah secara konsisten dikonfirmasi oleh banyak percobaan. Verifikasi secara eksperimental bahwa laju cahaya tidak bergantung pada kerangka acuan hanya bisa dilakukan untuk laju cahaya dua arah (misalnya, dari sumber ke cermin dan kembali lagi), karena tidak mungkin untuk mengukur laju cahaya satu arah (misalnya, dari sumber ke detektor yang jauh) tanpa beberapa konvensi mengenai bagaimana jam pada sumber dan pada detektor harus disinkronkan. Namun, dengan mengadopsi sinkronisasi Einstein untuk jam, kecepatan satu arah cahaya menjadi sama dengan kecepatan dua arah cahaya secara definisi.[16][17] Teori relativitas khusus mengeksplorasi konsekuensi dari invariansi c dengan asumsi bahwa hukum fisika adalah sama dalam semua kerangka acuan inersial.[18][19] Salah satu konsekuensinya adalah semua gelombang dan partikel tak bermassa, termasuk cahaya, harus berjalan dengan kelajuan c dalam ruang hampa.
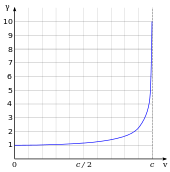
Relativitas khusus memiliki banyak implikasi yang berlawanan dengan intuisi dan telah diverifikasi lewat berbagai percobaan.[20] Ini termasuk kesetaraan massa dan energi (E = mc2), kontraksi panjang (benda bergerak menjadi lebih pendek),[catatan 5] dan dilatasi waktu (jam bergerak berjalan lebih lambat). Faktor γ yang menentukan besar kontraksi panjang dan dilatasi waktu dikenal sebagai faktor Lorentz dan diberikan oleh γ = (1 − v2/c2)−1/2, di mana v adalah kelajuan benda. Selisih antara γ dengan 1 dapat diabaikan untuk kelajuan yang jauh lebih lambat dari c, seperti kebanyakan kecepatan sehari-hari—di mana relativitas khusus didekati oleh relativitas Galileo—tetapi meningkat pada kecepatan relativistik dan menyimpang hingga tak terbatas ketika v mendekati c.
Hasil dari relativitas khusus dapat diringkas dengan memperlakukan ruang dan waktu sebagai struktur terpadu yang dikenal sebagai ruang waktu (dengan c mengaitkan satuan ruang dan waktu), dan mengharuskan teori fisika memenuhi suatu simetri khusus yang disebut invariansi Lorentz, yaitu formulasi matematis yang berisi parameter c.[23] Invariansi Lorentz diasumsikan berlaku oleh hampir seluruh teori-teori fisika modern, seperti elektrodinamika kuantum, kromodinamika kuantum, Model Standar fisika partikel, dan relativitas umum. Dengan demikian, parameter c ada di mana-mana dalam fisika modern, muncul dalam banyak konteks yang tidak berhubungan dengan cahaya. Misalnya, relativitas umum memprediksi bahwa c juga merupakan kelajuan gravitasi dan gelombang gravitasi.[24][25] Pada kerangka acuan non-inersial (ruang waktu yang dilengkungkan oleh gravitasi atau kerangka acuan dipercepat), laju lokal cahaya adalah konstan dan sama dengan c, tetapi laju cahaya di sepanjang lintasan panjang yang terbatas dapat berbeda dari c, tergantung pada bagaimana jarak dan waktu ditentukan.[26]
Secara umum diasumsikan bahwa konstanta fundamental seperti c memiliki nilai yang sama di seluruh ruang waktu, yang berarti bahwa mereka tidak bergantung pada lokasi dan tidak berubah seiring waktu. Namun, telah diusulkan dalam berbagai teori bahwa laju cahaya mungkin telah berubah dari waktu ke waktu.[27][28] Tidak ada bukti konklusif untuk perubahan tersebut yang telah ditemukan, tetapi hal itu tetap menjadi subjek penelitian yang sedang berlangsung.[29][30]
Umumnya juga diasumsikan bahwa kecepatan cahaya bersifat isotropik, yang berarti bahwa ia memiliki nilai yang sama tidak bergantung arah di mana itu diukur. Pengamatan dari emisi dari tingkat energi nuklir sebagai fungsi orientasi inti atom yang memancarkan emisi dalam medan magnet (lihat percobaan Hughes-Drever), dan resonator optik berputar (lihat percobaan resonator) telah memberi batas ketat pada kemungkinan isotropi dua arah.[31][32]
Batas atas kelajuan[sunting | sunting sumber]
Menurut relativitas khusus, energi dari suatu objek dengan massa diam m dan kelajuan v diberikan oleh γmc2, di mana γ adalah faktor Lorentz yang didefinisikan di atas. Ketika v adalah nol, γ sama dengan satu, sehingga menimbulkan rumus terkenal E = mc2 untuk kesetaraan massa-energi. Faktor γ mendekati tak terhingga ketika v mendekati c, jadi diperlukan energi dengan jumlah tak terbatas untuk mempercepat objek bermassa ke laju cahaya. Laju cahaya adalah batas atas untuk kelajuan benda dengan massa diam positif, dan foton individu tidak dapat melakukan perjalanan lebih cepat dari laju cahaya.[33][34] Ini telah dibuktikan secara eksperimental dalam berbagai uji energi dan momentum relativistik.[35]

Secara lebih umum, tidak mungkin informasi atau energi bisa melakukan perjalanan lebih cepat dari c. Salah satu argumen untuk ini mengikuti dari implikasi tidak intuitif relativitas khusus yang dikenal sebagai relativitas simultanitas. Jika jarak spasial antara dua peristiwa A dan B lebih besar dari interval waktu antara mereka dikalikan dengan c maka ada kerangka acuan di mana A mendahului B, yang lain di mana B mendahului A, dan yang lain di mana mereka terjadi bersamaan. Akibatnya, jika sesuatu bepergian lebih cepat dari c relatif terhadap sebuah kerangka acuan inersial, maka benda tersebut akan berjalan mundur dalam waktu relatif terhadap bingkai lain, dan kausalitas akan dilanggar.[catatan 6][37] Dalam kerangka acuan ini, sebuah "akibat" bisa diamati sebelum "penyebab"-nya. Pelanggaran kausalitas seperti itu tidak pernah direkam,[17] dan akan menyebabkan paradoks seperti antitelepon takion.[38]
Pengamatan dan eksperimen lebih-cepat-dari-cahaya[sunting | sunting sumber]
Ada situasi di mana mungkin tampak bahwa materi, energi, atau informasi bergerak dengan laju lebih besar dari c, tetapi sebenarnya tidak. Misalnya, seperti yang dibahas dalam bagian perambatan cahaya di sebuah medium di bawah, banyak kecepatan gelombang dapat melebihi c. Misalnya, kecepatan fase sinar-X melalui sebagian besar kaca secara rutin dapat melebihi c,[39] tetapi kecepatan fase tidak menentukan kecepatan di mana gelombang menyampaikan informasi.[40]
Jika sinar laser menyapu cepat sebuah objek yang jauh, titik cahayanya dapat bergerak lebih cepat dari c, meskipun gerakan awal titik tersebut tertunda karena waktu yang dibutuhkan cahaya untuk sampai ke objek yang jauh dengan kelajuan c. Namun, satu-satunya entitas fisik yang bergerak adalah laser dan cahaya yang dipancarkan, yang bergerak dengan kelajuan c dari laser ke berbagai posisi tempat titik terlihat. Demikian pula, bayangan yang diproyeksikan ke sebuah objek yang jauh dapat dibuat untuk bergerak lebih cepat dari c, setelah penundaan dalam waktu.[41] Dalam kedua kasus tersebut tidak ada materi, energi, atau informasi yang bergerak lebih cepat dari cahaya.[42]
Tingkat perubahan dalam jarak antara dua objek dalam suatu kerangka acuan terhadap yang keduanya bergerak (kelajuan penutupan mereka) mungkin memiliki nilai lebih dari c. Namun, ini tidak mewakili kecepatan dari setiap objek tunggal yang diukur dalam kerangka inersia tunggal.[42]
Efek kuantum tertentu tampaknya dikirimkan secara instan dan lebih cepat dari c, seperti dalam paradoks EPR. Sebuah contoh melibatkan keadaan kuantum dari dua partikel yang dapat terjerat. Sampai salah satu partikel diamati, mereka berada dalam superposisi dari dua keadaan kuantum. Jika partikel dipisahkan dan keadaan kuantum satu partikel diamati, keadaan kuantum partikel lain ditentukan seketika (lebih cepat dari cahaya yang pergi dari satu partikel ke yang lain). Namun, tidak mungkin untuk mengontrol keadaan kuantum apa yang partikel pertama akan ambil ketika diamati, sehingga informasi tidak dapat dikirimkan dengan cara ini.[42][43]
Efek kuantum lain yang memprediksi terjadinya kelajuan lebih cepat dari cahaya disebut efek Hartman; dalam kondisi tertentu waktu yang diperlukan untuk sebuah partikel virtual untuk menerowong melalui penghalang adalah konstan, terlepas dari ketebalan penghalang.[44][45] Hal ini dapat mengakibatkan partikel virtual melintasi jarak yang besar lebih cepat dari cahaya. Namun, tidak ada informasi yang dapat dikirim dengan efek ini.[46]
Gerak superluminal terlihat di objek astronomi tertentu,[47] seperti jet relativistik galaksi radio dan kuasar. Namun, jet ini tidak bergerak dengan kelajuan lebih dari laju cahaya: gerakan superluminal yang tampak adalah efek proyeksi yang disebabkan oleh benda yang bergerak mendekati laju cahaya dan mendekati Bumi pada sudut kecil dengan garis pandang: karena cahaya yang dipancarkan ketika jet itu lebih jauh membutuhkan waktu lebih lama untuk mencapai Bumi, waktu antara dua pengamatan berturut-turut sesuai dengan waktu yang lebih lama antara saat sinar-sinar cahaya dipancarkan.[48]
Dalam model alam semesta yang mengembang, semakin jauh galaksi dari satu sama lain, semakin cepat mereka menjauh. Kemunduran ini bukan karena gerakan melalui ruang, melainkan karena perluasan ruang itu sendiri.[42] Misalnya, galaksi yang jauh dari Bumi tampaknya bergerak menjauh dari Bumi dengan kelajuan sebanding dengan jarak mereka. Melampaui batas yang disebut bola Hubble, tingkat di mana jarak mereka dari Bumi meningkat menjadi lebih besar dari laju cahaya.[49]
Perambatan cahaya[sunting | sunting sumber]
Dalam fisika klasik, cahaya dideskripsikan sebagai jenis gelombang elektromagnetik. Perilaku klasik medan elektromagnetik dijelaskan oleh persamaan Maxwell, yang memprediksi bahwa kelajuan c di mana gelombang elektromagnetik (seperti cahaya) menyebar melalui vakum terkait dengan konstanta listrik ε0 dan konstanta magnetik μ0 dengan persamaan [50]
Dalam fisika kuantum modern, medan elektromagnetik dijelaskan oleh teori elektrodinamika kuantum (quantum electrodynamics, QED). Dalam teori ini, cahaya dideskripsikan oleh eksitasi mendasar (atau kuanta) dari medan elektromagnetik, yang disebut foton. Dalam QED, foton adalah partikel tak bermassa dan dengan demikian, menurut relativitas khusus, mereka melakukan perjalanan dengan laju cahaya dalam ruang hampa.
Ekstensi dari QED di mana foton memiliki massa telah dipertimbangkan. Dalam teori semacam itu, kecepatannya akan tergantung pada frekuensi, dan kelajuan invarian c dari relativitas khusus maka akan menjadi batas atas laju cahaya dalam ruang hampa.[26] Variasi laju cahaya yang disebabkan oleh frekuensi belum pernah diamati dalam pengujian yang ketat,[51][52][53] menempatkan batas yang ketat pada massa foton. Batas diperoleh tergantung pada model yang digunakan: jika foton masif dijelaskan menggunakan teori Proca,[54] batas atas eksperimental untuk massa adalah sekitar 10−57 gram;[55] jika massa foton dihasilkan oleh mekanisme Higgs, batas atas eksperimental kurang tajam, m ≤ 10−14 eV/c2 [54] (kira-kira 2 × 10−47 g).
Alasan lain untuk kecepatan cahaya bervariasi sesuai frekuensi adalah kegagalan relativitas khusus untuk berlaku pada skala yang kecil, seperti yang diperkirakan oleh beberapa teori yang diusulkan dari gravitasi kuantum. Pada tahun 2009, pengamatan spektrum semburan sinar gamma GRB 090510 tidak menemukan perbedaan dalam kecepatan foton dengan energi yang berbeda, membenarkan bahwa invariansi Lorentz terverifikasi setidaknya sampai ke skala panjang Planck (lP = √ħG/c3 ≈ 1,6163×10−35 m) dibagi dengan 1,2.[56]
Di sebuah medium[sunting | sunting sumber]
Dalam sebuah medium, cahaya biasanya tidak bergerak pada laju yang sama dengan c; berbagai jenis gelombang cahaya akan melakukan perjalanan pada kelajuan yang berbeda. Kelajuan di mana puncak-puncak individu dan palung dari gelombang bidang (gelombang mengisi seluruh ruang, dengan hanya satu frekuensi) merambat disebut kecepatan fase vp. Sinyal fisik dengan batas terbatas (pulsa cahaya) bergerak pada kelajuan yang berbeda. Bagian terbesar dari pulsa berjalan dengan kecepatan kelompok vg, dan bagian paling awal berjalan dengan kecepatan depan vf.
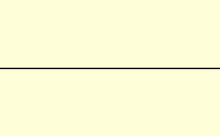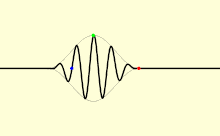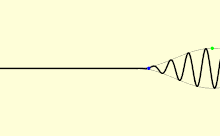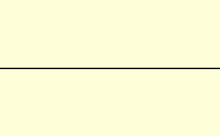
Kecepatan fase penting dalam menentukan bagaimana gelombang cahaya bergerak melalui materi atau dari satu materi ke materi yang lain. Hal ini sering dilambangkan menggunakan indeks bias. Indeks bias dari suatu materi didefinisikan sebagai rasio c terhadap kecepatan fase vp dalam materi: indeks bias lebih besar menunjukkan kelajuan yang lebih rendah. Indeks bias dari suatu materi mungkin tergantung pada frekuensi, intensitas, polarisasi, atau arah perambatan cahaya; tetapi dalam banyak kasus, indeks bias dapat diperlakukan sebagai konstanta yang hanya bergantung pada bahan. Indeks bias udara adalah sekitar 1,0003.[57] Media yang lebih padat, seperti air,[58] kaca,[59] dan intan,[60] memiliki indeks bias masing-masing sekitar 1,3, 1,5 dan 2,4 untuk cahaya tampak. Dalam bahan eksotis seperti kondensat Bose–Einstein di dekat nol mutlak, laju efektif cahaya mungkin hanya beberapa meter per detik. Namun, ini merupakan penundaan yang disebabkan penyerapan dan pemancaran kembali antara atom-atom, begitu pula kelajuan cahaya yang lebih lambat dari c dalam zat materi lainnya. Sebagai contoh ekstrem dari "perlambatan" cahaya dalam materi, dua tim independen dari fisikawan mengaku menjadikan cahaya "berhenti sepenuhnya" dengan melewatkannya melalui kondensat Bose–Einstein dari unsur rubidium, satu tim di Universitas Harvard dan Rowland Institute for Science di Cambridge, Mass., dan yang lainnya di Harvard-Smithsonian Center for Astrophysics, juga di Cambridge. Namun, deskripsi populer cahaya "berhenti" dalam percobaan ini hanya mengacu pada cahaya yang disimpan dalam keadaan tereksitasi dari atom, kemudian kembali dipancarkan pada waktu kemudian, karena dirangsang oleh pulsa laser kedua. Selama "berhenti," hal itu tidak lagi menjadi cahaya. Jenis perilaku ini umumnya benar secara mikroskopis di semua media transparan yang "memperlambat" laju cahaya.[61]
Dalam bahan transparan, indeks bias umumnya lebih besar dari 1, berarti bahwa kecepatan fase kurang dari c. Dalam bahan lain, adalah mungkin untuk indeks bias menjadi lebih kecil dari 1 untuk beberapa frekuensi; di beberapa bahan eksotis bahkan dimungkinkan untuk indeks bias menjadi negatif.[62] Persyaratan bahwa kausalitas tidak dilanggar menyiratkan bahwa bagian real dan imajiner dari konstanta dielektrik dari bahan apapun, sesuai masing-masing dengan indeks bias dan dengan koefisien atenuasi, dihubungkan oleh hubungan Kramer–Kronig.[63] Dalam bahasa praktis, ini berarti bahwa dalam bahan dengan indeks bias kurang dari 1, penyerapan gelombang terjadi sangat cepat sehingga tidak ada sinyal yang dapat dikirim lebih cepat dari c.
Sebuah pulsa dengan kecepatan kelompok dan fase yang berbeda (yang terjadi jika kecepatan fase tidak sama untuk semua frekuensi pulsa) menyebar dari waktu ke waktu, sebuah proses yang dikenal sebagai dispersi. Bahan-bahan tertentu memiliki kecepatan kelompok yang sangat rendah (atau bahkan nol) untuk gelombang cahaya, fenomena yang disebut cahaya lambat, yang telah dikonfirmasi di berbagai eksperimen.[64][65][66][67] Sebaliknya, kecepatan kelompok melebihi c, juga telah ditunjukkan dalam percobaan.[68] Bahkan mungkin untuk kecepatan kelompok menjadi tak terhingga atau negatif, dengan pulsa bepergian secara instan atau mundur dalam waktu.[69]
Tak satu pun dari pilihan ini, bagaimanapun, memungkinkan informasi dikirim lebih cepat dari c. Tidak mungkin untuk mengirimkan informasi dengan pulsa cahaya lebih cepat dari kecepatan bagian awal dari pulsa (kecepatan depan). Bisa ditunjukkan bahwa kecepatan depan (di bawah asumsi tertentu) selalu sama dengan c.[69]
Mungkin saja sebuah partikel melakukan perjalanan melalui media lebih cepat daripada kecepatan fase cahaya dalam medium (tetapi masih lebih lambat dari c). Ketika partikel bermuatan melakukan itu dalam bahan dielektrik, ekuivalen elektromagnetik dari gelombang kejut, dikenal sebagai radiasi Cherenkov, dipancarkan.[70]
Efek praktis dari keterbatasan[sunting | sunting sumber]
Laju cahaya relevan dengan komunikasi: waktu tunda pulang-pergi dan satu arah pasti bernilai lebih besar dari nol. Hal ini berlaku dari skala kecil sampai astronomi. Di sisi lain, beberapa teknik bergantung pada laju terbatas cahaya, misalnya dalam pengukuran jarak.
Skala kecil[sunting | sunting sumber]
Dalam superkomputer, kecepatan cahaya memberlakukan batas pada seberapa cepat data dapat dikirim antara prosesor. Jika prosesor beroperasi pada 1 gigahertz, sinyal hanya dapat melakukan perjalanan maksimum sekitar 30 cm dalam satu siklus. Prosesor karena itu harus ditempatkan dekat satu sama lain untuk meminimalkan latensi komunikasi; ini dapat menyebabkan kesulitan dengan pendingin. Jika frekuensi jam terus meningkat, laju cahaya pada akhirnya akan menjadi faktor pembatas untuk desain internal cip tunggal.[71]
Jarak yang besar di Bumi[sunting | sunting sumber]
Karena lingkar ekuator Bumi memiliki panjang sekitar 40.075 km dan c bernilai sekitar 300.000 km/s, waktu tersingkat teoretis yang dibutuhkan sepotong informasi untuk melakukan perjalanan melintasi setengah keliling permukaan Bumi adalah sekitar 67 milidetik. Ketika cahaya berjalan di seluruh dunia dalam serat optik, waktu transit yang sebenarnya lebih panjang, sebagian karena kecepatan cahaya lebih lambat sekitar 35% dalam serat optik, tergantung pada indeks bias n-nya.[72] Selanjutnya, garis lurus jarang terjadi dalam situasi komunikasi global, dan penundaan terjadi ketika sinyal melewati sebuah switch elektronik atau regenerator sinyal.[73]
Penerbangan ruang angkasa dan astronomi[sunting | sunting sumber]

Demikian pula, komunikasi antara Bumi dan pesawat ruang angkasa tidak seketika. Ada penundaan singkat dari sumber ke penerima, yang menjadi lebih terlihat ketika jarak meningkat. Penundaan ini signifikan bagi komunikasi antara kontrol tanah dan Apollo 8 ketika menjadi pesawat ruang angkasa berawak pertama yang mengorbit Bulan: untuk setiap pertanyaan, stasiun kontrol tanah harus menunggu setidaknya tiga detik untuk jawaban tiba.[74] Penundaan komunikasi antara Bumi dan Mars bisa bervariasi antara lima dan dua puluh menit tergantung pada posisi relatif dari kedua planet tersebut. Sebagai konsekuensi dari ini, jika robot di permukaan Mars menghadapi masalah, pengendali manusia tidak akan menyadari hal itu sampai setidaknya lima menit kemudian, dan mungkin sampai dua puluh menit kemudian; kemudian akan membutuhkan lima sampai dua puluh menit bagi petunjuk untuk melakukan perjalanan dari Bumi ke Mars.
NASA harus menunggu beberapa jam untuk informasi dari pesawat ruang angkasa yang mengorbit Jupiter, dan jika perlu untuk memperbaiki kesalahan navigasi, perbaikan tidak akan sampai pada pesawat ruang angkasa untuk jumlah waktu yang sama, menciptakan risiko koreksi tidak tiba pada waktunya.
Menerima cahaya dan sinyal dari sumber astronomi jauh bahkan dapat memakan waktu lebih lama. Sebagai contoh, dibutuhkan 13 miliar (13×109) tahun bagi cahaya untuk melakukan perjalanan ke Bumi dari galaksi jauh yang dilihat dalam gambar Hubble Ultra Deep Field.[75][76] Foto-foto itu, yang diambil hari ini, menangkap gambar galaksi sebagaimana mereka tampak 13 miliar tahun yang lalu, ketika alam semesta berusia kurang dari satu miliar tahun.[75] Fakta bahwa objek yang lebih jauh tampak lebih muda, karena laju cahaya yang terbatas, memungkinkan para astronom untuk menyimpulkan evolusi bintang, galaksi, dan alam semesta itu sendiri.
Jarak astronomi kadang-kadang dinyatakan dalam tahun cahaya, terutama dalam publikasi sains populer dan media.[77] Satu tahun cahaya adalah jarak yang ditempuh cahaya dalam satu tahun, sekitar 9461 miliar kilometer, 5879 miliar mil, atau 0,3066 parsec. Dalam angka bulat, satu tahun cahaya adalah hampir 10 triliun kilometer atau hampir 6 triliun mil. Proxima Centauri, bintang terdekat dengan Bumi setelah Matahari, sekitar 4,2 tahun cahaya.[78]
Pengukuran jarak[sunting | sunting sumber]
Sistem radar mengukur jarak ke target dengan waktu yang dibutuhkan pulsa gelombang radio untuk kembali ke antena radar setelah dipantulkan oleh target: jarak ke target adalah setengah waktu transit pulang-pergi yang dikalikan dengan laju cahaya. Sebuah penerima Global Positioning System (GPS) mengukur jarak ke satelit GPS berdasarkan berapa lama waktu yang dibutuhkan untuk sinyal radio tiba dari setiap satelit, dan dari jarak ini menghitung posisi penerima. Karena cahaya bergerak sekitar 300.000 kilometer (186.000 mi) dalam satu detik, pengukuran pecahan kecil dari detik harus sangat tepat. Lunar Laser Ranging Experiment, astronomi radar dan Deep Space Network menentukan jarak ke Bulan,[79] planet[80] dan pesawat ruang angkasa,[81] secara berurutan, dengan mengukur waktu transit pulang-pergi.
Perdagangan frekuensi tinggi[sunting | sunting sumber]
Laju cahaya telah menjadi penting dalam perdagangan frekuensi tinggi, di mana para pedagang berusaha untuk mendapatkan keuntungan menit dengan memberikan perdagangan mereka untuk pertukaran pecahan detik lebih dulu dari pedagang lainnya. Misalnya, pedagang telah beralih ke komunikasi gelombang mikro antara hub perdagangan, karena keuntungan gelombang mikro bepergian di dekat laju cahaya di udara, lebih dari sinyal serat optik yang bepergian 30-40% lebih lambat dari laju cahaya melalui kaca.[82]
Pengukuran[sunting | sunting sumber]
Ada berbagai cara untuk menentukan nilai c. Salah satu cara adalah dengan mengukur laju yang sebenarnya di mana gelombang cahaya merambat, yang dapat dilakukan dengan berbagai setup astronomi dan berbasis-bumi. Namun, juga mungkin untuk menentukan c dari hukum fisika lainnya di mana ia muncul, misalnya, dengan menentukan nilai-nilai konstanta elektromagnetik ε0 dan μ0 dan menggunakan hubungan mereka dengan c. Secara historis, hasil yang paling akurat telah diperoleh dengan secara terpisah menentukan frekuensi dan panjang gelombang sinar, dengan hasil kali mereka menyamai c.
Pada tahun 1983 meter didefinisikan sebagai "panjang jalan yang ditempuh oleh cahaya dalam ruang hampa selama selang waktu dari ⅟299.792.458 detik",[83] menetapkan nilai laju cahaya di 299.792.458 m/s secara definisi, seperti yang dijelaskan di bawah ini. Akibatnya, pengukuran akurat dari kecepatan cahaya menghasilkan realisasi akurat dari meter, bukannya nilai yang akurat dari c.
Pengukuran astronomis[sunting | sunting sumber]

Luar angkasa adalah tempat yang nyaman untuk mengukur laju cahaya karena skalanya yang besar dan vakumnya yang hampir sempurna. Biasanya, seseorang mengukur waktu yang dibutuhkan untuk cahaya untuk melintasi jarak referensi dalam tata surya, seperti jari-jari orbit bumi. Secara historis, pengukuran tersebut dapat dibuat cukup akurat, dibandingkan dengan seberapa akurat panjang jarak referensi dikenal di unit berbasis Bumi. Sudah menjadi kebiasaan untuk mengekspresikan hasilnya dalam satuan astronomi (SA) per hari.
Ole Christensen Rømer menggunakan pengukuran astronomis untuk membuat estimasi kuantitatif pertama dari laju cahaya.[84][85] Ketika diukur dari Bumi, periode bulan yang mengorbit sebuah planet lebih pendek saat Bumi mendekati planet tersebut daripada ketika bumi sedang menjauhinya. Jarak yang ditempuh oleh cahaya dari planet (atau bulannya) ke Bumi lebih pendek saat Bumi berada pada titik di orbitnya yang paling dekat dengan planet dibandingkan saat Bumi berada pada titik terjauh di orbitnya, perbedaan jarak adalah diameter orbit Bumi mengelilingi Matahari. Perubahan yang diamati dalam periode orbit bulan disebabkan oleh perbedaan waktu yang dibutuhkan cahaya untuk melintasi jarak yang lebih pendek atau lebih panjang. Rømer mengamati efek ini untuk bulan terdalam Jupiter Io dan menyimpulkan bahwa cahaya memerlukan 22 menit untuk menyeberangi diameter orbit bumi.
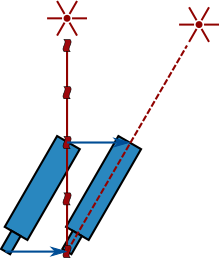
Cara lain adalah dengan menggunakan aberasi cahaya, ditemukan dan dijelaskan oleh James Bradley pada abad ke-18.[86] Efek ini dihasilkan dari penjumlahan vektor dari laju cahaya yang datang dari sumber yang jauh (seperti bintang) dan kecepatan pengamat (lihat diagram di sebelah kanan), sehingga seorang pengamat yang bergerak melihat cahaya yang datang dari arah yang sedikit berbeda dan akibatnya melihat sumber di posisi yang bergeser dari posisi semula. Karena arah kecepatan bumi berubah terus-menerus ketika Bumi mengorbit Matahari, efek ini menyebabkan posisi bintang tampak bergerak. Dari perbedaan sudut dalam posisi bintang (maksimal 20,5 detik busur)[87] adalah mungkin untuk mengekspresikan laju cahaya dalam hal kecepatan Bumi mengelilingi matahari, yang dengan panjang selang waktu setahun dapat dikonversi ke waktu yang dibutuhkan untuk perjalanan dari Matahari ke Bumi. Pada 1729, Bradley menggunakan metode ini untuk mendapatkan bahwa cahaya melakukan perjalanan 10.210 kali lebih cepat dari Bumi di orbitnya (angka modern 10.066 kali lebih cepat) atau, secara setara, bahwa cahaya membutuhkan 8 menit 12 detik untuk melakukan perjalanan dari Matahari ke Bumi.[86]
Satuan astronomi[sunting | sunting sumber]
Satuan astronomi (SA) adalah kira-kira jarak rata-rata antara Bumi dan Matahari. SA didefinisikan kembali pada tahun 2012 sebagai persis 149.597.870.700 m.[88][89] Sebelumnya SA tidak didasarkan pada Sistem Satuan Internasional tetapi dalam hal gaya gravitasi yang diberikan oleh Matahari dalam mekanika klasik.[catatan 7] Definisi saat ini menggunakan nilai yang direkomendasikan dalam meter untuk definisi satuan astronomi sebelumnya, yang ditentukan oleh pengukuran.[88] Redefinisi ini analog dengan meter, dan juga memiliki efek menetapkan laju cahaya ke nilai yang tepat dalam satuan astronomi per detik (melalui laju cahaya yang tepat dalam meter per detik).
Sebelumnya, kebalikan dari c dinyatakan dalam detik per satuan astronomi diukur dengan membandingkan waktu untuk sinyal radio untuk mencapai pesawat ruang angkasa yang berbeda di Tata Surya, dengan posisi mereka dihitung dari efek gravitasi Matahari dan berbagai planet. Dengan menggabungkan banyak pengukuran tersebut, nilai terbaik untuk waktu cahaya per satuan jarak dapat diperoleh. Misalnya, pada tahun 2009, estimasi terbaik, yang disetujui oleh International Astronomical Union (IAU), adalah:[91][92]
- Waktu cahaya untuk satuan jarak: 499,004783836(10) s
- c = 0,00200398880410(4) SA/s = 173,144632674(3) SA/hari.
Ketidakpastian relatif dalam pengukuran ini adalah 0,02 bagian per miliar (2×10−11), setara dengan ketidakpastian dalam pengukuran panjang berbasis Bumi dengan interferometri.[93] Karena meter didefinisikan sebagai jarak tempuh cahaya dalam interval waktu tertentu, pengukuran waktu cahaya dalam hal definisi satuan astronomi yang sebelumnya juga dapat diartikan sebagai mengukur panjang satu SA (definisi lama) dalam meter.[catatan 8]
Teknik waktu terbang[sunting | sunting sumber]


Salah satu metode pengukuran laju cahaya adalah mengukur waktu yang dibutuhkan oleh cahaya untuk melakukan perjalanan ke cermin di jarak yang diketahui dan kembali. Ini adalah prinsip yang bekerja pada aparatus Fizeau–Foucault yang dikembangkan oleh Hippolyte Fizeau dan Léon Foucault.
Pengaturan seperti yang digunakan oleh Fizeau terdiri dari seberkas cahaya diarahkan pada cermin 8 kilometer (5 mi) jauhnya. Dalam perjalanan dari sumber ke cermin, berkas cahaya melewati roda bergigi yang berputar. Pada tingkat rotasi tertentu, berkas cahaya melewati satu celah di jalan keluar dan celah lain dalam perjalanan kembali, tetapi pada tingkat sedikit lebih tinggi atau lebih rendah, berkas cahaya menghantam gigi dan tidak melewati roda. Mengetahui jarak antara roda dan cermin, jumlah gigi pada roda, dan tingkat rotasi, laju cahaya dapat dihitung.[94]
Metode Foucault menggantikan roda bergigi dengan cermin berputar. Karena cermin terus berputar sementara cahaya berjalan ke cermin jauh dan kembali, cahaya dipantulkan dari cermin berputar pada sudut yang berbeda pada jalan keluar daripada di jalan kembali. Dari perbedaan sudut ini, kelajuan rotasi dan jarak ke cermin jauh yang diketahui laju cahaya dapat dihitung.[95]
Saat ini, menggunakan osiloskop dengan resolusi waktu kurang dari satu nanodetik, laju cahaya dapat langsung diukur dengan waktu penundaan pulsa cahaya dari laser atau LED dipantulkan dari cermin. Metode ini kurang tepat (dengan kesalahan berorde 1%) daripada teknik modern lainnya, tetapi kadang-kadang digunakan sebagai percobaan laboratorium di kelas fisika perguruan tinggi.[96][97][98]
Konstanta elektromagnetik[sunting | sunting sumber]
Opsi untuk menurunkan c yang tidak secara langsung tergantung pada pengukuran perambatan gelombang elektromagnetik adalah dengan menggunakan hubungan antara c dan permitivitas vakum ε0 dan permeabilitas vakum μ0 didirikan oleh teori Maxwell: c2 = 1/(ε0μ0). Permitivitas vakum dapat ditentukan dengan mengukur kapasitansi dan dimensi kapasitor, sedangkan nilai permeabilitas vakum adalah tetap di persis 4π×10−7 H⋅m−1 melalui definisi ampere. Rosa dan Dorsey menggunakan metode ini pada tahun 1907 untuk menemukan nilai 299.710±22 km/s.[99][100]
Resonansi rongga[sunting | sunting sumber]

Cara lain untuk mengukur laju cahaya adalah dengan secara terpisah mengukur frekuensi f dan panjang gelombang λ dari gelombang elektromagnetik dalam vakum. Nilai c kemudian didapatkan dengan hubungan c = fλ. Salah satu pilihannya adalah mengukur frekuensi resonansi dari sebuah resonator rongga. Jika dimensi rongga resonansi juga diketahui, ini dapat digunakan untuk menentukan panjang gelombang dari gelombang itu. Pada tahun 1946, Louis Essen dan A.C. Gordon-Smith menentukan frekuensi dari sebuah macam mode normal gelombang mikro dari rongga gelombang mikro dengan dimensi yang diketahui dengan teliti. Dimensi ditentukan dengan akurasi sekitar ±0,8 μm menggunakan alat ukur yang dikalibrasi dengan interferometri.[99] Karena panjang gelombang mode diketahui dari geometri rongga dan dari teori elektromagnetik, pengetahuan dari frekuensi yang terkait memungkinkan penghitungan panjang gelombang.[99][101]
Hasil Essen-Gordon-Smith, 299.792±9 km/s, secara substansial lebih tepat daripada yang ditemukan dengan teknik optik.[99] Pada tahun 1950, pengukuran ulang oleh Essen menetapkan hasil 299.792,5±3,0 km/s.[102]
Sebuah demonstrasi rumah tangga dari teknik ini adalah mungkin, menggunakan oven gelombang mikro dan makanan seperti marshmallow atau margarin: jika meja putar diambil sehingga makanan tidak bergerak, makanan akan termasak paling cepat di perut gelombang (titik-titik di mana amplitudo gelombang adalah yang terbesar), di mana ia akan mulai mencair. Jarak antara dua titik tersebut adalah setengah panjang gelombang dari gelombang mikro; dengan mengukur jarak ini dan mengalikan panjang gelombang dengan frekuensi gelombang mikro (biasanya ditampilkan di bagian belakang oven, biasanya 2450 MHz), nilai c dapat dihitung, "biasanya dengan kesalahan kurang dari 5%".[103][104]
Interferometri[sunting | sunting sumber]

Interferometri adalah metode lain untuk menemukan panjang gelombang radiasi elektromagnetik untuk menentukan laju cahaya.[105] Seberkas cahaya koheren (misalnya dari laser), dengan frekuensi yang diketahui (f), dibagi untuk mengikuti dua jalur dan kemudian digabungkan. Dengan menyesuaikan panjang jalur sambil mengamati pola interferensi dan dengan hati-hati mengukur perubahan panjang jalur, panjang gelombang cahaya (λ) dapat ditentukan. Laju cahaya kemudian dihitung menggunakan persamaan c = λf.
Sebelum munculnya teknologi laser, sumber radio yang koheren digunakan untuk pengukuran interferometri dari laju cahaya.[106] Namun penentuan interferometri dari panjang gelombang semakin kurang tepat seiring bertambahnya panjang gelombang sehingga ketepatan percobaan terbatasi oleh panjang gelombang radio yang panjang (~0,4 cm). Presisi dapat ditingkatkan menggunakan cahaya dengan panjang gelombang yang lebih pendek, tetapi kemudian menjadi sulit untuk langsung mengukur frekuensi cahaya. Salah satu cara mengatasi masalah ini adalah mulai dengan sinyal frekuensi rendah dari frekuensi yang dapat diukur dengan tepat, dan dari sinyal ini semakin mensintesis sinyal frekuensi yang lebih tinggi yang frekuensinya dapat dihubungkan dengan sinyal asli. Sebuah laser kemudian dapat dikunci frekuensinya, dan panjang gelombang dapat ditentukan dengan interferometri.[107] Teknik ini berasal dari sebuah kelompok di National Bureau of Standards (NBS) (yang kemudian menjadi NIST). Mereka menggunakannya pada tahun 1972 untuk mengukur laju cahaya dalam ruang hampa dengan ketidakpastian pecahan 3,5 × 10-9.3,5×10−9.[107][108]
Sejarah[sunting | sunting sumber]
| <1638 | Galileo, lentera tertutup | inkonklusif[catatan 9] |
| <1667 | Accademia del Cimento, lentera tertutup | inkonklusif[catatan 10] |
| 1675 | Rømer dan Huygens, bulan Jupiter | 220.000[85][113] |
| 1729 | James Bradley, aberasi cahaya | 301.000[94] |
| 1849 | Hippolyte Fizeau, roda bergigi | 315.000[94] |
| 1862 | Léon Foucault, cermin berotasi | 298.000±500[94] |
| 1907 | Rosa and Dorsey, konstanta EM | 299.710±30[99][100] |
| 1926 | Albert A. Michelson, cermin berotasi | 299.796±4[114] |
| 1950 | Essen and Gordon-Smith, resonator rongga | 299.792,5±3,0[102] |
| 1958 | K.D. Froome, interferometri radio | 299.792,50±0,10[106] |
| 1972 | Evenson et al., interferometri laser | 299.792,4562±0,0011[108] |
| 1983 | CGPM ke-17, definisi meter | 299.792,458 (eksak)[83] |
Sampai periode modern awal, tidak diketahui apakah cahaya berjalan secara seketika atau pada laju sangat cepat yang terbatas. Penelitian tercatat pertama yang masih ada mengenai hal ini terdapat di Yunani Kuno. Orang-orang Yunani Kuno, cendekiawan Muslim, dan ilmuwan Eropa klasik lama memperdebatkan ini sampai Rømer memberikan perhitungan pertama dari laju cahaya. Teori Relativitas Khusus Einstein menyimpulkan bahwa laju cahaya adalah konstan terlepas dari kerangka acuan pengamatnya. Sejak itu, para ilmuwan telah memberikan pengukuran yang semakin akurat.
Sejarah awal[sunting | sunting sumber]
Empedocles (c. 490-430 SM) adalah orang pertama yang mengusulkan teori cahaya[115] dan mengklaim bahwa cahaya memiliki laju yang terbatas.[116] Ia menyatakan bahwa cahaya adalah sesuatu yang bergerak, dan karena itu memerlukan waktu untuk perjalanan. Aristoteles berpendapat, sebaliknya, bahwa "cahaya adalah karena kehadiran sesuatu, tetapi bukan merupakan gerakan".[117] Euklides dan Ptolemaeus memajukan teori emisi penglihatan Empedocles, di mana cahaya dipancarkan dari mata, sehingga memungkinkan melihat. Berdasarkan teori itu, Heron dari Alexandria berpendapat bahwa laju cahaya harus tak hingga karena objek yang jauh seperti bintang muncul segera setelah membuka mata.
Filsuf awal Islam awalnya setuju dengan pandangan Aristoteles bahwa cahaya tidak memiliki laju perjalanan. Pada tahun 1021, Ibnu Haitsam menerbitkan Kitab Optik, di mana ia menyajikan serangkaian argumen yang menolak teori emisi penglihatan dan mendukung teori intromisi yang sekarang diterima, di mana cahaya bergerak dari objek ke mata.[118] Hal ini menyebabkan Ibnu Haitsam untuk mengusulkan bahwa cahaya harus memiliki laju yang terbatas,[117][119][120] dan bahwa laju cahaya bersifat variabel, menurun dalam benda yang lebih padat.[120][121] Ia berpendapat bahwa cahaya adalah materi substansial, perambatannya membutuhkan waktu, meskipun jika ini tersembunyi dari indra kita.[122] Juga pada abad ke-11, al-Biruni sepakat bahwa cahaya memiliki kecepatan yang terbatas, dan mengamati bahwa laju cahaya jauh lebih cepat dari kelajuan suara.[123]
Pada abad ke-13, Roger Bacon berpendapat bahwa laju cahaya di udara terbatas, menggunakan argumen filosofis yang didukung oleh penulisan Ibnu Haitsam dan Aristoteles.[124][125] Pada tahun 1270-an, Witelo mempertimbangkan kemungkinan cahaya bergerak dengan laju tak hingga dalam ruang hampa, tetapi melambat dalam benda yang lebih padat.[126] Pada abad ke-14, Sayana telah membuat pernyataan tentang laju cahaya dalam komentarnya pada Hindu Regweda.[127]
Pada awal abad ke-17, Johannes Kepler percaya bahwa laju cahaya adalah terbatas, karena ruang kosong tidak memberikan halangan pada cahaya. René Descartes berpendapat bahwa jika laju cahaya terbatas, Matahari, Bumi, dan Bulan akan keluar dari kesejajaran saat gerhana bulan. Karena salah penjajaran tersebut belum diamati, Descartes menyimpulkan laju cahaya adalah terbatas. Descartes berspekulasi bahwa jika laju cahaya terbatas, seluruh sistem filsafatnya mungkin hancur.[117] Dalam penurunan hukum Snellius yang dilakukan Descartes, dia berasumsi bahwa meskipun laju cahaya adalah seketika, semakin padat medium, semakin cepat laju cahaya.[128] Pierre de Fermat menurunkan hukum Snellius menggunakan asumsi yang berlawanan, semakin padat medium semakin lambat cahaya bergerak. Fermat juga mendukung gagasan bahwa cahaya memiliki kecepatan yang terbatas.[129]
Usaha pengukuran pertama[sunting | sunting sumber]
Pada tahun 1629, Isaac Beeckman mengusulkan sebuah percobaan di mana seseorang mengamati kilatan meriam terpantul dari cermin sekitar satu mil (1,6 km) jauhnya. Pada tahun 1638, Galileo Galilei mengusulkan eksperimen, serta mengklaim telah melakukan itu beberapa tahun sebelumnya, untuk mengukur laju cahaya dengan mengamati penundaan antara dibukanya sebuah lentera dan diamatinya pembukaan tersebut di tempat yang agak jauh. Ia tidak dapat membedakan apakah perjalanan cahaya seketika atau tidak, tetapi menyimpulkan bahwa jika tidak, perjalanan tersebut haruslah luar biasa cepat.[109][110] Pada tahun 1667, Accademia del Cimento dari Firenze melaporkan bahwa mereka telah melakukan percobaan Galileo, dengan lentera berjarak sekitar satu mil, tetapi tidak ada penundaan yang diamati. Penundaan yang sebenarnya dalam percobaan ini akan menjadi sekitar 11 mikrodetik.

Perkiraan kuantitatif pertama dari laju cahaya dibuat pada 1676 oleh Rømer (lihat Penentuan laju cahaya oleh Rømer).[84][85] Dari pengamatan bahwa periode bulan terdalam Jupiter Io tampak lebih pendek ketika Bumi mendekati Jupiter daripada ketika menjauhi dari itu, ia menyimpulkan bahwa cahaya berjalan pada laju yang terbatas, dan memperkirakan bahwa cahaya membutuhkan 22 menit untuk menyeberangi diameter orbit bumi. Christiaan Huygens mengkombinasikan perkiraan ini dengan perkiraan diameter orbit bumi untuk mendapatkan perkiraan laju cahaya 220.000 km/s, 26% lebih rendah dari nilai yang sebenarnya.[113]
Pada bukunya tahun 1704 Opticks, Isaac Newton melaporkan perhitungan Rømer untuk laju terbatas cahaya dan memberikan nilai "tujuh atau delapan menit" untuk waktu yang dibutuhkan untuk cahaya untuk perjalanan dari Matahari ke Bumi (nilai modernnya adalah 8 menit 19 detik).[130] Newton bertanya apakah bayangan gerhana Rømer ini berwarna; mendengar bahwa mereka tidak berwarna, ia menyimpulkan warna yang berbeda bergerak pada laju yang sama. Pada 1729, James Bradley menemukan aberasi bintang.[86] Dari efek ini ia menentukan bahwa cahaya harus bergerak 10.210 kali lebih cepat dari Bumi di orbitnya (angka modernnya 10.066 kali lebih cepat) atau, sama, bahwa cahaya akan memerlukan 8 menit 12 detik untuk perjalanan dari Matahari ke Bumi.[86]
Hubungan dengan elektromagnetisme[sunting | sunting sumber]
Pada abad ke-19 Hippolyte Fizeau mengembangkan metode untuk menentukan laju cahaya berdasarkan pengukuran waktu terbang di Bumi dan melaporkan nilai 315.000 km/s. Metodenya diperbaiki oleh Léon Foucault yang memperoleh nilai 298.000 km/s pada tahun 1862.[94] Pada tahun 1856, Wilhelm Eduard Weber dan Rudolf Kohlrausch mengukur rasio unit elektromagnetik dan elektrostatik dari muatan, 1/√ε0μ0, dengan melepaskan muatan dari tabung Leyden, dan menemukan bahwa nilai numeriknya sangat dekat dengan laju cahaya yang diukur langsung oleh Fizeau. Tahun berikutnya Gustav Kirchhoff menghitung bahwa sinyal listrik dalam kawat tanpa hambatan berjalan sepanjang kawat pada kelajuan ini.[131] Pada tahun 1860-an awal, Maxwell menunjukkan bahwa, menurut teori elektromagnetisme yang dia kerjakan, gelombang elektromagnetik merambat di ruang kosong[132][133][134] pada kelajuan yang sama dengan rasio Weber/Kohrausch di atas, dan menarik perhatian terhadap kedekatan numerik dari nilai ini dengan laju cahaya yang diukur oleh Fizeau, ia mengusulkan bahwa cahaya sebenarnya merupakan gelombang elektromagnetik.[135]
Eter sebagai medium cahaya[sunting | sunting sumber]

Pada saat itu diduga bahwa ruang kosong diisi dengan medium latar belakang yang disebut eter (Inggris: luminiferous aether) di mana medan elektromagnetik berada. Beberapa fisikawan berpikir bahwa eter ini bertindak sebagai kerangka terpilih acuan untuk perambatan cahaya dan oleh karena itu seharusnya mungkin untuk mengukur gerakan bumi terhadap medium ini, dengan mengukur isotropi kecepatan cahaya. Dimulai pada tahun 1880-an beberapa percobaan dilakukan untuk mencoba mendeteksi gerakan ini, yang paling terkenal adalah percobaan yang dilakukan oleh Albert A. Michelson dan Edward W. Morley pada tahun 1887.[136] Gerakan yang terdeteksi selalu kurang dari kesalahan pengamatan. Percobaan modern menunjukkan bahwa laju dua arah cahaya adalah isotropik (sama di setiap arah) hingga 6 nanometer per detik.[137] Karena percobaan ini Hendrik Lorentz mengusulkan bahwa gerak aparatus melalui eter dapat menyebabkan aparatus berkontraksi sepanjang panjangnya dalam arah gerakan, dan ia lebih lanjut berasumsi, bahwa variabel waktu untuk sistem bergerak juga harus diubah sesuai ("waktu setempat"), yang menyebabkan perumusan transformasi Lorentz. Berdasarkan teori eter Lorentz ini, Henri Poincaré (1900) menunjukkan bahwa waktu setempat ini (hingga orde pertama dalam v/c) ditunjukkan oleh jam yang bergerak dalam eter, yang disinkronkan dengan asumsi kecepatan cahaya konstan. Pada tahun 1904, ia berspekulasi bahwa laju cahaya bisa menjadi kecepatan pembatas dalam dinamika, asalkan semua asumsi teori Lorentz ini dikonfirmasi. Pada tahun 1905, Poincaré mempersatukan teori eter Lorentz dengan prinsip relativitas.[138][139]
Relativitas khusus[sunting | sunting sumber]
Pada tahun 1905 Einstein mendalilkan dari awal bahwa laju cahaya dalam ruang hampa, diukur oleh pengamat yang tidak dipercepat, tidak bergantung pada gerakan sumber ataupun pengamat. Menggunakan ini dan prinsip relativitas sebagai dasar ia menurunkan teori relativitas khusus, di mana laju cahaya dalam ruang hampa c menjadi sebuah konstanta dasar, juga muncul dalam konteks yang tidak terkait dengan cahaya. Hal ini membuat konsep eter stasioner (yang masih dianut Lorentz dan Poincare) tidak berguna dan merevolusi konsep ruang dan waktu.[140][141]
Peningkatan akurasi c dan redefinisi meter dan detik[sunting | sunting sumber]
Pada paruh kedua abad ke-20 banyak kemajuan dibuat dalam meningkatkan akurasi pengukuran laju cahaya, pertama dengan teknik resonansi rongga dan kemudian dengan teknik interferometer laser. Ini dibantu oleh definisi meter dan detik yang baru dan lebih tepat. Pada tahun 1950, Louis Essen menentukan laju cahaya sebagai 299.792,5±1 km/s, menggunakan resonansi rongga. Nilai ini diadopsi oleh Majelis Umum ke-12 dari Radio-Scientific Union pada tahun 1957. Pada tahun 1960, meter didefinisikan kembali berdasarkan panjang gelombang garis spektrum tertentu kripton-86, dan, pada tahun 1967, detik didefinisikan kembali berdasarkan frekuensi transisi hiperhalus dari keadaan dasar sesium-133.
Pada tahun 1972, menggunakan metode laser interferometer dan definisi baru, sebuah kelompok di NBS di Boulder, Colorado menentukan laju cahaya dalam ruang hampa menjadi c = 299.792.456,2±1,1 m/s. Ini adalah 100 kali lebih pasti dari nilai yang diterima sebelumnya. Ketidakpastian yang tersisa terutama terkait dengan definisi meter.[catatan 11][108] Karena percobaan serupa menemukan hasil yang sebanding untuk c, Konferensi Umum mengenai Berat dan Ukuran (Prancis: Conférence générale des poids et mesures, CGPM) ke-15 pada tahun 1975 merekomendasikan menggunakan nilai 299.792.458 m/s untuk laju cahaya.[144]
Mendefinisikan laju cahaya sebagai konstanta eksplisit[sunting | sunting sumber]
Pada tahun 1983 CGPM ke-17 menemukan bahwa panjang gelombang dari pengukuran frekuensi dan nilai yang diberikan untuk laju cahaya lebih dapat direproduksi dari standar sebelumnya. Mereka mempertahankan definisi detik tahun 1967, sehingga frekuensi hiperhalus sesium sekarang akan menentukan baik detik dan meter. Untuk melakukan hal ini, mereka mendefinisikan ulang meter sebagai: "Meter adalah panjang jarak yang ditempuh oleh cahaya dalam ruang hampa selama selang waktu dari 1/299.792.458 detik."[83] Sebagai hasil dari definisi ini, nilai laju cahaya dalam ruang hampa adalah secara eksak 299.792.458 m/s[145][146] dan telah menjadi konstanta yang didefinisikan dalam sistem satuan SI.[11] Peningkatan teknik eksperimental yang sebelum 1983 akan mengukur laju cahaya, tidak lagi memengaruhi nilai yang diketahui dari laju cahaya dalam satuan SI, melainkan memungkinkan realisasi yang lebih tepat dari meter dengan secara lebih akurat mengukur panjang gelombang Kripton-86 dan sumber cahaya lainnya.[147][148]
Pada tahun 2011, CGPM menyatakan niatnya untuk mendefinisikan ketujuh satuan pokok SI menggunakan apa yang disebut "formulasi konstanta eksplisit", di mana setiap "satuan didefinisikan secara tidak langsung dengan menentukan secara eksplisit nilai yang pasti untuk sebuah konstanta dasar yang diakui", seperti yang dilakukan untuk laju cahaya. CGPM mengusulkan kata-kata dari definisi meter yang baru, tetapi setara: "Meter, simbol m, adalah satuan panjang; besarnya diatur dengan menetapkan nilai numerik dari laju cahaya dalam ruang hampa untuk menjadi sama dengan secara eksak 299.792.458 bila dinyatakan dalam satuan SI m s−1."[149] Ini adalah salah satu perubahan yang dimasukkan dalam redefinisi satuan pokok SI 2019 yang juga disebut SI Baru.[150]
Lihat pula[sunting | sunting sumber]
Catatan[sunting | sunting sumber]
- ^ Nilai eksak:
(299.792.458 × 60 × 60 × 24 / 149.597.870.700) SA/hari - ^ Nilai eksak: (999.992.651π / 10.246.429.500) pc/tahun
- ^ Laju cahaya dalam satuan imperial dan satuan Amerika Serikat berdasarkan inci yang secara eksak 2,54 cm dan secara eksak 186.282 mil, 698 yard, 2 kaki, dan 5 21127 inci per detik.[12]
- ^ Namun, frekuensi dari cahaya dapat bergantung pada gerakan sumber relatif dengan pengamat, dikarenakan efek Doppler.
- ^ Meskipun objek bergerak terukur lebih pendek di sepanjang garis gerak relatif, mereka juga tampak berotasi. Efek ini, disebut rotasi Terrell, dikarenakan waktu yang berbeda-beda yang diperlukan cahaya dari bagian-bagian yang berbeda dari objek untuk mencapai pengamat.[21][22]
- ^ Efek Scharnhorst membolehkan sinyal untuk berjalan sedikit lebih cepat dari c, tetapi kondisi khusus di mana efek ini dapat terjadi mencegah seseorang menggunakan efek ini untuk melanggar kausalitas.[36]
- ^ Satuan astronomi sebelumnya didefinisikan sebagai jari-jari orbit Newton sirkuler tidak terganggu mengelilingi Matahari dari partikel dengan massa infinitesimal, bergerak dengan frekuensi sudut 0.01720209895 radian (sekitar ⅟365,256898 dari revolusi) per hari.[90]
- ^ Walaupun begitu, pada tingkat ketelitian ini, efek dari relativitas umum harus dipertimbangkan ketika menafsirkan panjang. Meter dianggap sebagai satuan panjang wajar, sedangkan SA biasanya digunakan sebagai satuan panjang yang diamati dalam kerangka acuan yang diberikan. Nilai-nilai yang dikutip di sini mengikuti konvensi terakhir, dan kompatibel dengan TDB.[92]
- ^ Galilei (1954),[109] Boyer (1941),[110] Foschi & Leone (2009, p.1252).[111] Menurut Galileo, lentera yang digunakannya adalah "pada jarak pendek, kurang dari satu mil." Dengan asumsi jarak tidak terlalu lebih pendek dari satu mil, dan bahwa "sekitar 1/30 detik adalah selang waktu minimum yang dapat dibedakan oleh mata telanjang", Boyer mencatat bahwa percobaan Galileo bisa dikatakan telah menetapkan batas bawah sekitar 60 mil per detik untuk kecepatan cahaya.
- ^ Magalotti (1667, pp.265–6),[112] Foschi & Leone (2009, p.1253).[111]
- ^ Antara tahun 1960 dan 1983 meter didefinisikan sebagai: "Meter adalah panjang yang sama dengan 1.650.763,73 panjang gelombang dalam vakum dari radiasi yang sesuai dengan transisi antara tingkatan 2p10 dan 5d5 dari atom kripton 86."[142] Ditemukan pada tahun 1970-an bahwa garis spektral ini tidak simetris, yang memberikan batasan pada presisi dengan itu definisi dapat direalisasikan dalam percobaan interferometri.[143]
Referensi[sunting | sunting sumber]
- ^ Penrose, R (2004). The Road to Reality: A Complete Guide to the Laws of the Universe. Vintage Books. hlm. 410–1. ISBN 9780679776314.
... the most accurate standard for the metre is conveniently defined so that there are exactly 299,792,458 of them to the distance travelled by light in a standard second, giving a value for the metre that very accurately matches the now inadequately precise standard metre rule in Paris.
- ^ Uzan, J-P; Leclercq, B (2008). The Natural Laws of the Universe: Understanding Fundamental Constants. Springer. hlm. 43–4. ISBN 0387734546.
- ^ "How is the speed of light measured?".
- ^ a b Stachel, JJ (2002). Einstein from "B" to "Z" – Volume 9 of Einstein studies. Springer. hlm. 226. ISBN 0-8176-4143-2.
- ^ a b Biro Internasional untuk Ukuran dan Timbangan (2006), Sistem Satuan Internasional [Le Système international d'unités; The International System of Units] (PDF) (dalam bahasa Prancis and Inggris) (edisi ke-8), hlm. 112, ISBN 92-822-2213-6, diarsipkan dari versi asli (PDF) tanggal 2017-08-14
- ^ Gibbs, P (2004) [1997]. "Why is c the symbol for the speed of light?". Usenet Physics FAQ. University of California, Riverside. Diarsipkan dari versi asli tanggal 2009-11-17. Diakses tanggal 2009-11-16. "The origins of the letter c being used for the speed of light can be traced back to a paper of 1856 by Weber and Kohlrausch [...] Weber apparently meant c to stand for 'constant' in his force law, but there is evidence that physicists such as Lorentz and Einstein were accustomed to a common convention that c could be used as a variable for velocity. This usage can be traced back to the classic Latin texts in which c stood for 'celeritas' meaning 'speed'."
- ^ Mendelson, KS (2006). "The story of c". American Journal of Physics. 74 (11): 995–997. Bibcode:2006AmJPh..74..995M. doi:10.1119/1.2238887.
- ^ Lihat sebagai contoh:
- Lide, DR (2004). CRC Handbook of Chemistry and Physics. CRC Press. hlm. 2–9. ISBN 0-8493-0485-7.
- Harris, JW; et al. (2002). Handbook of Physics. Springer. hlm. 499. ISBN 0-387-95269-1.
- Whitaker, JC (2005). The Electronics Handbook. CRC Press. hlm. 235. ISBN 0-8493-1889-0.
- Cohen, ER; et al. (2007). Quantities, Units and Symbols in Physical Chemistry (edisi ke-3rd). Royal Society of Chemistry. hlm. 184. ISBN 0-85404-433-7.
- ^
Sydenham, PH (2003). "Measurement of length". Dalam Boyes, W. Instrumentation Reference Book (edisi ke-3rd). Butterworth–Heinemann. hlm. 56. ISBN 0-7506-7123-8.
... if the speed of light is defined as a fixed number then, in principle, the time standard will serve as the length standard ...
- ^ "CODATA value: Speed of Light in Vacuum". The NIST reference on Constants, Units, and Uncertainty. NIST. Diakses tanggal 2009-08-21.
- ^ a b Jespersen, J; Fitz-Randolph, J; Robb, J (1999). From Sundials to Atomic Clocks: Understanding Time and Frequency (edisi ke-Reprint of National Bureau of Standards 1977, 2nd). Courier Dover. hlm. 280. ISBN 0-486-40913-9.
- ^ Savard, J. "From Gold Coins to Cadmium Light". John Savard. Diarsipkan dari versi asli tanggal 2009-11-14. Diakses tanggal 2009-11-14.
- ^ Lawrie, ID (2002). "Appendix C: Natural units". A Unified Grand Tour of Theoretical Physics (edisi ke-2nd). CRC Press. hlm. 540. ISBN 0-7503-0604-1.
- ^ Hsu, L (2006). "Appendix A: Systems of units and the development of relativity theories". A Broader View of Relativity: General Implications of Lorentz and Poincaré Invariance (edisi ke-2nd). World Scientific. hlm. 427–8. ISBN 981-256-651-1.
- ^ Einstein, A (1905). "Zur Elektrodynamik bewegter Körper". Annalen der Physik (dalam bahasa German). 17: 890–921. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004. terjemahan bahasa Inggris: Perrett, W; Jeffery, GB (tr.); Walker, J (ed.). "On the Electrodynamics of Moving Bodies". Fourmilab. Diakses tanggal 2009-11-27.
- ^ Hsu, J-P; Zhang, YZ (2001). Lorentz and Poincaré Invariance. Advanced Series on Theoretical Physical Science. 8. World Scientific. hlm. 543ff. ISBN 981-02-4721-4.
- ^ a b Zhang, YZ (1997). Special Relativity and Its Experimental Foundations. Advanced Series on Theoretical Physical Science. 4. World Scientific. hlm. 172–3. ISBN 981-02-2749-3. Diarsipkan dari versi asli tanggal 2012-05-19. Diakses tanggal 2016-01-09.
- ^ d'Inverno, R (1992). Introducing Einstein's Relativity. Oxford University Press. hlm. 19–20. ISBN 0-19-859686-3.
- ^ Sriranjan, B (2004). "Postulates of the special theory of relativity and their consequences". The Special Theory to Relativity. PHI Learning Pvt. Ltd. hlm. 20 ff. ISBN 81-203-1963-X.
- ^ Roberts, T; Schleif, S; Dlugosz, JM (ed.) (2007). "What is the experimental basis of Special Relativity?". Usenet Physics FAQ. University of California, Riverside. Diakses tanggal 2009-11-27.
- ^ Terrell, J (1959). "Invisibility of the Lorentz Contraction". Physical Review. 116 (4): 1041–5. Bibcode:1959PhRv..116.1041T. doi:10.1103/PhysRev.116.1041.
- ^ Penrose, R (1959). "The Apparent Shape of a Relativistically Moving Sphere". Proceedings of the Cambridge Philosophical Society. 55 (01): 137–9. Bibcode:1959PCPS...55..137P. doi:10.1017/S0305004100033776.
- ^ Hartle, JB (2003). Gravity: An Introduction to Einstein's General Relativity. Addison-Wesley. hlm. 52–9. ISBN 981-02-2749-3.
- ^ Hartle, JB (2003). Gravity: An Introduction to Einstein's General Relativity. Addison-Wesley. hlm. 332. ISBN 981-02-2749-3.
- ^ The interpretation of observations on binary systems used to determine the speed of gravity is considered doubtful by some authors, leaving the experimental situation uncertain; seeSchäfer, G; Brügmann, MH (2008). "Propagation of light in the gravitational filed of binary systems to quadratic order in Newton's gravitational constant: Part 3: 'On the speed-of-gravity controversy'". Dalam Dittus, H; Lämmerzahl, C; Turyshev, SG. Lasers, clocks and drag-free control: Exploration of relativistic gravity in space. Springer. ISBN 3-540-34376-8.
- ^ a b Gibbs, P (1997) [1996]. Carlip, S, ed. "Is The Speed of Light Constant?". Usenet Physics FAQ. University of California, Riverside. Diarsipkan dari versi asli tanggal 2009-11-17. Diakses tanggal 2009-11-26.
- ^
Ellis, GFR; Uzan, J-P (2005). "'c' is the speed of light, isn't it?". American Journal of Physics. 73 (3): 240–7. arXiv:gr-qc/0305099
 . Bibcode:2005AmJPh..73..240E. doi:10.1119/1.1819929.
. Bibcode:2005AmJPh..73..240E. doi:10.1119/1.1819929. The possibility that the fundamental constants may vary during the evolution of the universe offers an exceptional window onto higher dimensional theories and is probably linked with the nature of the dark energy that makes the universe accelerate today.
- ^ An overview can be found in the dissertation of Mota, DF (2006). "Variations of the fine structure constant in space and time". arΧiv:astro-ph/0401631 [astro-ph].
- ^
Uzan, J-P (2003). "The fundamental constants and their variation: observational status and theoretical motivations". Reviews of Modern Physics. 75 (2): 403. arXiv:hep-ph/0205340
 . Bibcode:2003RvMP...75..403U. doi:10.1103/RevModPhys.75.403.
. Bibcode:2003RvMP...75..403U. doi:10.1103/RevModPhys.75.403.
- ^ Amelino-Camelia, G (2008). "Quantum Gravity Phenomenology". arΧiv:0806.0339 [gr-qc].
- ^ Herrmann, S; et al. (2009). "Rotating optical cavity experiment testing Lorentz invariance at the 10−17 level". Physical Review D. 80 (100): 105011. arXiv:1002.1284
 . Bibcode:2009PhRvD..80j5011H. doi:10.1103/PhysRevD.80.105011.
. Bibcode:2009PhRvD..80j5011H. doi:10.1103/PhysRevD.80.105011.
- ^ Lang, KR (1999). Astrophysical formulae (edisi ke-3rd). Birkhäuser. hlm. 152. ISBN 3-540-29692-1.
- ^ It's official: Time machines won't work, Los Angeles Times July 25 2011
- ^ HKUST Professors Prove Single Photons Do Not Exceed the Speed of Light
- ^ Fowler, M (March 2008). "Notes on Special Relativity" (PDF). Universitas Virginia. hlm. 56. Diakses tanggal 2010-05-07.
- ^
Liberati, S; Sonego, S; Visser, M (2002). "Faster-than-c signals, special relativity, and causality". Annals of Physics. 298 (1): 167–85. arXiv:gr-qc/0107091
 . Bibcode:2002AnPhy.298..167L. doi:10.1006/aphy.2002.6233.
. Bibcode:2002AnPhy.298..167L. doi:10.1006/aphy.2002.6233.
- ^ Taylor, EF; Wheeler, JA (1992). Spacetime Physics. W. H. Freeman. hlm. 74–5. ISBN 0-7167-2327-1.
- ^ Tolman, RC (2009) [1917]. "Velocities greater than that of light". The Theory of the Relativity of Motion (edisi ke-Reprint). BiblioLife. hlm. 54. ISBN 978-1-103-17233-7.
- ^ Hecht, E (1987). Optics (edisi ke-2nd). Addison-Wesley. hlm. 62. ISBN 0-201-11609-X.
- ^ Quimby, RS (2006). Photonics and lasers: an introduction. John Wiley and Sons. hlm. 9. ISBN 978-0-471-71974-8.
- ^ Wertheim, M (2007-06-20). "The Shadow Goes". The New York Times. Diakses tanggal 2009-08-21.
- ^ a b c d Gibbs, P (1997). "Is Faster-Than-Light Travel or Communication Possible?". Usenet Physics FAQ. University of California, Riverside. Diarsipkan dari versi asli tanggal 2009-11-17. Diakses tanggal 2008-08-20.
- ^ Sakurai, JJ (1994). T, S, ed. Modern Quantum Mechanics (edisi ke-Revised). Addison-Wesley. hlm. 231–232. ISBN 0-201-53929-2.
- ^ Muga, JG; Mayato, RS; Egusquiza, IL, eds (2007). Time in Quantum Mechanics. Springer. hlm. 48. ISBN 3-540-73472-4.
- ^ Hernández-Figueroa, HE; Zamboni-Rached, M; Recami, E (2007). Localized Waves. Wiley Interscience. hlm. 26. ISBN 0-470-10885-1.
- ^ Wynne, K (2002). "Causality and the nature of information" (PDF). Optics Communications. 209 (1–3): 84–100. Bibcode:2002OptCo.209...85W. doi:10.1016/S0030-4018(02)01638-3.[pranala nonaktif permanen] archive
- ^ Rees, M (1966). "The Appearance of Relativistically Expanding Radio Sources". Nature. 211 (5048): 468. Bibcode:1966Natur.211..468R. doi:10.1038/211468a0.
- ^ Chase, IP. "Apparent Superluminal Velocity of Galaxies". Usenet Physics FAQ. University of California, Riverside. Diakses tanggal 2009-11-26.
- ^ Harrison, ER (2003). Masks of the Universe. Cambridge University Press. hlm. 206. ISBN 0-521-77351-2.
- ^ Panofsky, WKH; Phillips, M (1962). Classical Electricity and Magnetism. Addison-Wesley. hlm. 182. ISBN 978-0-201-05702-7.
- ^
Schaefer, BE (1999). "Severe limits on variations of the speed of light with frequency". Physical Review Letters. 82 (25): 4964–6. arXiv:astro-ph/9810479
 . Bibcode:1999PhRvL..82.4964S. doi:10.1103/PhysRevLett.82.4964.
. Bibcode:1999PhRvL..82.4964S. doi:10.1103/PhysRevLett.82.4964.
- ^
Ellis, J; Mavromatos, NE; Nanopoulos, DV; Sakharov, AS (2003). "Quantum-Gravity Analysis of Gamma-Ray Bursts using Wavelets". Astronomy & Astrophysics. 402 (2): 409–24. arXiv:astro-ph/0210124
 . Bibcode:2003A&A...402..409E. doi:10.1051/0004-6361:20030263.
. Bibcode:2003A&A...402..409E. doi:10.1051/0004-6361:20030263.
- ^ Füllekrug, M (2004). "Probing the Speed of Light with Radio Waves at Extremely Low Frequencies". Physical Review Letters. 93 (4): 043901. Bibcode:2004PhRvL..93d3901F. doi:10.1103/PhysRevLett.93.043901.
- ^ a b Adelberger, E; Dvali, G; Gruzinov, A (2007). "Photon Mass Bound Destroyed by Vortices". Physical Review Letters. 98 (1): 010402. arXiv:hep-ph/0306245
 . Bibcode:2007PhRvL..98a0402A. doi:10.1103/PhysRevLett.98.010402. PMID 17358459.
. Bibcode:2007PhRvL..98a0402A. doi:10.1103/PhysRevLett.98.010402. PMID 17358459.
- ^ Sidharth, BG (2008). The Thermodynamic Universe. World Scientific. hlm. 134. ISBN 981-281-234-2.
- ^ Amelino-Camelia, G (2009). "Astrophysics: Burst of support for relativity". Nature. 462 (7271): 291–292. Bibcode:2009Natur.462..291A. doi:10.1038/462291a. PMID 19924200. Ringkasan – Nature (19 November 2009).
- ^ de Podesta, M (2002). Understanding the Properties of Matter. CRC Press. hlm. 131. ISBN 0-415-25788-3.
- ^ "Refractive index of Water, H20 [Liquids]". refractiveindex.info. Mikhail Polyanskiy. Diakses tanggal 2010-03-14.
- ^ "Refractive index of Fused Silica [Glasses]". refractiveindex.info. Mikhail Polyanskiy. Diakses tanggal 2010-03-14.
- ^ "Refractive index of C [Crystals etc.]". refractiveindex.info. Mikhail Polyanskiy. Diakses tanggal 2010-03-14.
- ^ Harvard News Office (2001-01-24). "Harvard Gazette: Researchers now able to stop, restart light". News.harvard.edu. Diakses tanggal 2011-11-08.
- ^ Milonni, PW (2004). Fast light, slow light and left-handed light. CRC Press. hlm. 25. ISBN 0-7503-0926-1.
- ^ Toll, JS (1956). "Causality and the Dispersion Relation: Logical Foundations". Physical Review. 104 (6): 1760–1770. Bibcode:1956PhRv..104.1760T. doi:10.1103/PhysRev.104.1760.
- ^ Hau, LV; Harris, SE; Dutton, Z; Behroozi, CH (1999). "Light speed reduction to 17 metres per second in an ultracold atomic gas" (PDF). Nature. 397 (6720): 594–598. Bibcode:1999Natur.397..594V. doi:10.1038/17561.
- ^ Liu, C; Dutton, Z; Behroozi, CH; Hau, LV (2001). "Observation of coherent optical information storage in an atomic medium using halted light pulses" (PDF). Nature. 409 (6819): 490–493. Bibcode:2001Natur.409..490L. doi:10.1038/35054017. PMID 11206540.
- ^
Bajcsy, M; Zibrov, AS; Lukin, MD (2003). "Stationary pulses of light in an atomic medium". Nature. 426 (6967): 638–41. arXiv:quant-ph/0311092
 . Bibcode:2003Natur.426..638B. doi:10.1038/nature02176. PMID 14668857.
. Bibcode:2003Natur.426..638B. doi:10.1038/nature02176. PMID 14668857.
- ^ Dumé, B (2003). "Switching light on and off". Physics World. Institute of Physics. Diarsipkan dari versi asli tanggal 2008-12-05. Diakses tanggal 2008-12-08.
- ^ Whitehouse, D (19 July 2000). "Beam Smashes Light Barrier". BBC News. Diakses tanggal 2008-12-08.
- ^ a b Milonni, PW (2004). "2". Fast light, slow light and left-handed light. CRC Press. ISBN 0-7503-0926-1.
- ^ Cherenkov, Pavel A. (1934). "Видимое свечение чистых жидкостей под действием γ-радиации". Doklady Akademii Nauk SSSR. 2: 451. Reprinted in Usp. Fiz. Nauk 93 (1967) 385, and in "Pavel Alekseyevich Čerenkov: Chelovek i Otkrytie" A. N. Gorbunov, E. P. Čerenkova (eds.), Moscow, Nauka (1999) pp. 149–153.
- ^ Parhami, B (1999). Introduction to parallel processing: algorithms and architectures. Plenum Press. hlm. 5. ISBN 978-0-306-45970-2. dan Imbs, D; Raynal, Michel (2009). Malyshkin, V, ed. Software Transactional Memories: An Approach for Multicore Programming. 10th International Conference, PaCT 2009, Novosibirsk, Russia, August 31 – September 4, 2009. Springer. hlm. 26. ISBN 978-3-642-03274-5.
- ^ Nilai indeks dari serat optik biasanya di antara 1,518 dan 1,538: Midwinter, JE (1991). Optical Fibers for Transmission (edisi ke-2nd). Krieger Publishing Company. ISBN 0-89464-595-1.
- ^ "Theoretical vs real-world speed limit of Ping". Royal Pingdom. Pingdom. June 2007. Diarsipkan dari versi asli tanggal 2010-09-02. Diakses tanggal 2010-05-05.
- ^ "Day 4: Lunar Orbits 7, 8 and 9". The Apollo 8 Flight Journal. NASA. Diarsipkan dari versi asli tanggal 2011-01-04. Diakses tanggal 2010-12-16.
- ^ a b "Hubble Reaches the "Undiscovered Country" of Primeval Galaxies" (Siaran pers). Space Telescope Science Institute. 5 January 2010.
- ^ "The Hubble Ultra Deep Field Lithograph" (PDF). NASA. Diakses tanggal 2010-02-04.
- ^ "The IAU and astronomical units". International Astronomical Union. Diakses tanggal 2010-10-11.
- ^ Further discussion can be found at "StarChild Question of the Month for March 2000". StarChild. NASA. 2000. Diakses tanggal 2009-08-22.
- ^ Dickey, JO; et al. (July 1994). "Lunar Laser Ranging: A Continuing Legacy of the Apollo Program". Science. 265 (5171): 482–490. Bibcode:1994Sci...265..482D. doi:10.1126/science.265.5171.482. PMID 17781305.
- ^ Standish, EM (February 1982). "The JPL planetary ephemerides". Celestial Mechanics. 26 (2): 181–186. Bibcode:1982CeMec..26..181S. doi:10.1007/BF01230883.
- ^ Berner, JB; Bryant, SH; Kinman, PW (November 2007). "Range Measurement as Practiced in the Deep Space Network". Proceedings of the IEEE. 95 (11): 2202–2214. doi:10.1109/JPROC.2007.905128.
- ^ "Time is money when it comes to microwaves". Financial Times. 10 May 2013. Diakses tanggal 25 April 2014.
- ^ a b c "Resolution 1 of the 17th CGPM". BIPM. 1983. Diakses tanggal 2009-08-23.
- ^ a b Cohen, IB (1940). "Roemer and the first determination of the velocity of light (1676)". Isis. 31 (2): 327–79. doi:10.1086/347594.
- ^ a b c
"Touchant le mouvement de la lumiere trouvé par M. Rŏmer de l'Académie Royale des Sciences" (PDF). Journal des sçavans (dalam bahasa French): 233–36. 1676.
Diterjemahkan dalam "On the Motion of Light by M. Romer". Philosophical Transactions of the Royal Society. 12 (136): 893–95. 1677. doi:10.1098/rstl.1677.0024. (Sebagaimana dihasilkan ulang di Hutton, C; Shaw, G; Pearson, R eds. (1809). "On the Motion of Light by M. Romer". The Philosophical Transactions of the Royal Society of London, from Their Commencement in 1665, in the Year 1800: Abridged. 2. London: C. & R. Baldwin. hlm. 397–98.)
Laporan yang diterbitkan dalam Journal des sçavans didasarkan pada laporan yang dibacakan oleh Rømer kepada Akademi Sains Prancis pada November 1676 (Cohen, 1940, p. 346). - ^ a b c d Bradley, J (1729). "Account of a new discoved Motion of the Fix'd Stars". Philosophical Transactions. 35: 637–660.
- ^ Duffett-Smith, P (1988). Practical Astronomy with your Calculator. Cambridge University Press. hlm. 62. ISBN 0-521-35699-7. Extract of page 62
- ^ a b "Resolution B2 on the re-definition of the astronomical unit of length" (PDF). International Astronomical Union. 2012.
- ^ "The International System of Units, Supplement 2014: Updates to the 8th edition (2006) of the SI Brochure" (PDF). International Bureau of Weights and Measures. 2014: 14.
- ^ Biro Internasional untuk Ukuran dan Timbangan (2006), Sistem Satuan Internasional [Le Système international d'unités; The International System of Units] (PDF) (dalam bahasa Prancis and Inggris) (edisi ke-8), hlm. 126, ISBN 92-822-2213-6, diarsipkan dari versi asli (PDF) tanggal 2017-08-14
- ^ Pitjeva, EV; Standish, EM (2009). "Proposals for the masses of the three largest asteroids, the Moon–Earth mass ratio and the Astronomical Unit". Celestial Mechanics and Dynamical Astronomy. 103 (4): 365–372. Bibcode:2009CeMDA.103..365P. doi:10.1007/s10569-009-9203-8.
- ^ a b IAU Working Group on Numerical Standards for Fundamental Astronomy. "IAU WG on NSFA Current Best Estimates". US Naval Observatory. Diarsipkan dari versi asli tanggal 2009-12-08. Diakses tanggal 2009-09-25.
- ^ "NPL's Beginner's Guide to Length". UK National Physical Laboratory. Diarsipkan dari versi asli tanggal 2010-08-31. Diakses tanggal 2009-10-28.
- ^ a b c d e Gibbs, P (1997). "How is the speed of light measured?". Usenet Physics FAQ. University of California, Riverside. Diakses tanggal 2010-01-13.
- ^ Fowler, M. "The Speed of Light". Universitas Virginia. Diakses tanggal 2010-04-21.
- ^ Cooke, J; Martin, M; McCartney, H; Wilf, B (1968). "Direct determination of the speed of light as a general physics laboratory experiment". American Journal of Physics. 36 (9): 847. Bibcode:1968AmJPh..36..847C. doi:10.1119/1.1975166.
- ^
Aoki, K; Mitsui, T (2008). "A small tabletop experiment for a direct measurement of the speed of light". American Journal of Physics. 76 (9): 812–815. arXiv:0705.3996
 . Bibcode:2008AmJPh..76..812A. doi:10.1119/1.2919743.
. Bibcode:2008AmJPh..76..812A. doi:10.1119/1.2919743.
- ^ James, MB; Ormond, RB; Stasch, AJ (1999). "Speed of light measurement for the myriad". American Journal of Physics. 67 (8): 681–714. Bibcode:1999AmJPh..67..681J. doi:10.1119/1.19352.
- ^ a b c d e Essen, L; Gordon-Smith, AC (1948). "The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator". Proceedings of the Royal Society of London A. 194 (1038): 348–361. Bibcode:1948RSPSA.194..348E. doi:10.1098/rspa.1948.0085. JSTOR 98293.
- ^ a b Rosa, EB; Dorsey, NE (1907). "The Ratio of the Electromagnetic and Electrostatic Units". Bulletin of the Bureau of Standards. 3 (6): 433. Bibcode:1906PhRvI..22..367R. doi:10.1103/PhysRevSeriesI.22.367.
- ^ Essen, L (1947). "Velocity of Electromagnetic Waves". Nature. 159 (4044): 611–612. Bibcode:1947Natur.159..611E. doi:10.1038/159611a0.
- ^ a b Essen, L (1950). "The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator". Proceedings of the Royal Society of London A. 204 (1077): 260–277. Bibcode:1950RSPSA.204..260E. doi:10.1098/rspa.1950.0172. JSTOR 98433.
- ^ Stauffer, RH (April 1997). "Finding the Speed of Light with Marshmallows". The Physics Teacher. American Association of Physics Teachers. 35 (4): 231. Bibcode:1997PhTea..35..231S. doi:10.1119/1.2344657. Diakses tanggal 2010-02-15.
- ^ "BBC Look East at the speed of light". BBC Norfolk website. BBC. Diakses tanggal 2010-02-15.
- ^ Diskusi rinci mengenai interferometer dan penggunaannya untuk menentukan laju cahaya bisa ditemukan di Vaughan, JM (1989). The Fabry-Perot interferometer. CRC Press. hlm. 47, pp. 384–391. ISBN 0-85274-138-3.
- ^ a b Froome, KD (1958). "A New Determination of the Free-Space Velocity of Electromagnetic Waves". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. The Royal Society. 247 (1248): 109–122. Bibcode:1958RSPSA.247..109F. doi:10.1098/rspa.1958.0172. JSTOR 100591.
- ^ a b Sullivan, DB (2001). "Speed of Light from Direct Frequency and Wavelength Measurements". Dalam Lide, DR. A Century of Excellence in Measurements, Standards, and Technology (PDF). CRC Press. hlm. 191–193. ISBN 0-8493-1247-7. Diarsipkan dari versi asli (PDF) tanggal 2009-08-13. Diakses tanggal 2016-04-25.
- ^ a b c Evenson, KM; et al. (1972). "Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser". Physical Review Letters. 29 (19): 1346–49. Bibcode:1972PhRvL..29.1346E. doi:10.1103/PhysRevLett.29.1346.
- ^ a b Galilei, G (1954) [1638]. Dialogues Concerning Two New Sciences. Crew, H; de Salvio A (trans.). Dover Publications. hlm. 43. ISBN 0-486-60099-8.
- ^ a b Boyer, CB (1941). "Early Estimates of the Velocity of Light". Isis. 33 (1): 24. doi:10.1086/358523.
- ^ a b Foschi, Renato; Leone, Matteo (2009), "Galileo, measurement of the velocity of light, and the reaction times" (PDF), Perception, 38: 1251–9, doi:10.1068/p6263, diakses tanggal 2015-09-25[pranala nonaktif permanen]
- ^ Magalotti, Lorenzo (2001) [1667], Saggi di Naturali Esperienze fatte nell' Accademia del Cimento (edisi ke-digital, online), Florence: Istituto e Museo di Storia delle Scienze, diakses tanggal 2015-09-25
- ^ a b Huygens, C (1690). Traitée de la Lumière (dalam bahasa French). Pierre van der Aa. hlm. 8–9.
- ^ Michelson, A. A. (1927). "Measurement of the Velocity of Light Between Mount Wilson and Mount San Antonio". The Astrophysical Journal. 65: 1. Bibcode:1927ApJ....65....1M. doi:10.1086/143021.
- ^ Weiner, John; Nunes, Frederico (2013). Light-Matter Interaction: Physics and Engineering at the Nanoscale (edisi ke-illustrated). OUP Oxford. hlm. 1. ISBN 978-0-19-856766-0. Extract of page 1
- ^ Sarton, G (1993). Ancient science through the golden age of Greece. Courier Dover. hlm. 248. ISBN 0-486-27495-0.
- ^ a b c MacKay, RH; Oldford, RW (2000). "Scientific Method, Statistical Method and the Speed of Light". Statistical Science. 15 (3): 254–78. doi:10.1214/ss/1009212817. (tekan "Historical background" di daftar isi)
- ^ Gross, CG (1999). "The Fire That Comes from the Eye". Neuroscientist. 5: 58–49. doi:10.1177/107385849900500108.
- ^ Hamarneh, S (1972). "Review: Hakim Mohammed Said, Ibn al-Haitham". Isis. 63 (1): 119. doi:10.1086/350861.
- ^ a b Lester, PM (2005). Visual Communication: Images With Messages. Thomson Wadsworth. hlm. 10–11. ISBN 0-534-63720-5.
- ^ O'Connor, JJ; Robertson, EF. "Abu Ali al-Hasan ibn al-Haytham". Arsip MacTutor History of Mathematics. Universitas St Andrews. Diakses tanggal 2010-01-12.
- ^ Lauginie, P (2005). "Measuring: Why? How? What?" (PDF). Proceedings of the 8th International History, Philosophy, Sociology & Science Teaching Conference. Diarsipkan dari versi asli (PDF) tanggal 2007-01-18. Diakses tanggal 2008-07-18.
- ^ O'Connor, JJ; Robertson, EF. "Abu han Muhammad ibn Ahmad al-Biruni". Arsip MacTutor History of Mathematics. Universitas St Andrews. Diakses tanggal 2010-01-12.
- ^ Lindberg, DC (1996). Roger Bacon and the origins of Perspectiva in the Middle Ages: a critical edition and English translation of Bacon's Perspectiva, with introduction and notes. Oxford University Press. hlm. 143. ISBN 0-19-823992-0.
- ^ Lindberg, DC (1974). "Late Thirteenth-Century Synthesis in Optics". Dalam Edward Grant. A source book in medieval science. Harvard University Press. hlm. 396. ISBN 978-0-674-82360-0.
- ^ Marshall, P (1981). "Nicole Oresme on the Nature, Reflection, and Speed of Light". Isis. 72 (3): 357–74 [367–74]. doi:10.1086/352787.
- ^ "Salinan arsip" (PDF). Diarsipkan dari versi asli (PDF) tanggal 2016-06-02. Diakses tanggal 2016-04-27.
- ^ Florian Cajori, A History of Physics in its Elementary Branches: Including the Evolution of Physical Laboratories (1922)
- ^ Carl Benjamin Boyer, The Rainbow: From Myth to Mathematics (1959)
- ^ Newton, I (1704). "Prop. XI". Optiks. Teks Prop. XI serupa baik di edisi pertama (1704) maupun kedua (1719).
- ^ Kirchhoff, G (1857). "Über die Bewegung der Elektricität". Ann. Phys. 178: 529–544. doi:10.1002/andp.18571781203.
- ^ Giordano, Nicholas J. (2009). College physics: reasoning and relationships. Cengage Learning. hlm. 787. ISBN 0-534-42471-6. Extract of page 787
- ^ Bergmann, Peter Gabriel (1992). The riddle of gravitation. Courier Dover Publications. hlm. 17. ISBN 0-486-27378-4. Extract of page 17
- ^ Bais, Sander (2005). The equations: icons of knowledge. Harvard University Press. hlm. 40. ISBN 0-674-01967-9. Extract of page 40
- ^ O'Connor, JJ; Robertson, EF (November 1997). "James Clerk Maxwell". School of Mathematics and Statistics, Universitas St Andrews. Diarsipkan dari versi asli tanggal 2011-01-28. Diakses tanggal 2010-10-13.
- ^ Michelson, AA; Morley, EW (1887). "On the Relative Motion of the Earth and the Luminiferous Ether". American Journal of Science. 34: 333–345. doi:10.2475/ajs.s3-34.203.333.
- ^ French, AP (1983). Special relativity. Van Nostrand Reinhold. hlm. 51–57. ISBN 0-442-30782-9.
- ^ Darrigol, O (2000). Electrodynamics from Ampére to Einstein. Clarendon Press. ISBN 0-19-850594-9.
- ^ Galison, P (2003). Einstein's Clocks, Poincaré's Maps: Empires of Time. W.W. Norton. ISBN 0-393-32604-7.
- ^ Miller, AI (1981). Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911). Addison–Wesley. ISBN 0-201-04679-2.
- ^ Pais, A (1982). Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press. ISBN 0-19-520438-7.
- ^ "Resolution 6 of the 15th CGPM". BIPM. 1967. Diakses tanggal 2010-10-13.
- ^ Barger, R.; Hall, J. (1973). "Wavelength of the 3.39-μm laser-saturated absorption line of methane". Applied Physics Letters. 22 (4): 196. Bibcode:1973ApPhL..22..196B. doi:10.1063/1.1654608.
- ^ "Resolution 2 of the 15th CGPM". BIPM. 1975. Diakses tanggal 2009-09-09.
- ^ Taylor, EF; Wheeler, JA (1992). Spacetime Physics: Introduction to Special Relativity (edisi ke-2nd). Macmillan. ISBN 0-7167-2327-1.
- ^ Penzes, WB (2009). "Time Line for the Definition of the Meter" (PDF). NIST. Diakses tanggal 2010-01-11.
- ^
Adams, S (1997). Relativity: An Introduction to Space–Time Physics. CRC Press. hlm. 140. ISBN 0-7484-0621-2.
One peculiar consequence of this system of definitions is that any future refinement in our ability to measure c will not change the speed of light (which is a defined number), but will change the length of the meter!
- ^
Rindler, W (2006). Relativity: Special, General, and Cosmological (edisi ke-2nd). Oxford University Press. hlm. 41. ISBN 0-19-856731-6.
Note that [...] improvements in experimental accuracy will modify the meter relative to atomic wavelengths, but not the value of the speed of light!
- ^ The "explicit-constant" formulation Diarsipkan 2014-08-11 di Wayback Machine., BIPM 2011
- ^ Lihat, sebagai contoh:
- Conover, Emily (2 November 2016). "Units of measure are getting a fundamental upgrade". Science News (dalam bahasa Inggris). Diakses tanggal 6 February 2022.
- Knotts, Sandra; Mohr, Peter J.; Phillips, William D. (January 2017). "An Introduction to the New SI". The Physics Teacher (dalam bahasa Inggris). 55 (1): 16–21. doi:10.1119/1.4972491. ISSN 0031-921X.
- "SI Redefinition". National Institute of Standards and Technology (dalam bahasa Inggris). 11 May 2018. Diakses tanggal 6 February 2022.
Bacaan lebih lanjut[sunting | sunting sumber]
Referensi bersejarah[sunting | sunting sumber]
- Rømer, O (1676). "Démonstration touchant le mouvement de la lumière trouvé par M. Römer de l'Academie Royale des Sciences". Journal des sçavans (dalam bahasa French): 223–36. Diarsipkan dari versi asli tanggal 2007-07-29. Diakses tanggal 2015-12-29.
- Diterjemahkan sebagai "A Demonstration concerning the Motion of Light". Philosophical Transactions of the Royal Society (136): 893–4. 1677. doi:10.1098/rstl.1677.0024. Diarsipkan dari versi asli tanggal 2007-07-29. Diakses tanggal 2015-12-29.
- Halley, E (1694). "Monsieur Cassini, his New and Exact Tables for the Eclipses of the First Satellite of Jupiter, reduced to the Julian Stile and Meridian of London". Philosophical Transactions of the Royal Society. 18 (214): 237–56. doi:10.1098/rstl.1694.0048.
- Fizeau, HL (1849). "Sur une expérience relative à la vitesse de propagation de la lumière" (PDF). Comptes rendus de l'Académie des sciences (dalam bahasa French). 29: 90–92, 132. Archived from the original on 2011-06-13. Diakses tanggal 2015-12-29.
- Foucault, JL (1862). "Détermination expérimentale de la vitesse de la lumière: parallaxe du Soleil". Comptes rendus de l'Académie des sciences (dalam bahasa French). 55: 501–503, 792–796.
- Michelson, AA (1878). "Experimental Determination of the Velocity of Light". Proceedings of the American Association of Advanced Science. 27: 71–77.
- Michelson, AA; Pease, FG; Pearson, F (1935). "Measurement of the Velocity of Light in a Partial Vacuum". Astrophysical Journal. 82: 26–61. Bibcode:1935ApJ....82...26M. doi:10.1086/143655.
- Newcomb, S (1886). "The Velocity of Light". Nature. 34 (863): 29–32. Bibcode:1886Natur..34...29.. doi:10.1038/034029c0.
- Perrotin, J (1900). "Sur la vitesse de la lumière". Comptes rendus de l'Académie des sciences (dalam bahasa French). 131: 731–4.
Referensi modern[sunting | sunting sumber]
- Brillouin, L (1960). Wave propagation and group velocity. Academic Press.
- Jackson, JD (1975). Classical Electrodynamics (edisi ke-2nd). John Wiley & Sons. ISBN 0-471-30932-X.
- Keiser, G (2000). Optical Fiber Communications (edisi ke-3rd). McGraw-Hill. hlm. 32. ISBN 0-07-232101-6.
- Ng, YJ (2004). "Quantum Foam and Quantum Gravity Phenomenology". Dalam Amelino-Camelia, G; Kowalski-Glikman, J. Planck Scale Effects in Astrophysics and Cosmology. Springer. hlm. 321ff. ISBN 3-540-25263-0.
- Helmcke, J; Riehle, F (2001). "Physics behind the definition of the meter". Dalam Quinn, TJ; Leschiutta, S; Tavella, P. Recent advances in metrology and fundamental constants. IOS Press. hlm. 453. ISBN 1-58603-167-8.
- Duff, MJ (2004). "Comment on time-variation of fundamental constants". arΧiv:hep-th/0208093 [hep-th].
Pranala luar[sunting | sunting sumber]
- "Test Light Speed in Mile Long Vacuum Tube." Popular Science Monthly, September 1930, hlm. 17–18.
- Definisi meter (Biro Internasional untuk Ukuran dan Timbangan, BIPM)
- Laju cahaya dalam vakum (National Institute of Standards and Technology, NIST)
- Data Gallery: Michelson Speed of Light (Univariate Location Estimation) (data unduhan dikumpulkan oleh Albert A. Michelson)
- Subluminal (Applet Java yang mendemonstrasikan batas informasi kecepatan kelompok)
- De Mora Luminis di MathPages
- Diskusi ringan mengenai penambahan kecepatan
- c: Speed of Light (Sixty Symbols, University of Nottingham Department of Physics [video])
- FAQ Fisika Usenet
- Ilustrasi laju cahaya (Laju cahaya sebagai Live-Counter)

