Nilai dan vektor eigen

Dalam aljabar linear, vektor eigen (eigenvector) atau vektor karakteristik dari suatu matriks berukuran adalah vektor tak nol yang hanya mengalami perubahan panjang ketika dikali dengan matriks tersebut. Nilai eigen (eigenvalue) yang berasosiasi dengan vektor tersebut, umumnya dilambangkan dengan , menyatakan besar perubahan panjang vektor yang terjadi. Secara umum dalam ruang vektor multidimensi, vektor eigen tidak mengalami rotasi ketika ditransformasikan oleh matriks. Hal ini berlaku untuk matriks dengan elemen bilangan real, dan akan mengalami rotasi ketika elemen berupa bilangan kompleks.[1][2] Nilai eigen dan vektor eigen berguna dalam proses kalkulasi matriks, yang keduanya diterapkan dalam bidang matematika murni dan matematika terapan, contohnya pada transformasi linear.[3] Ruang eigen dari merupakan ruang vektor yang dibentuk dari gabungan vektor nol dan kumpulan vektor eigen yang berasosiasi dengan .[4]
Istilah eigen sering kali dipadankan dengan istilah karakteristik, karena kata "eigen" yang berasal dari bahasa Jerman memiliki arti "asli", dalam konteks menjadi ciri khas atau karakteristik dari suatu sifat.[5]
Pendahuluan[sunting | sunting sumber]
Nilai eigen dan vektor eigen umum ditemukan ketika melakukan analisis mengenai pemetaan (transformasi) linear. Istilah "eigen" yang berasal dari bahasa Jerman memiliki arti "asli", dalam konteks menjadi ciri khas atau karakteristik dari suatu sifat.[5] Awalnya konsep ini digunakan untuk mempelajari sumbu utama (principal axes) dari gerakan rotasi pada benda tegar. Nilai eigen dan vektor eigen saat ini telah diterapkan dalam banyak bidang, sebagai contoh dalam teori stabilitas, analisis getaran, orbital atom, pengenalan wajah (facial recognition), dan diagonalisasi matriks.
Pada dasarnya, suatu vektor eigen dari pemetaan linear adalah suatu vektor tak nol yang tidak berubah arah, ketika diterapkan oleh . Menerapkan ke vektor eigen hanya mengubah ukuran eigen vektor sebesar , yang disebut dengan nilai eigen. Kondisi ini dapat ditulis dalam bentuk persamaan sebagai

Lukisan Mona Lisa berikut menyajikan ilustrasi sederhana mengenai hal ini. Setiap titik pada lukisan dapat direpresentasikan sebagai sebuah vektor yang berasal dari pusat lukisan ke titik tersebut. Pemetaan linear dalam contoh ini disebut transformasi peregangan/pergeseran (shear mapping). Titik-titik yang berada di atas akan bergeser ke kanan, dan titik-titik di bawah akan bergeser ke kiri; sebanding dengan seberapa jauh posisi mereka dari sumbu horizontal yang terletak di tengah lukisan. Sebagai akibatnya, setiap vektor akan miring ke kanan atau ke kiri, dan menjadi semakin panjang atau semakin pendek. Namun, titik-titik yang terletak di sumbu horizontal tidak bergeser (miring) sama sekali. Alhasil, semua vektor yang mengarah ke kiri atau ke kanan, tanpa memiliki komponen vertikal, adalah vektor eigen dari pemetaan ini; karena pemetaan tersebut tidak mengubah arah vektor. Lebih lanjut, vektor-vektor eigen ini memiliki nilai eigen sebesar 1, karena pemetaan juga tidak mengubah ukuran mereka.
Pemetaan linear dapat muncul dalam banyak bentuk dan memetakan banyak jenis ruang vektor, sehingga vektor eigen dapat memiliki rupa yang bermacam-macam. Sebagai contoh, pemetaan linear dapat berbentuk operator turunan seperti , dan vektor eigen disebut sebagai fungsi eigen (eigenfunctions) yang mengalami penskalaan oleh operator tersebut; contohnya fungsi
Nilai eigen dan vektor eigen menghasilkan banyak konsep matematika yang berhubungan, dan istilah "eigen" ditambahkan ketika menamai mereka:
- Himpunan vektor eigen dari pemetaan linear, masing-masing dipasangkan dengan nilai eigen mereka, disebut dengan sistem eigen (eigensystem) dari transformasi tersebut.[6][7]
- Himpunan dari semua vektor eigen dari yang berasosiasi dengan suatu nilai eigen, dan ditambah dengan vekotr nol, disebut dengan ruang eigen (eigenspace) atau ruang karakteristik dari yang berasosiasi dengan nilai eigen tersebut.[8]
- Jika suatu himpunan vektor eigen dari membentuk sebuah basis bagi domain dari , maka basis ini disebut basis eigen (eigen basis).
Definisi formal[sunting | sunting sumber]
Jika adalah suatu pemetaan linear dari suatu ruang vektor atas lapangan ke dirinya sendiri, dan adalah vektor tak nol di , maka adalah vektor eigen dari jika adalah suatu kelipatan skalar dari . Hal ini dapat ditulis sebagai
dengan adalah suatu skalar di , yang disebut dengan nilai eigen (eigenvalue), nilai karakteristik, atau akar karakteristik, yang berasosiasi dengan .
Ada hubungan erat antara matriks persegi berukuran dengan pemetaan linear dari ruang vektor berdimensi ke dirinya sendiri. Hal ini menyebabkan, dalam suatu ruang vektor berdimensi hingga, nilai eigen dan vektor eigen dapat didefinisikan menggunakan bahasa matriks, maupun menggunakan bahasa pemetaan linear.[9][10] Jika berdimensi hingga, persamaan di atas setara dengan[11]
dengan adalah representasi matriks dari dan adalah vektor koordinat dari .
Nilai dan vektor eigen dari matriks[sunting | sunting sumber]

Nilai eigen dan vektor eigen sering diperkenalkan ke murid dalam konteks kelas aljabar linear yang berfokus pada matriks.[12][13] Lebih lanjut, pemetaan linear atas ruang vektor hingga dapat dinyatakan menggunakan matriks,[9][10] yang umum digunakan secara numerik maupun komputasi.[14] Misalkan vektor berdimensi yang dibentuk sebagai barisan buah skalar; contohnya vektor berdimensi 3
-
(1)
maka adalah vektor eigen dari pemetaan linear dan skalar adalah nilai eigen yang berasosiasi dengan vektor eigen tersebut. Persamaan (1) adalah persamaan nilai eigen untuk matriks . Persamaan (1) juga dapat dinyatakan sebagai
-
(2)
dengan adalah matriks identitas dan adalah vektor nol.
Nilai eigen dan polinomial karakteristik[sunting | sunting sumber]
Persamaan (2) memiliki solusi tak nol jika dan hanya jika nilai determinan dari matriks adalah nol. Dengan demikian, nilai-nilai eigen dari adalah nilai-nilai yang memenuhi persamaan
-
(3 )
Dengan menggunakan rumus Leibniz, ruas kiri pada Persamaan (3) dapat dijabarkan menjadi sebuah fungsi polinomial dengan variabel dan berderajat , yakni ukuran dari matriks . Koefisien-koefisien polinom ini bergantung pada entri-entri matriks , kecuali suku berderajat yang akan memiliki koefisien . Polinomial ini disebut sebagai polinomial karakteristik dari . Persamaan (3) sendiri disebut sebagai persamaan karakteristik dari .[1][15] Teorema dasar aljabar mengakibatkan polinomial karakteristik dari , yang berderajat , dapat difaktorkan sebagai perkalian buah suku linear,
-
(4 )
dengan setiap dapat berupa bilangan real, walau pada umumnya berupa kompleks. Nilai , yang mungkin tidak semuanya unik, adalah akar-akar dari polinomial dan merupakan nilai eigen dari .
Sebagai contoh singkat, yang akan dijelaskan pada bagian Contoh nanti, misalkan sebuah matriks
Dengan menghitung determinan dari , didapatkan polinom karakteristik dari yakni
Setelah mencari akar dari polinom ketika sama dengan nol, didapatkan akar dan , yang selanjutnya merupakan nilai eigen dari . Vektor eigen yang berasosiasi dengan masing-masing nilai eigen tersebut dapat ditentukan dengan menyelesaikan komponen di persamaan . Dalam contoh ini, vektor eigen adalah sembarang kelipatan skalar (tak nol) dari
Bagian imajiner dari akar pada polinomial real dengan koefisien-koefisien real dapat dikelompokkan dalam pasangan konjugat kompleks, yakni dengan anggotanya memiliki bagian real yang sama dan hanya berbeda tanda di bagian imajinernya. Jika polinom berderajat ganjil, maka teorema nilai antara mengatakan setidaknya satu akar akan berupa real. Dengan demikian, sembarang matriks real berukuran ganjil akan memiliki setidaknya satu nilai eigen real, sedangkan matriks real berukuran genap mungkin tidak memiliki satupun nilai eigen real. Vektor-vektor eigen yang berasosiasi dengan nilai-nilai eigen kompleks akan memiliki komponen kompleks, dan juga muncul dalam pasangan konjugat kompleks.
Kegandaan aljabar[sunting | sunting sumber]
Misalkan adalah nilai eigen dari suatu matriks berukuran . Kegandaan aljabar[16] (algebraic multiplicity) menyatakan bilangan terbesar yang membuat dapat membagi habis polinomial karakteristik dari .[8][17][18]
Jika berdimensi dan memiliki nilai eigen yang berbeda, Persamaan (4) dapat dinyatakan secara lebih ringkas sebagai
Ruang eigen, kegandaan geometrik, dan basis eigen bagi matriks[sunting | sunting sumber]
Misalkan adalah suatu nilai eigen dari matriks berukuran , dan himpunan berisi semua vektor yang memenuhi Persamaan (2),
Di satu sisi, himpunan ini adalah kernel atau ruang nol (nullspace) dari matriks . Di sisi lain, dari definisi, setiap vektor tak nol yang memenuhi Persamaan (2) adalah vektor-vektor eigen dari yang berasosiasi dengan . Jadi, himpunan adalah gabungan vektor nol dengan himpunan semua vektor eigen dari yang berasosiasi dengan , sekaligus sama dengan kernel dari . Himpunan disebut sebagai ruang eigen (eigenspace) dari yang berasosiasi dengan .[8][19] Secara umum akan berupa bilangan kompleks dan vektor eigen akan berupa matriks kompleks berukuran .
Ruang eigen tertutup atas penjumlahan, karena is adalah suatu subruang vektor (dari ). Dengan kata lain, untuk sembarang vektor dan anggota , vektor juga anggota ; atau secara ekuivalen, . Hal ini dapat dibuktikan dengan menggunakan sifat distributif perkalian matriks. Serupa dengan itu, juga tertutup atas perkalian skalar. Artinya, jika dan merupakan bilangan kompleks, maka ; atau secara ekuivalen, . Hal ini dapat dibuktikan dengan menggunakan sifat komutatif perkalian matriks kompleks dengan bilangan kompleks. Selama dan bukan vektor nol, mereka juga merupakan vektor eigen dari yang berasosiasi dengan .
Dimensi dari ruang eigen yang berasosiasi dengan , yakni banyaknya vektor eigen yang berasosiasi dengan dan saling bebas linear, disebut dengan kegandaan geometrik (geometric multiplicity) dari nilai eigen , disimbolkan dengan . Karena sama dengan kernel dari , maka kegandaan geometrik dari adalah dimensi dari kernel , juga disebut sebagai nolitas dari , dan berhubungan dengan dimensi dan rank dari lewat persamaan
Sebagai akibat dari definisi nilai eigen dan vektor eigen, nilai kegandaan numerik dari suatu nilai eigen setidaknya sama dengan 1. Lebih lanjut, nilai kegandaan numerik dari tidak dapat melebihi nilai kegandaan aljabarnya; dan kegandaan aljabar tidak dapat melebihi dimensi dari matriks . Secara matematis hal tersebut dapat ditulis sebagai
Untuk membuktikan pertidaksamaan , pertimbangkan bahwa definisi kegandaan geometrik mengakibatkan eksistensi buah vektor eigen yang ortonormal, dan memenuhi . Kita dapat menemukan matriks (uniter) yang kolom pertamanya adalah vektor-vektor eigen ini, dan kolom-kolom yang tersisa adalah sembarang himpunan buah vektor ortonormal yang ortogonal dengan vektor-vektor eigen tadi. Maka memiliki rank penuh sehingga memiliki invers, dan memenuhi persamaan , dengan adalah matriks yang blok bagian atas kirinya adalah matriks diagonal . Hal ini mengimplikasikan . Dengan kata lain, serupa dengan , yang selanjutnya mengakibatkan . Namun dari definisi matriks kita ketahui bahwa mengandung faktor , yang mengartikan kegandaan aljabar dari harus memenuhi .
Misalkan memiliki nilai eigen unik , dengan kegandaan geometrik dari adalah . Total kegandaan geometrik dari ,
adalah dimensi dari jumlah semua ruang eigen dari nilai-nilai eigen ; atau secara ekuivalen, adalah banyaknya vektor-vektor eigen dari yang saling bebas linear. Jika , maka
- Jumlah langsung semua ruang eigen dari nilai-nilai eigen akan sama dengan ruang vektor .
- Suatu basis bagi dapat dibentuk dari buah eigen vektor dari yang saling bebas linear; basis tersebut dikatakan sebagai basis eigen (eigenbasis)
- Sembarang vektor di dapat dinyatakan sebagai kombinasi linear dari vektor-vektor eigen dari .
Sifat-sifat lain dari nilai eigen[sunting | sunting sumber]
Misalkan adalah sembarang matriks berukuran dengan entri berupa bilangan kompleks, dan memiliki nilai-nilai eigen . Setiap nilai eigen muncul sebanyak kali di polinomial karakteristik matriks , dengan menyatakan kegandaan numerik dari nilai eigen. Berikut beberapa hubungan yang dimiliki matriks dengan nilai-nilai eigennya:
- Trace dari , yang didefinisikan sebagai jumlah elemen-elemen diagonal utama pada matriks, bernilai sama dengan jumlah semua nilai eigen matriks tersebut,[20][21][22]
- Determinan dari adalah hasil perkalian semua nilai eigen matriks tersebut,[20][22][23]
- Nilai-nilai eigen dari matriks , untuk sembarang bilangan bulat positif , adalah .
- Matriks dapat dibalik (memiliki invers) jika dan hanya jika tidak ada nilai eigennya yang bernilai nol.
- Jika terbalikkan, maka nilai-nilai eigen dari adalah . Lebih lanjut, nilai eigen dari dan nilai eigen dari akan memiliki nilai kegandaan geometrik dan kegandaan aljabar yang sama.
- Jika sama dengan transpos konjugat dirinya, , dengan kata lain merupakan matriks Hermite, maka semua nilai eigennya bernilai real. Hal yang sama berlaku untuk sembarang matriks simetrik real.
- Jika merupakan matriks Hermite sekaligus bersifat definit positif, semidefinit positif, definit negatif, atau semidefinit negatif; maka berturut-turut, setiap nilai eigennya akan berupa bilangan positif, tak negatif, negatif, atau tak positif.
- Jika uniter, setiap nilei eigennya memiliki nilai mutlak .
- Nilai-nilai eigen dari matriks (dengan adalah matriks identitas) adalah . Lebih lanjut, jika , nilai-nilai eigen dari adalah . Secara umum untuk sembarang polinomial , nilai-nilai eigen dari matriks adalah .
Identitas nilai dan vektor eigen[sunting | sunting sumber]
Untuk sembarang matriks Hermite, kuadrat norma dari komponen ke- dari vektor eigen yang ternormalisasi dapat ditentukan hanya dengan menggunakan nilai-nilai eigen dari matriks dan nilai-nilai matriks minor yang bersesuaian,
dengan adalah submatriks yang dibentuk dengan menghilangkan baris dan kolom ke- dari matriks awalnya.[24][25][26]
Contoh perhitungan nilai eigen dan vektor eigen[sunting | sunting sumber]
Contoh matriks dimensi dua[sunting | sunting sumber]

Misalkan sebuah matriks
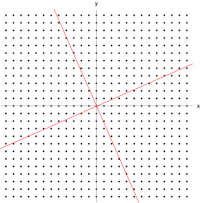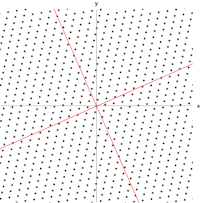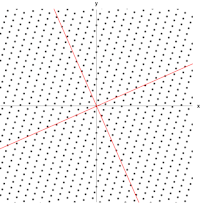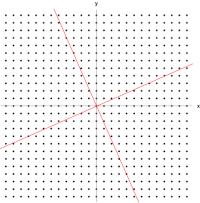
Gambar berikut menunjukkan efek dari transformasi oleh matriks pada titik-titik koordinat yang terletak pada bidang. Vektor-vektor eigen dari transformasi ini memenuhi Persamaan (1), dan nilai-nilai eigennya adalah nilai-nilai yang menyebabkan determinan matriks sama dengan nol. Dengan menghitung determinan, kita mendapatkan polinomial karakteristik dari ,
Polinom karakteristik ini memiliki akar dan , yang selanjutnya adalah dua nilai eigen dari . Mensubtitusi ke dalam Persamaan (2), didapatkan
- ;
Sembarang vektor tak nol dengan akan memenuhi persamaan ini. Dengan demikian, dapat dipilih satu vektor,
sebagai vektor eigen dari yang berasosiasi dengan ; setiap kelipatan dari vektor ini juga merupakan vektor eigen. Sedangkan untuk , Persamaan (2) dapat ditulis menjadi
Sembarang vektor tak nol dengan akan memenuhi persamaan ini. Dengan cara yang sama seperti di atas,
adalah vektor eigen dari yang berasosiasi dengan . Alhasil, vektor dan adalah vektor eigen dari , yang masing-masing berasosiasi dengan dan .
Rumus umum untuk nilai-nilai eigen dari matriks dimensi dua[sunting | sunting sumber]
Nilai-nilai eigen dari matriks real adalah[a]
Dengan adalah operator trace. Nilai-nilai eigen akan selalu berupa bilangan real ketika dan memiliki tanda yang sama, karena nilai di dalam akar tidak akan bernilai negatif
Contoh matriks dimensi tiga[sunting | sunting sumber]
Misalkan sebuah matriks dengan nilai entri-entri berikut,[27]
Pertama-tama akan dihitung polinomial karakteristik dari matriks dengan menghitung ekspansi Laplace dari matriks
Persamaan karakteristik memiliki akar-akar . Untuk , subtitusi nilai eigen ke dalam Persamaan (2) akan menghasilkan
Contoh matriks dimensi tiga dengan nilai-nilai eigen kompleks[sunting | sunting sumber]
Misalkan sebuah matriks permutasi
Matriks ini akan menggeser koordinat vektor ke atas sebesar satu posisi, dan memindahkan koordinat pertama menjadi koordinat terakhir. Polinomial karakteristik matriks ini adalah , yang memiliki akar-akar
dengan adalah unit imajiner yang memiliki sifat . Untuk nilai eigen real , sembarang vektor dengan semua entrinya bernilai sama adalah vektor eigen. Sebagai contoh,
Sedangkan untuk dua nilai eigen lainnya, yang merupakan pasangan bilangan kompleks konjugat, akan memenuhi hubungan
Contoh matriks diagonal[sunting | sunting sumber]
Matriks dengan entri-entri tak nol hanya terletak sepanjang diagonal utama disebut dengan matriks diagonal. Nilai-nilai eigen dari matriks diagonal adalah nilai-nilai sepanjang diagonal utama matriks itu sendiri. Sebagai contoh, misalkan sebuah matriks
Contoh matriks segitiga[sunting | sunting sumber]
Suatu matriks dengan semua entri di atas diagonal utama bernilai nol disebut dengan matriks segitiga bawah, sedangkan matriks dengan semua entri di bawah diagonal utama bernilai nol disebut dengan matriks segitiga atas. Sama seperti matriks diagonal, nilai-nilai eigen dari matriks segitiga terletak pada diagonal utama. Sebagai contoh, misalkan sebuah matriks segitiga bawah,
Contoh matriks dengan nilai eigen yang berulang[sunting | sunting sumber]
Serupa dengan contoh sebelumnya, matriks segitiga bawah
Sejarah[sunting | sunting sumber]
Nilai-nilai eigen umum diperkenalkan dalam konteks aljabar linear atau teori matriks. Namun secara historis, mereka muncul dalam studi mengenai bentuk kuadratik dan persamaan diferensial.
Pada abad ke-18, Leonhard Euler mempelajari gerakan rotasi dari benda tegar, dan menemukan pentingnya konsep poros utama (principal axes). Tepatnya tahun 1751, Leonhard Euler membuktikan bahwa setiap benda memiliki suatu poros rotasi utama (principal axis of rotation).[28] Hasil ini dikembangkan oleh Johann Andreas Segner, yang pada tahun 1755 membuktikan setiap benda memiliki tiga poros rotasi utama.[29][30] Joseph-Louis Lagrange selanjutnya menyadari bahwa poros-poros utama adalah vektor-vektor eigen dari matriks inersia.[31]
Pada awal abad ke-19, Augustin Louis Cauchy melihat bagaimana karya-karya mereka dapat digunakan untuk mengklasifikasi kurva kuadratik (quadric surfaces), lalu memperumumnya ke sembarang dimensi.[31] Karya tulis Cauchy juga berpengaruh terhadap perkembangan teori spektral pada awal tahun 1870.[31] Cauchy juga mencetuskan istilah racine caractéristique (akar karakteristik), yang sekarang disebut sebagai nilai eigen; istilah lain yang ia cetuskan dan masih bertahan saat ini adalah persamaan karakteristik.[32][33] Selanjutnya, Joseph Fourier menggunakan karya Lagrange dan Pierre-Simon Laplace untuk menyelesaikan persamaan panas dengan pemisahan variabel, dalam buku tahun 1822-nya yang terkenal, Théorie analytique de la chaleu (Teori analitik tentang panas).[34] Charles-François Sturm mengembangkan ide Fourier lebih jauh, dan menarik perhatian Cauchy, yang menggabungkan ide-ide mereka dengan idenya sendiri, dan menghasilkan bukti bahwa matriks simetrik real akan memiliki nilai-nilai eigen real.[31] Hasil ini diperumum oleh Charles Hermite pada tahun 1855, yang memperkenalkan matriks Hermite.[32]
Di saat yang bersamaan, Francesco Brioschi membuktikan nilai-nilai eigen dari matriks ortogonal terletak pada lingkaran satuan,[31] dan Alfred Clebsch menemukan bukti yang serupa untuk matriks skew-symmetric.[32] Karl Weierstrass mengklarifikasi aspek penting dalam teori stabilitas yang dibuat oleh Laplace, dengan membuktikan matriks defektif dapat menyebabkan ketidakstabilan.[31] Joseph Liouville mempelajari masalah-masalah nilai eigen yang mirip dengan masalah yang dikerjakan Sturm; menghasilkan disiplin ilmu yang saat ini dikenal dengan teori Sturm-Liouville.[35] Memasuki akhir abad ke-19, Schwarz mempelajari nilai eigen pertama dari persamaan Laplace secara umum, sedangkan Poincaré mempelajari persamaan Poisson beberapa tahun berikutnya.[36]
Di awal abad ke-20, David Hilbert mempelajari nilai-nilai eigen dari operator integral dengan menganggap operator tersebut sebagai matriks [dengan ukuran] tak berhingga.[37] Ia adalah yang pertama menggunakan kata German eigen, yang berarti "diri sendiri"[38] untuk menyebut nilai dan vektor eigen pada tahun 1904,[39][40] walau ada kemungkinan ia mengikuti istilah yang digunakan oleh Hermann von Helmholtz. Untuk beberapa waktu, istilah yang digunakan dalam bahasa Inggris adalah "proper value" (nilai yang tepat), namun istilah "eigenvalue" menjadi standar saat ini.[40] Sedangkan dalam Bahasa Indonesia, Pusat Bahasa memadankan istilah "eigenvalue" istilah "eigennilai"[41]. Namun saat ini, istilah "nilai eigen" lebih populer digunakan.[butuh rujukan]
Algoritma numerik pertama untuk menghitung nilai-nilai eigen dan vektor-vektor eigen muncul pada tahun 1929, saat Richard von Mises mempublikasikan metode pangkat. Salah satu metode yang populer saat ini adalah algoritma QR, yang diusulkan secara terpisah oleh John G. F. Francis[42][43] dan Vera Kublanovskaya[44] pada tahun 1961.[45][46]
Metode penyelesaian[sunting | sunting sumber]
Teori tentang cara menentukan nilai dan vektor eigen, seperti yang disajikan dalam buku-buku aljabar linear dasar, umumnya tidak digunakan dalam praktiknya.
Metode klasik[sunting | sunting sumber]
Metode klasik bekerja dengan mencari nilai-nilai eigen terlebih dahulu, lalu menentukan vektor-vektor eigen untuk setiap nilai eigen. Dalam beberapa cara metode ini tidak sesuai untuk aritmetika non-eksak (non-exact arithmetics) seperti floating-point.
Nilai-nilai eigen dari suatu matriks dapat ditentukan dengan mencari akar-akar polinomial karakteristik. Hal ini sederhana untuk matriks berukuran , namun kesulitan akan meningkat dengan sangat cepat sebanding dengan ukuran matriks. Dalam teori, koefisien-koefisien dari polinomial karakteristik dapat dihitung secara eksak karena mereka adalah hasil penjumlahan dari perkalian elemen-elemen matriks; lagipula ada beberapa algoritma yang dapat mencari akar-akar dari polinomial dengan sembarang derajat akurasi yang diinginkan.[47] Namun cara tidak dapat dilakukan dalam praktik karena koefisien-koefisien akan terkontaminasi dengan galat pembulatan, sedangkan akar-akar polinomial dapat sangat sensitif terhadap perubahan koefisien-koefisien (seperti yang dicontohkan pada polinomial Wilkinson).[47] Bahkan untuk matriks yang setiap entrinya berupa bilangan bulat, kalkulasi tetap membutuhkan banyak operasi penjumlahan.
Rumus aljabar untuk mencari akar-akar polinomial secara eksplisit hanya ada jika derajat polinomial . Berdasarkan teorema Abel-Ruffini, tidak ada rumus aljabar eksak yang eksplisit, untuk mencari akar-akar polinomial derajat 5 atau lebih. Hal ini menyebabkan nilai dan vektor eigen dari matriks berorde 5 atau lebih, perlu dicari sebagai hampiran/perkiraan dengan metode numerik. Bahkan rumus eksplisit untuk akar-akar polinomial derajat 3 sudah tidak praktis secara numerik.
Setelah nilai (eksak) dari nilai eigen diketahui, vektor-vektor yang berasosiasi dengannya dapat dicari dengan mencari solusi tak nol dari persamaan nilai eigen; dengan kata lain, menyelesaikan sebuah sistem persamaan linear.
Metode iteratif sederhana[sunting | sunting sumber]
Pendekatan sebaliknya, yakni dengan mencari vektor-vektor eigen lalu menentukan nilai eigen yang berasosiasi dengannya, ternyata lebih mudah dikerjakan oleh komputer. Algoritma yang paling sederhana dilakukan dengan mengambil sembarang vektor awal, lalu secara berulang mengalikannya dengan matriks (dan secara opsional juga melakukan normalisasi agar ukuran vektor tetap wajar); hal ini akan membuat vektor menghampiri suatu vektor eigen. Iterasi invers sebagai salah satu variasi, mengalikan vektor dengan matriks ; hal ini menyebabkan vektor untuk menghampiri vektor eigen dengan nilai eigen yang nilainya sedekat mungkin dengan .
Jika adalah (perkiraan hampiran yang bagus dari) sebuah vektor eigen dari , maka nilai eigen yang berasosiasi dengan vektor tersebut dihitung lewat
Metode modern[sunting | sunting sumber]
Metode yang efisien dan akurat untuk menghitung nilai dan vektor eigen dari sembarang matriks tidak diketahui, sampai saat algoritma QR berhasil dikembangkan pada tahun 1961.[47] Algoritma dengan menggabungkan transformasi Householder dengan dekomposisi LU menghasilkan hampiran yang lebih baik ketimbang algoritma QR.[butuh rujukan] Untuk matriks Hermite yang rongga, algoritma Lanczos adalah salah satu contoh metode iteratif yang efisien untuk menghitung nilai dan vektor eigen.[47]
Banyak metode numerik yang menghitung nilai-nilai eigen dari matriks juga menghasilkan vektor-vektor eigen sebagai produk sampingan, tapi terkadang hal ini tidak dibutuhkan pada masalah yang dikerjakan, sehingga informasi vektor-vektor eigen ini langsung dibuang.
Catatan kaki[sunting | sunting sumber]
- ^
Tentukan polinomial karakteristik dari :
Lalu gunakan rumus kuadratik untuk menentukan nilai dari :Bentuk di dalam akar dapat diserdehanakan menjadi:Dengan sedikit perapian,
Referensi[sunting | sunting sumber]
- ^ a b Kuttler, Kenneth (2012-01-10). Elementary Linear Algebra (dalam bahasa Inggris). The Saylor Foundation.
- ^ Kuttler, Kenneth. 2012. Linear Algebra II: Spectral Theory and Abstract Vector Spaces. Ventus Publishing ApS. ISBN 978-87-403-0241-7
- ^ Leon, Steven J. . 2001 . Aljabar Linear dan Aplikasinya, Edisi Kelima . Jakarta: Erlangga . ISBN 979-688-173-X
- ^ Weisstein, Eric W. "Eigenspace". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2021-11-11.
- ^ a b Axler, Sheldon . 1997 . ‘’’Linear Algebra Done Right Second Edition’’’ . Springer-Verlag New York, Inc. . ISBN 0-387-98259-0
- ^ Press, William H. (2007). Numerical recipes : the art of scientific computing. Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery, Cambridge University Press (edisi ke-3rd ed). Cambridge, UK. hlm. 536. ISBN 978-0-521-88407-5. OCLC 123285342.
- ^ Weisstein, Eric W. "Eigenvector". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2021-11-11.
- ^ a b c Nering, Evar D. (1970). Linear algebra and matrix theory (edisi ke-2d ed). New York: Wiley. hlm. 107. ISBN 978-0-471-63178-1.
- ^ a b Herstein, Israel N. (1964). Topics in algebra. Waltham, Mass: Xerox College Publ. hlm. 228–229. ISBN 0-536-00257-6. OCLC 615439706.
- ^ a b Nering, Evar D. (1970). Linear algebra and matrix theory (edisi ke-2d ed). New York,: Wiley. hlm. 38. ISBN 0-471-63178-7. OCLC 747523.
- ^ Weisstein, Eric W. "Eigenvalue". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2020-08-19.
- ^ Cornell University Department of Mathematics (2016) Lower-Level Courses for Freshmen and Sophomores. Accessed on 2016-03-27.
- ^ University of Michigan Mathematics (2016) Math Course Catalogue Diarsipkan 2015-11-01 di Wayback Machine.. Accessed on 2016-03-27.
- ^ Press, William H. (2007). Numerical recipes : the art of scientific computing. Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery, Cambridge University Press (edisi ke-3rd ed). Cambridge, UK. hlm. 38. ISBN 978-0-521-88407-5. OCLC 123285342.
- ^ Matthews, K. R. (2013). Elementary Linear Algebra (PDF). Department of Mathematics, University of Queensland.
- ^ "Glosarium". bahasasastra.kemdikbud.go.id. Diakses tanggal 2021-11-12.
- ^ Fraleigh, John B. (1976). A first course in abstract algebra (edisi ke-2d ed). Reading, Mass.: Addison-Wesley Pub. Co. hlm. 358. ISBN 0-201-01984-1. OCLC 2344185.
- ^ a b Golub, Gene H. (1996). Matrix computations. Charles F. Van Loan (edisi ke-3rd ed). Baltimore: Johns Hopkins University Press. hlm. 316. ISBN 0-8018-5413-X. OCLC 34515797.
- ^ Anton, Howard (1987). Elementary linear algebra (edisi ke-5th ed). New York: Wiley. hlm. 305–307. ISBN 0-471-84819-0. OCLC 13580207.
- ^ a b Beauregard, Raymond A. (1973). A first course in linear algebra; with optional introduction to groups, rings, and fields. John B. Fraleigh. Boston,: Houghton Mifflin. hlm. 307. ISBN 0-395-14017-X. OCLC 600254.
- ^ Herstein, Israel N. (1964). Topics in algebra. Waltham, Mass: Xerox College Publ. hlm. 272. ISBN 0-536-00257-6. OCLC 615439706.
- ^ a b Nering, Evar D. (1970). Linear algebra and matrix theory (edisi ke-2d ed). New York,: Wiley. hlm. 115–116. ISBN 0-471-63178-7. OCLC 747523.
- ^ Herstein, Israel N. (1964). Topics in algebra. Waltham, Mass: Xerox College Publ. hlm. 290. ISBN 0-536-00257-6. OCLC 615439706.
- ^ Denton, Peter B.; Parke, Stephen J.; Tao, Terence; Zhang, Xining (2021-02-18). "Eigenvectors from eigenvalues: A survey of a basic identity in linear algebra". Bulletin of the American Mathematical Society: 1. doi:10.1090/bull/1722. ISSN 0273-0979.
- ^ Wolchover, Natalie (2019-11-13). "Neutrinos Lead to Unexpected Discovery in Basic Math". Quanta Magazine (dalam bahasa Inggris). Diakses tanggal 2021-11-12.
- ^ Van Mieghem, Piet (2016-03-14). "Graph eigenvectors, fundamental weights and centrality metrics for nodes in networks". arXiv:1401.4580 [cond-mat, physics:physics].
- ^ Anton H., & Rorres C. 2005 . Elementary Linear Algebra: 9th edition . John Wiley and Sons. New York . ISBN 0-471-43329-2
- ^ Euler, Leonhard (Oktober 1751). Du mouvement d'un corps solide quelconque lorsqu'il tourne autour d'un axe mobile [Tentang pergerakan benda tegar ketika berotasi mengelilingi suatu poros] (dalam bahasa Prancis). Oxford University. Histoire de l'Académie royale des sciences et des belles lettres de Berlin. (dipublikasikan tanggal tahun 1760). hlm. 176–227.
Pada hlm. 212, Euler membuktikan bahwa setiap benda memiliki suatu poros rotasi utama (principal axis of rotation). "Théorem. 44. De quelque figure que soit le corps, on y peut toujours assigner un tel axe, qui passe par son centre de gravité, autour duquel le corps peut tourner librement & d'un mouvement uniforme." (Teorema. 44. Bagaimanapun bentuk bendanya, seseorang dapat menetapkan suatu poros yang melewati titik pusat gravitasi [benda], sehingga benda tersebut dapat berputar bebas dan dengan gerakan yang seragam (konstan).)
- ^ Segner, Johann Andreas (1755). Specimen theoriae turbinum [Esai mengenai teori tentang gasing (yakni, benda yang berotasi)]. Halle (Halae), Jerman: Gebauer. hlm. xxviiii [29].
Segner menyusun persamaan derajat tiga dalam t, yang membuktikan sebuah benda memiliki tiga poros rotasi utama. Ia selanjutnya menyatakan (di halaman yang sama): "Non autem repugnat tres esse eiusmodi positiones plani HM, quia in aequatione cubica radices tres esse possunt, et tres tangentis t valores." (Namun, itu tidak inkonsisten bahwa ada tiga posisi tersebut di bidang HM, karena persamaan kubik dapat memiliki tiga akar, dan tiga nilai untuk tangen t.)
- ^ Cayley, A. (1863). "Report on the progress of the solution of certain special problems of dynamics" [Laporan mengenai perkembangan solusi dari beberapa masalah khusus dalam dinamika]. Report of the Thirty-second meeting of the British Association for the Advancement of Science. Cambridge (dipublikasikan tanggal October 1862). 32: 184–252.
Karya Segner didiskusikan secara singkat, khususnya pada hlm. 225-226
- ^ a b c d e f Hawkins, Thomas (1975-02-01). "Cauchy and the spectral theory of matrices". Historia Mathematica (dalam bahasa Inggris). 2 (1): 1–29. doi:10.1016/0315-0860(75)90032-4. ISSN 0315-0860.
- ^ a b c Kline, Morris (1972). Mathematical thought from ancient to modern times. New York. hlm. 807–808. ISBN 0-19-501496-0. OCLC 517172.
- ^ Cauchy, Augustin (1839). "Mémoire sur l'intégration des équations linéaires" [Memoir tentang integrasi persamaan linear]. Comptes rendus de l'Académie des Sciences. 8: 827–830, 845–865, 889–907, 931–937.
Di hlm. 827: "On sait d'ailleurs qu'en suivant la méthode de Lagrange, on obtient pour valeur générale de la variable prinicipale une fonction dans laquelle entrent avec la variable principale les racines d'une certaine équation que j'appellerai l'équation caractéristique, le degré de cette équation étant précisément l'order de l'équation différentielle qu'il s'agit d'intégrer." (Kita tahu, lebih lanjut, dengan menggunakan metode Lagrange, kita akan mendapatkan nilai umum dari variabel utama sebuah fungsi yang disana, bersama dengan variabel utama, akan dari suatu persamaan yang akan saya sebut sebagai "persamaan karakteristik", derajat dari persamaan ini dengan tepat sama dengan derajat dari persamaan diferensial yang perlu diintegrasikan.)
- ^ Kline, Morris (1972). Mathematical thought from ancient to modern times. New York. hlm. 673. ISBN 0-19-501496-0. OCLC 517172.
- ^ Kline, Morris (1972). Mathematical thought from ancient to modern times. New York. hlm. 715–716. ISBN 0-19-501496-0. OCLC 517172.
- ^ Kline, Morris (1972). Mathematical thought from ancient to modern times. New York. hlm. 706–707. ISBN 0-19-501496-0. OCLC 517172.
- ^ Kline, Morris (1972). Mathematical thought from ancient to modern times. New York. hlm. 1063. ISBN 0-19-501496-0. OCLC 517172.
- ^ "Eigenvector and Eigenvalue". www.mathsisfun.com. Diakses tanggal 2020-08-19.
- ^ Hilbert, David (1904). Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen. (Erste Mitteilung) [Fundamental mengenai teori umum tentang persamaan integral. (Laporan pertama)] (dalam bahasa Jerman). Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (News of the Philosophical Society at Göttingen, mathematical-physical section). hlm. 49–91.
Di hlm. 51: "Insbesondere in dieser ersten Mitteilung gelange ich zu Formeln, die die Entwickelung einer willkürlichen Funktion nach gewissen ausgezeichneten Funktionen, die ich 'Eigenfunktionen' nenne, liefern: …" (Secara khusus, dalam laporan pertama ini saya menemukan rumus yang memberikan perkembangan [deret?] dari sembarang fungsi yang dinyatakan dalam suatu fungsi yang khusus, yang saya sebut dengan nilai eigen: …) Selanjutnya dalam halaman yang sama: "Dieser Erfolg ist wesentlich durch den Umstand bedingt, daß ich nicht, wie es bisher geschah, in erster Linie auf den Beweis für die Existenz der Eigenwerte ausgehe, … " (Kesuksesan ini terutama disebabkan oleh bahwa saya tidak, sampai saat ini, pertama-tama berniat untuk membuktikan eksistensi dari nilai eigen, …)
- ^ a b Aldrich, John. Miller, Jeff, ed. "Earliest Known Uses of Some of the Words of Mathematics (E)". jeff560.tripod.com. Diakses tanggal 2021-11-12.
lihat bagian "EIGENVALUE, EIGENFUNCTION, EIGENVECTOR and related terms."
- ^ "Glosarium". bahasasastra.kemdikbud.go.id. Diakses tanggal 2021-11-12.
- ^ Francis, J. G. F. (1961-03-01). "The QR Transformation A Unitary Analogue to the LR Transformation--Part 1". The Computer Journal (dalam bahasa Inggris). 4 (3): 265–271. doi:10.1093/comjnl/4.3.265. ISSN 0010-4620.
- ^ Francis, J. G. F. (1962-04-01). "The QR Transformation--Part 2". The Computer Journal (dalam bahasa Inggris). 4 (4): 332–345. doi:10.1093/comjnl/4.4.332. ISSN 0010-4620.
- ^ Kublanovskaya, V.N. (1962-01). "On some algorithms for the solution of the complete eigenvalue problem". USSR Computational Mathematics and Mathematical Physics (dalam bahasa Inggris). 1 (3): 637–657. doi:10.1016/0041-5553(63)90168-X.
- ^ Golub, Gene H. (1996). Matrix computations. Charles F. Van Loan (edisi ke-3rd ed). Baltimore: Johns Hopkins University Press. ISBN 0-8018-5413-X. OCLC 34515797.
- ^ Meyer, C. D. (2000). Matrix analysis and applied linear algebra. Philadelphia: Society for Industrial and Applied Mathematics. ISBN 0-89871-454-0. OCLC 43662189.
- ^ a b c d Trefethen, Lloyd N. (1997). Numerical linear algebra. David Bau. Philadelphia: Society for Industrial and Applied Mathematics. ISBN 0-89871-361-7. OCLC 36084666.



































































































![{\displaystyle \left[{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838a30dc9d065ec434dff490bd84061ed569db3b)
![{\displaystyle {\begin{aligned}|A-\lambda I|&=\left|{\begin{bmatrix}2&1\\1&2\end{bmatrix}}-\lambda {\begin{bmatrix}1&0\\0&1\end{bmatrix}}\right|={\begin{vmatrix}2-\lambda &1\\1&2-\lambda \end{vmatrix}}\\[6pt]&=3-4\lambda +\lambda ^{2}\\[6pt]&=(\lambda -3)(\lambda -1).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0084c80ab8c7637830cdf01f1c754f92a6598ac0)

































































