Konstanta Planck
| Nilai h | Satuan | Ref. |
|---|---|---|
| 6,626070150(81)×10−34 | J s | [1] |
| 4,135667662(25)×10−15 | eV s | [1] |
| 2π | EP tP | |
| Nilai ħ | Satuan | Ref. |
| 1,054571800(13)×10−34 | J s | [1] |
| 6,582119514(40)×10−16 | eV s | [1] |
| 1 | EP tP | def |
| Nilai hc | Satuan | Ref. |
| 1,98644568×10−25 | J m | |
| 1,23984193 | eV μm | |
| 2π | EP ℓP | |
| Nilai ħc | Satuan | Ref. |
| 3,16152649×10−26 | J m | |
| 0,19732697 | eV μm | |
| 1 | EP ℓP |

Konstanta Planck, dilambangkan dengan huruf h, adalah konstanta fisika untuk menjelaskan ukuran quanta. Konstanta ini sangat penting dalam teori mekanika kuantum, dan dinamai untuk menghargai Max Planck, salah seorang pendiri teori kuantum. Pertama kali diperkenalkan tahun 1900, konstanta ini pada awalnya merupakan konstanta kesebandingan antara kenaikan minimum energi, E dari sebuah osilator bermuatan listrik hipotesis pada rongga yang berisi radiasi benda-hitam, dan frekuensi, f dari gelombang elektromagnetiknya. Pada tahun 1905, nilai E, kenaikan energi minimum dari osilator hipotesis, dihubungkan secara teoretis oleh Albert Einstein dengan "kuantum" atau elemen energi terkecil dari gelombang elektromagnetik itu sendiri. Kuantum cahaya berperilaku seperti partikel listrik netral, sebagai lawan gelombang elektromagnetik. Nantinya disebut sebagai foton.
Hubungan Planck–Einstein menghubungkan energi foton E dengan frekuensi gelombang f:
Energi ini sangat kecil bila dilihat dari objek sehari-hari.
Mengingat bahwa frekuensi f, panjang gelombang λ, dan laju cahaya c saling berhubungan dengan , hubungan ini juga dapat dituliskan sebagai
Dengan p melambangkan momentum linear partikel (bukan hanya foton, tetapi juga fine particle lainnya), panjang gelombang de Broglie λ partikel dirumuskan dengan
Pada aplikasinya dimana digunakan frekuensi sudut (frekuensi dinyatakan dalam radian per detik bukan siklus per detik atau hertz) maka perlu dimasukkan faktor 2π ke dalam konstanta Planck. Hasil konstantanya disebut konstanta Planck tereduksi atau konstanta Dirac. Besarnya sama dengan konstanta Planck dibagi 2π, dan dilambangkan ħ (dibaca "h-bar"):
Energi foton dengan frekuensi sudut ω, dimana ω = 2πf, dirumuskan dengan
dan momentum linearnya sama dengan
dengan k adalah bilangan gelombang. Tahun 1923, Louis de Broglie menggeneralisasi hubungan Planck–Einstein dengan mempostulat bahwa konstanta Planck menyajikan kesebandingan antara momentum dan panjang gelombang bukan hanya foton, tetapi panjang gelombang kuantum partikel apapun. Hal ini dibuktikan dengan percobaan tidak lama kemudian.
Dua hubungan ini adalah bagian komponen spasial pernyataan relativitas khusus menggunakan 4-Vektor.
Mekanika statistik klasik membutuhkan adanya h (tapi tidak mendefinisikan nilainya).[2] Secara tidak sengaja, setelah penemuan Planck, diketahui bahwa aksi fisika tidak bisa menggunakan nilai bebas. Namun, harus merupakan perkalian jumlah yang sangat kecil, "kuantum aksi", saat ini disebut konstanta Planck.
Pada banyak kasus, seperti pada cahaya monokromatik atau untuk atom, kuantisasi energi juga berdampak bahwa hanya beberapa tingkat energi tertentu yang diperbolehkan, dan nilai diantaranya dilarang.[3]
Nilai[sunting | sunting sumber]
Nilainya kira-kira
- .
Konstanta Planck mempunyai satuan berupa energi dikalikan dengan waktu, yang tidak lain adalah satuan usaha. Satuan ini juga dapat ditulis sebagai momentum dikalikan dengan jarak (Nms), yaitu satuan momentum sudut.
Nilai yang berkaitan adalah Konstanta Planck yang dikurangi:
Simbol adalah bilangan pi. Konstanta ini, yang dibaca "h-bar", kadang-kadang disebut sebagai Konstanta Dirac, yang diambil dari nama Paul Dirac.
Awal mula[sunting | sunting sumber]
Radiasi benda-hitam[sunting | sunting sumber]
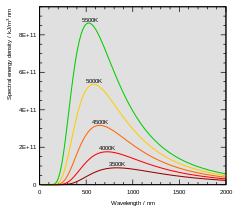
Pada tahun-tahun terakhir abad ke-19, Planck menginvestigasi masalah radiasi benda-hitam yang pertama kali dikemukakan oleh Kirchhoff sekitar 40 tahun sebelumnya. Diketahui bahwa objek panas akan bercahaya, makin panas maka cahayanya makin terang. Medan elektromagnetik mematuhi hukum gerak mirip seperti massa pada pegas, dan mencapai kesetimbangan termal dengan atom panas. Benda panas dalam kesetimbangan dengan cahaya menyerap sama banyak dengan yang dilepas. Jika bendanya hitam, maka ia menyerap semua cahaya yang masuk, maka emisi cahaya termalnya menjadi maksimum.
Asumsi bahwa radiasi benda-hitam adalah panas menuntun menuju sebuah prediksi akurat: total jumlah energi yang dilepas meningkat menurut temperatur menurut Hukum Stefan–Boltzmann (1879–84). Namun, diketahui juga bahwa warna cahaya yang ditunjukkan oleh benda panas berubah menurut temperatur, maka "panas putih" lebih panas daripada "panas merah". Wilhelm Wien menemukan hubungan matematis antara puncak berbagai kurva pada beberapa temperatur, menggunakan azas invarian adiabatik. Pada tiap temperatur, kurvanya bergeser menurut hukum perpindahan Wien (1893). Wien juga mengusulkan perkiraan untuk spektrum objek tersebut, yang nilainya tepat pada frekuensi tinggi (panjang gelombang pendek) namun tidak tepat pada frekuensi rendah (panjang gelombang tinggi).[4] Masih tidak jelas mengapa spektrum benda panas memiliki bentuk seperti itu (lihat diagram).
Planck melakukan hipotesis bahwa persamaan gerak untuk cahaya menjelaskan sekelompok osilator harmonis, satu untuk tiap frekuensi yang mungkin. Ia menguji bagaimana entropi osilator beragam menurut temperatur benda, mencoba untuk mencocokkan dengan hukum Wien, dan dapat menurunkan sebuah fungsi matematika untuk spektrum benda-hitam.[5]
Namun, Planck segera menyadari bahwa solusinya bukanlah satu-satunya. Ada beberapa solusi yang berbeda, tiap solusinya memberikan nilai entropi osilator yang berbeda.[5] Untuk menyelamatkan teorinya, Planck mennggunakan teori mekanika statistikanya yang kontroversial.[5][6] Salah satu kondisi batasnya adalah
untuk menafsirkan UN [energi getar osilator sejumlah N] tidak sebagai besaran yang kontinu, namun sebagai besaran diskret yang terdiri dari bagian bilangan bulat yang terbatas. Sebut saja tiap bagian ini elemen energi ε;
— Planck, On the Law of Distribution of Energy in the Normal Spectrum[5]
Dengan kondisi ini, Planck menentukan kuantisasi energi osilator,[7] yang nantinya akan merevolusionerkan fisika. Dengan pendekatan ini menunjukkan bahwa "elemen energi" berbanding lurus dengan frekuensi osilator, versi pertamanya saat ini diistilahkan dengan "hubungan Planck–Einstein":
Planck juga dapat menghitung nilai h dari data eksperimen radiasi benda-hitam: 6,55×10−34 J⋅s, hanya melenceng sekitar 1.2% dari nilai yang saat ini diterima.[5] Ia juga dapat menentukan nilai konstanta Boltzmann kB dari teori dan data yang sama.[8]
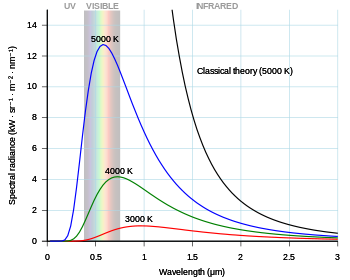
Sebelum Planck, telah diasumsikan bahwa energi benda dapat bernilai berapapun - itu merupakan variabel kontinu. Hukum Rayleigh–Jeans membuat prediksi yang mendekati untuk batasan temperatur tertentu, tapi hasilnya makin divergen ketika temperaturnya naik. Untuk menghasilkan Hukum Planck yang dapat memprediksi emisi benda hitam dengan baik, maka diperlukan untuk mengalikan pernyataan klasik dengan faktor kompleks yang mengikutsertakan h pada penyebut dan pembilangnya. Pengaruh h pada faktor kompleks ini tidak hilang jika diset menjadi nol atau nilai lainnya.
Permasalahan benda hitam muncul kembali tahun 1905, ketika Rayleigh dan Jeans (bersama) dan Einstein (di sisi lain) secara independen membuktikan bahwa elektromagnetisme klasik tidak dapat digunakan untuk spektrum yang teramati. Bukti ini dikenal dengan "bencana ultraungu", diistilahkan oleh Paul Ehrenfest tahun 1911. Mereka berkontribusi besar (bersama dengan kerja Einstein pada efek fotolistrik dalam meyakinkan fisikawan bahwa postulat Planck mengenai tingkat energi yang dikuantisasi lebih dari hanay sekadar formalisme matematika. Konferensi Solvay tahun 1911 didedikasikan untuk "teori radiasi dan kuanta".[9] Max Planck meraih Hadiah Nobel Fisika tahun 1918 untuk hasil kerjanya mendedikasikan untuk "kemajuan Fisika dengan penemuan kuanta energi".
Referensi[sunting | sunting sumber]
- ^ a b c d Barry N. Taylor of the Data Center in close collaboration with Peter J. Mohr of the Physical Measurement Laboratory's Atomic Physics Division, Termed the "2014 CODATA recommended values," they are generally recognized worldwide for use in all fields of science and technology. The values became available on 25 June 2015 and replaced the 2010 CODATA set. They are based on all of the data available through 31 December 2014. Available: http://physics.nist.gov
- ^ Giuseppe Morandi; F. Napoli; E. Ercolessi (2001), Statistical mechanics: an intermediate course, hlm. 84, ISBN 978-981-02-4477-4
- ^ Einstein, Albert (2003), "Physics and Reality" (PDF), Daedalus, 132 (4): 24, doi:10.1162/001152603771338742, diarsipkan dari versi asli (PDF) tanggal 2012-04-15, diakses tanggal 2017-01-13,
The question is first: How can one assign a discrete succession of energy value Hσ to a system specified in the sense of classical mechanics (the energy function is a given function of the coordinates qr and the corresponding momenta pr)? The Planck constant h relates the frequency Hσ/h to the energy values Hσ. It is therefore sufficient to give to the system a succession of discrete frequency values.
- ^ R. Bowley; M. Sánchez (1999), Introductory Statistical Mechanics (edisi ke-2nd), Oxford: Clarendon Press, ISBN 0-19-850576-0
- ^ a b c d e Planck, Max (1901), "Ueber das Gesetz der Energieverteilung im Normalspectrum" (PDF), Ann. Phys., 309 (3): 553–63, Bibcode:1901AnP...309..553P, doi:10.1002/andp.19013090310. English translation: "On the Law of Distribution of Energy in the Normal Spectrum Diarsipkan 2008-04-18 di Wayback Machine.".
- ^ Kragh, Helge (1 December 2000), Max Planck: the reluctant revolutionary, PhysicsWorld.com, diarsipkan dari versi asli tanggal 2012-04-01, diakses tanggal 2017-01-13
- ^ Kragh, Helge (1999), Quantum Generations: A History of Physics in the Twentieth Century, Princeton University Press, hlm. 62, ISBN 0-691-09552-3
- ^ Planck, Max (2 June 1920), The Genesis and Present State of Development of the Quantum Theory (Nobel Lecture)
- ^ Previous Solvay Conferences on Physics, International Solvay Institutes, diarsipkan dari versi asli tanggal 2008-12-16, diakses tanggal 12 December 2008













