Hukum sirkuit Kirchhoff
Hukum-hukum Sirkuit Kirchhoff adalah dua persamaan yang membahas kekekalan muatan dan energi dalam sirkuit listrik, dan pertama dijabarkan pada tahun 1845 oleh Gustav Kirchhoff. Hukum-hukum ini juga sering disebut sebagai Hukum Kirchhoff (lihat juga hukum Kirchhoff untuk arti lain) dan sering kali digunakan dalam teknik elektro
Kedua hukum sirkuit ini dapat diturunkan dari persamaan Maxwell, tetapi Kirchhoff ada sebelum Maxwell dan menggunakan pekerjaan dari Georg Ohm untuk menghasilkan hukumnya.
Hukum Arus Kirchhoff[sunting | sunting sumber]

Hukum ini juga disebut Hukum I Kirchhoff, Hukum titik Kirchhoff, Hukum percabangan Kirchhoff, atau KCL (Kirchhoff's Current Law).
Prinsip dari kekekalan muatan listrik mengatakan bahwa:
- Pada setiap titik percabangan dalam sirkuit listrik, jumlah dari arus yang masuk kedalam titik itu sama dengan jumlah arus yang keluar dari titik tersebut.
- atau
- Jumlah total arus pada sebuah titik adalah nol.
Mengingat bahwa arus adalah besaran bertanda (positif atau negatif) yang menunjukan arah arus tersebut menuju atau keluar dari titik, maka prinsip ini bisa dirumuskan menjadi:
n adalah jumlah cabang dengan arus yang masuk atau keluar terhadap titik tersebut.
Persamaan ini juga bisa digunakan untuk arus kompleks:
Hukum ini berdasar pada kekekalan muatan, dengan muatan (dalam satuan coulomb) adalah hasil kali dari arus (ampere) dan waktu (detik).
Padat muatan berubah[sunting | sunting sumber]
Hukum pertama Kirchhoff hanya dapat digunakan jika padat muatan konstan. Anggap arus masuk ke dalam sebuah lempeng dari kapasitor. Jika ada permukaan tertutup di sekitar satu (hanya satu dari dua) lempeng tersebut, arus masuk melalui permukaan tetapi tidak keluar, maka kasus ini melanggar hukum pertama Kirchhoff. Namun, arus yang melalui suatu permukaan yang melingkupi seluruh kapasitor (kedua lempeng) akan memenuhi hukum pertama Kirchhoff karena arus yang masuk ke dalam salah satu lempeng akan sama besar dengan arus yang keluar dari lempeng satunya, dan biasanya dalam analisis sirkuit hanya itu yang diperhitungkan, namun masalah akan muncul jika yang dilihat hanya satu lempeng. Contoh kasus lain dimana hukum ini tidak bekerja adalah arus pada antena. Karena pada antena, arus masuk ke dalam antena dari transmitter, tetapi tidak ada arus yang keluar dari ujung lainnya.
Maxwell memperkenalkan konsep arus perpindahan untuk menjelaskan kasus-kasus tersebut. Arus yang masuk ke dalam lempeng kapasitor sama dengan kecepatan akumulasi muatan maka juga sama dengan kecepatan perubahan fluks listrik karena muatan tersebut (fluks listrik juga menggunakan satuan coulomb seperti muatan listrik dalam satuan SI). Kecepatan perubahan fluks inilah, , yang disebut Maxwell sebagai arus perpindahan dan disatukan dengan rumus
Jika arus perpindahan digunakan, maka hukum pertama kirchhoff dapat berlaku kembali. Arus perpindahan bukanlah arus sebenarnya karena bukan berupa muatan yang bergerak, arus perpindahan hanyalah faktor koreksi untuk membuat hukum pertama Kirchhoff berlaku. Dalam kasus lempeng kapasitor, arus sebenarnya yang masuk ke dalam lempeng tersebut dihilangkan dengan jumlah yang sama oleh arus perpindahan yang meninggalkan lempeng tersebut dan menuju lempeng satunya.
Hal ini juga bisa dituliskan dengan menggunakan besaran medan vektor dengan menggunakan divergensi dari Hukum Ampère dan koreksi yang diberikan Maxwell, serta menggabungkan dengan hukum Gauss, menghasilkan:
Persamaan ini adalah persamaan kekekalan muatan (dalam bentuk integral, persamaan ini menyatakan bahwa jumlah arus yang keluar dari satu permukaan tertutup sama dengan kecepatan berkurangnya muatan dalam ruang yang ditutupi oleh permukaan tersebut (teorema divergensi).
Penggunaan[sunting | sunting sumber]
Hukum Kirchhoff dapat digunakan dengan matrix dan merupakan dasar dari hampir semua program simulasi sirkuit, seperti SPICE.
Hukum tegangan Kirchhoff[sunting | sunting sumber]
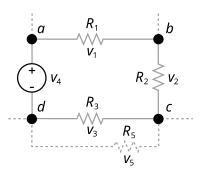
Hukum ini juga disebut sebagai Hukum kedua kirchhoff, Hukum putaran (loop) Kirchhoff, dan KVL (Kirchhoff's Voltage Law).
Prinsip kekekalan energi mengatakan bahwa
- Jumlah terarah (melihat orientasi tanda positif dan negatif) dari beda potensial listrik (tegangan) di sekitar sirkuit tertutup sama dengan nol.
- atau
- secara lebih sederhana, jumlah dari emf dalam lingkaran tertutup ekivalen dengan jumlah turunnya potensial pada lingkaran itu.
- atau
- Jumlah hasil kali resistansi konduktor dan arus pada konduktor dalam lingkaran tertutup sama dengan total emf yang ada dalam lingkaran (loop) itu.
Mirip dengan hukum pertama Kirchhoff, dapat ditulis sebagai:
Disini, n adalah jumlah tegangan listrik yang diukur. Tegangan listrik ini juga bisa berbentuk kompleks:
Hukum ini berdasarkan kekekalan "energi yang diserap atau dikeluarkan medan potensial" (tidak termasuk energi yang hilang karena disipasi). Diberikan sebuah tegangan listrik, suatu muatan tidak mendapat atau kehilangan energi setelah berputar dalam satu lingkaran sirkuit karena telah kembali ke potensial awal.
Hukum ini tetap berlaku walaupun resistansi (yang mengakibatkan disipasi energi) ada dalam sirkuit. Validitas hukum ini dalam kasus tadi dapat dimengerti dengan menyadari bahwa muatan tidak kembali ke tempat asalnya karena ada disipasi energi. Pada terminal negatif, muatan sudah hilang. Artinya energi yang diberikan oleh beda potensial sudah terpakai seluruhnya oleh resistansi yang mengubah energi tadi menjadi disipasi panas.
Medan listrik dan potensial listrik[sunting | sunting sumber]
Hukum kedua Kirchhoff dapat dianggap sebagai konsekuensi prinsip kekekalan energi.
Mengingat bahwa potensial listrik didefinisikan sebagai integral garis terhadap medan listrik, hukum kedua Kirchhoff dapat dituliskan sebagai
yang menyatakan bahwa integral garis medan listrik di sekitar lingkaran tertutup (loop) C adalah nol.
Untuk mengembalikannya ke bentuk khusus, integral ini dapat dipisah-pisah untuk mendapatkan tegangan pada komponen tertentu.mponents.
Keterbatasan[sunting | sunting sumber]
Hukum ini adalah penyederhanaan dari Hukum Induksi Faraday untuk kasus khusus dimana tidak ada fluktuasi medan magnet yang menyambungkan lingkaran tertutup (loop). Maka hukum ini cukup untuk menghitung sirkuit yang hanya berisi resistor dan kapasitor.
Lihat juga[sunting | sunting sumber]
Referensi[sunting | sunting sumber]
Artikel ini sudah memiliki daftar referensi, bacaan terkait, atau pranala luar, tetapi sumbernya belum jelas karena belum menyertakan kutipan pada kalimat. |
- Paul, Clayton R. (2001). Fundamentals of Electric Circuit Analysis. John Wiley & Sons. ISBN 0-471-37195-5.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 0-7167-0810-8.
- Howard W. Johnson, Martin Graham, High-speed signal propagation: advanced black magic, Prentice Hall Professional, 2003 ISBN 0-13-084408-X.
Pranala luar[sunting | sunting sumber]
- http://www.sasked.gov.sk.ca/docs/physics/u3c13phy.html[pranala nonaktif permanen]
- MIT video lecture on the KVL and KCL methods









