Wavelet
Teori wavelet adalah suatu konsep yang relatif baru yang dikembangkan. Kata “Wavelet” sendiri diberikan oleh Jean Morlet dan Alex Grossmann pada awal tahun 1980-an, dan kata ini berasal dari bahasa Prancis, “ondelette” yang berarti gelombang kecil. Kata “onde” yang berarti gelombang kemudian diterjemahkan ke bahasa Inggris menjadi “wave”, lalu digabung dengan kata aslinya sehingga terbentuk kata baru “wavelet”.
Transformasi Wavelet
[sunting | sunting sumber]Transformasi wavelet dibagi menjadi dua bagian besar, yaitu transformasi wavelet kontinu (TWK) dan transformasi wavelet diskrit (TWD).
Perbandingan dengan Transformasi Fourier
[sunting | sunting sumber]Sampai sekarang transformasi Fourier mungkin masih menjadi transformasi yang paling populer di area pemrosesan sinyal digital (PSD). Transformasi Fourier memberitahu kita informasi frekuensi dari sebuah sinyal, tapi tidak informasi waktu (kita tidak dapat tahu di mana frekuensi itu terjadi).
Karena itulah transformasi Fourier hanya cocok untuk sinyal stationari (sinyal yang informasi frekuensinya tidak berubah menurut waktu). Untuk menganalisis sinyal yang frekuensinya bervariasi di dalam waktu, diperlukan suatu transformasi yang dapat memberikan resolusi frekuensi dan waktu disaat yang bersamaan, biasa disebut analisis multi resolusi (AMR). AMR dirancang untuk memberikan resolusi waktu yang baik dan resolusi frekuensi yang buruk pada frekuensi tinggi suatu sinyal, serta resolusi frekuensi yang baik dan resolusi waktu yang buruk pada frekuensi rendah suatu sinyal. Pendekatan ini sangat berguna untuk menganalisis sinyal dalam aplikasi-aplikasi praktis yang memang memiliki lebih banyak frekuensi rendah.
Transformasi wavelet adalah suatu AMR yang dapat merepresentasikan informasi waktu dan frekuensi suatu sinyal dengan baik. Transformasi wavelet menggunakan sebuah jendela modulasi yang fleksibel, ini yang paling membedakannya dengan transformasi Fourier waktu-singkat (STFT), yang merupakan pengembangan dari transformasi Fourier. STFT menggunakan jendela modulasi yang besarnya tetap, ini menyebabkan dilema karena jendela yang sempit akan memberikan resolusi frekuensi yang buruk dan sebaliknya jendela yang lebar akan menyebabkan resolusi waktu yang buruk.
Transformasi Wavelet Kontinu
[sunting | sunting sumber]Cara kerja transformasi wavelet kontinu (TWK) adalah dengan menghitung konvolusi sebuah sinyal dengan sebuah jendela modulasi pada setiap waktu dengan setiap skala yang diinginkan. Jendela modulasi yang mempunyai skala fleksibel inilah yang biasa disebut induk wavelet atau fungsi dasar wavelet.
Dalam transformasi wavelet digunakan istilah translasi dan skala, karena istilah waktu dan frekuensi sudah digunakan oleh transformasi Fourier. Translasi adalah lokasi jendela modulasi saat digeser sepanjang sinyal, berhubungan dengan informasi waktu. Skala berhubungan dengan frekuensi, skala tinggi (frekuensi rendah) berhubungan dengan informasi global dari sebuah sinyal, sedangkan skala rendah (frekuensi tinggi) berhubungan dengan informasi detail.
TWK secara matematika dapat didefinisikan sebagai berikut:
Pada rumus di atas, menyatakan fungsi sinyal setelah transformasi, dengan variabel s (skala) dan (translasi) sebagai dimensi baru. Fungsi menyatakan sinyal asli sebelum transformasi. Fungsi dasar disebut sebagai wavelet, dengan * menunjukkan konjugasi kompleks.
Dan inversi dari TWK secara matematika dapat didefinisikan sebagai berikut:
Seperti telah dibicarakan sebelumnya, fungsi dasar wavelet dapat didesain sesuai kebutuhan untuk mendapatkan hasil transformasi yang terbaik, ini perbedaan mendasar dengan transformasi Fourier yang hanya menggunakan fungsi sinus sebagai jendela modulasi.

Fungsi dasar wavelet secara matematika dapat didefinisikan sebagai berikut:
faktor digunakan untuk normalisasi energi pada skala yang berubah-ubah.
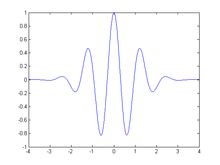
Mexican Hat, yang merupakan normalisasi dari derivatif kedua fungsi Gaussian adalah salah satu contoh fungsi dasar TWK:
Contoh lain adalah fungsi dasar Morlet, yang merupakan fungsi bilangan kompleks:
dengan dan
Transformasi Wavelet Diskrit
[sunting | sunting sumber]Dibandingkan dengan TWK, transformasi wavelet diskrit (TWD) dianggap relatif lebih mudah pengimplementasiannya. Prinsip dasar dari TWD adalah bagaimana cara mendapatkan representasi waktu dan skala dari sebuah sinyal menggunakan teknik pemfilteran digital dan operasi sub-sampling.
Sinyal pertama-tama dilewatkan pada rangkaian filter high-pass dan low-pass, kemudian setengah dari masing-masing keluaran diambil sebagai sampel melalui operasi sub-sampling. Proses ini disebut sebagai proses dekomposisi satu tingkat. Keluaran dari filter low-pass digunakan sebagai masukkan di proses dekomposisi tingkat berikutnya. Proses ini diulang sampai tingkat proses dekomposisi yang diinginkan. Gabungan dari keluaran-keluaran filter high-pass dan satu keluaran filter low-pass yang terakhir, disebut sebagai koefisien wavelet, yang berisi informasi sinyal hasil transformasi yang telah terkompresi.
Berkat operasi sub-sampling yang menghilangkan informasi sinyal yang berlebihan, transformasi wavelet telah menjadi salah satu metode kompresi data yang paling handal. Biro investigasi federal (FBI) Amerika Serikat menggunakan metode ini dalam proses kompresi data sidik jari mereka.
Pasangan filter high-pass dan low-pass yang digunakan harus merupakan quadrature mirror filter (QMF), yaitu pasangan filter yang memenuhi persamaan berikut:
dengan h[n] adalah filtar high-pass, g[n] adalah filter low-pass dan L adalah panjang masing-masing filter.
Aplikasi
[sunting | sunting sumber]artikel ini perlu dirapikan agar memenuhi standar Wikipedia. |
TWK umumnya digunakan di dalam penelitian ilmiah sedangkan TWD lebih banyak dipakai dalam aplikasi teknik dan komputer.
Beberapa contoh aplikasi:
TWK
[sunting | sunting sumber]- Fisika
- Kimia
- Biologi
- Teknik
- Respon transien
- Respon impuls
- Analisis nilai jenuh
- Pengenalan suara
TWD
[sunting | sunting sumber]- Proses de-noising sinyal
- Kompresi data
- Pengolahan gambar
- Penghitungan matriks nilai eigen
Lihat pula
[sunting | sunting sumber]Referensi
[sunting | sunting sumber]- Wavelet Tutorial Diarsipkan 2018-04-30 di Wayback Machine.
- A Very Friendly Guide to Wavelet
- Wavelet and Signal Processing
Pranala luar
[sunting | sunting sumber]- Komunitas Wavelet Diarsipkan 2020-09-29 di Wayback Machine.














![{\displaystyle h[L-1-n]=(-1)^{n}\cdot g[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b14a23ebbad72dbe36f85f79465e24c932463f23)