Metode Heun
Dalam matematika dan komputasi, metode Heun dapat merujuk pada peningkatan[1] atau metode Euler yang dimodifikasi (yaitu, aturan trapesium eksplisit[2]), atau metode Runge-Kutta dua tahap yang serupa. Namanya Karl Heun dan merupakan prosedur numerik untuk menyelesaikan persamaan diferensial biasa dengan nilai awal yang diberikan. Kedua varian dapat dilihat sebagai ekstensi metode Euler menjadi metode Runge-Kutta orde dua tahap kedua.
Prosedur untuk menghitung solusi numerik untuk masalah nilai awal:
dengan cara metode Heun, adalah pertama menghitung nilai antara dan kemudian perkiraan akhir pada titik integrasi berikutnya.
di mana adalah ukuran langkah dan .
Deskripsi
[sunting | sunting sumber]Metode Euler digunakan sebagai dasar untuk metode Heun. Metode Euler menggunakan garis tangen ke fungsi di awal interval sebagai perkiraan kemiringan fungsi selama interval, dengan asumsi bahwa jika ukuran langkah kecil, kesalahan akan menjadi kecil. Namun, bahkan ketika ukuran langkah sangat kecil digunakan, lebih dari sejumlah besar langkah kesalahan mulai menumpuk dan estimasi menyimpang dari nilai fungsional aktual.
Di mana kurva solusi cekung ke atas, garis singgungnya akan meremehkan koordinat vertikal dari titik berikutnya dan sebaliknya untuk solusi cekung ke bawah. Garis prediksi ideal akan mengenai kurva pada titik prediksi berikutnya. Pada kenyataannya, tidak ada cara untuk mengetahui apakah solusinya cekung atau cekung, dan karenanya jika titik prediksi selanjutnya akan melebih-lebihkan atau meremehkan nilai vertikalnya. Konkavitas kurva tidak dapat dijamin untuk tetap konsisten dan prediksi dapat melebih-lebihkan dan meremehkan pada titik yang berbeda dalam domain solusi. Metode Heun mengatasi masalah ini dengan mempertimbangkan interval yang direntang oleh segmen garis singgung secara keseluruhan. Mengambil contoh cekung, garis prediksi tangen kiri meremehkan kemiringan kurva untuk seluruh lebar interval dari titik saat ini ke titik prediksi berikutnya. Jika garis singgung pada titik ujung kanan dianggap (yang dapat diperkirakan dengan menggunakan Metode Euler), ia memiliki masalah yang berlawanan[3] Titik-titik di sepanjang garis singgung dari titik ujung kiri memiliki koordinat vertikal yang semuanya meremehkan orang-orang yang bersandar pada kurva solusi, termasuk titik ujung kanan interval yang dipertimbangkan. Solusinya adalah membuat kemiringan lebih besar dengan jumlah tertentu. Metode Heun mempertimbangkan garis singgung ke kurva solusi di kedua ujung interval, yang terlalu tinggi , dan yang meremehkan koordinat vertikal yang ideal. Garis prediksi harus dibangun berdasarkan kemiringan tangen titik ujung kanan saja, diperkirakan menggunakan Metode Euler. Jika kemiringan ini melewati titik ujung kiri dari interval, hasilnya jelas terlalu curam untuk digunakan sebagai garis prediksi ideal dan melebih-lebihkan titik ideal. Oleh karena itu, titik ideal terletak kira-kira di tengah-tengah antara perkiraan yang salah dan terlalu rendah, rata-rata dari dua lereng.
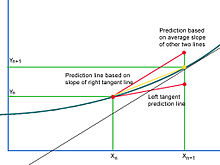
Metode Euler digunakan untuk memperkirakan secara kasar koordinat titik berikutnya dalam solusi, dan dengan pengetahuan ini, perkiraan awal diprediksi ulang atau diperbaiki.[4] Dengan asumsi kuantitas di sisi kanan persamaan dapat dianggap sebagai kemiringan dari solusi yang dicari di titik mana pun , ini dapat dikombinasikan dengan estimasi Euler dari titik berikutnya untuk memberikan kemiringan garis singgung di titik akhir kanan. Selanjutnya rata-rata kedua lereng digunakan untuk menemukan koordinat yang diperbaiki dari interval ujung kanan.
Derivasi
[sunting | sunting sumber]Dengan menggunakan prinsip bahwa kemiringan garis sama dengan naik / turunnya, koordinat pada akhir interval dapat ditemukan menggunakan rumus berikut:
- ,
Keakuratan metode Euler hanya meningkat secara linier dengan ukuran langkah berkurang, sedangkan Metode Heun meningkatkan akurasi secara kuadratik.[5] Skema ini dapat dibandingkan dengan metode trapesium implisit, tetapi dengan digantikan oleh untuk membuatnya eksplisit. adalah hasil dari satu langkah metode Euler pada masalah nilai awal yang sama. Jadi, metode Heun adalah metode prediktor-korektor dengan metode maju Euler sebagai prediktor dan metode trapesium sebagai korektor.
Metode Runge-Kutta
[sunting | sunting sumber]Metode Euler yang ditingkatkan adalah metode Runge-Kutta dua tahap, dan dapat ditulis menggunakan tablo Butcher (setelah John C. Butcher):
| 0 | |||
| 1 | 1 | ||
| 1/2 | 1/2 |
Metode lain yang disebut sebagai metode Heun (juga dikenal sebagai metode Ralston) memiliki tabel Jagal:[6]
| 0 | |||
| 2/3 | 2/3 | ||
| 1/4 | 3/4 |
Metode ini meminimalkan kesalahan pemotongan.
Referensi
[sunting | sunting sumber]- ^ Süli, Endre; Mayers, David (2003), An Introduction to Numerical Analysis, Cambridge University Press, ISBN 0-521-00794-1.
- ^ Ascher, Uri M.; Petzold, Linda R. (1998), Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-412-8.
- ^ "Numerical Methods for Solving Differential Equations". San Joaquin Delta College. Diarsipkan dari versi asli tanggal 2009-02-12.
- ^ Chen, Wenfang.; Kee, Daniel D. (2003), Advanced Mathematics for Engineering and Science, MA, USA: World Scientific, ISBN 981-238-292-5.
- ^ "The Euler-Heun Method" (PDF). LiveToad.org. Diarsipkan dari versi asli (PDF) tanggal 2016-03-04. Diakses tanggal 2019-12-16.
- ^ Leader, Jeffery J. (2004), Numerical Analysis and Scientific Computation, Boston: Addison-Wesley, ISBN 0-201-73499-0.





![{\displaystyle y_{i+1}=y_{i}+{\frac {h}{2}}[f(t_{i},y_{i})+f(t_{i+1},{\tilde {y}}_{i+1})],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4de50045f6b3fe877e7109e855e63a72c78663e2)















