Aksioma

Aksioma Matematika yang disebut dengan postulat

Aksioma, postulat atau asumsi adalah pernyataan yang berfungsi sebagai premis atau titik awal untuk alasan dan argumen lebih lanjut. Aksioma diartikan juga sebagai suatu pernyataan yang memuat istilah dasar dan istilah terdefinisi dan tidak berdiri sendiri dan tidak diuji kebenarannya. Akan tetapi, aksioma dalam matematika bukan berarti proposisi yang terbukti dengan sendirinya. Melainkan, suatu titik awal dari sistem logika. Misalnya, $1+1=2$ Nama lain dari aksioma adalah postulat. Suatu aksioma adalah basis dari sistem logika formal yang bersama-sama dengan aturan inferensi mendefinisikan logika. Pada akhirnya aksioma merupakan sebuah pernyataan yang sudah pasti kebenarannya.

Istilah aksioma paling umum digunakan sebagai istilah dalam matematika, sasaran atau objek penelahan matematika yang berupa fakta, konsep, operasi dan prinsip memerlukan metode tertentu dalam menemukan kebenaran atau keabsahan dari konsep yang terkandung didalamnya. Objek penelaahan tersebut menggunakan simbol-simbol yang kosong dari arti, artinya bahwa setiap simbol yang digunakan dalam matematika merupakan simbol abstrak. Ciri ini yang memungkinkan matematika dapat memasuki wilayah bidang studi atau cabang ilmu lain. Pada hakekatnya berpikir matematika itu dilandasi oleh kesepakatan-kesepakatan yang disebut aksioma. Karena itu matematika merupakan sistem yang aksiomatik.

Salah satu fenomena tentang aksioma yang ada adalah Selama 2000 tahun aksioma tentang bilangan dan geometri dianggap sebagai suatu kebenaran yang pasti karena teorema merupakan konsekuensi logis dari aksioma, maka teorema pun dianggap sebagai kebenaran yang tidak terbantahkan lagi.

Defenisi

Kata aksioma berasal dari bahasa Yunani kata ἀξίωμα (Axioma), sebuah verbal noun dari ἀξιόειν kata kerja (Axioein), yang berarti "untuk menganggap layak", tetapi juga "membutuhkan", yang pada gilirannya berasal dari ἄξιος ( áxios ), yang berarti "seimbang", dan karenanya "memiliki (sama) nilai (sebagai)", "layak", "pantas". Di antara para filosof Yunani kuno, sebuah aksioma adalah klaim yang dapat dilihat sebagai kebenaran yang terbukti dengan sendirinya tanpa perlu pembuktian.

Istilah aksioma juga dimengerti dalam matematika.Kata aksioma dalam matematika juga disebut postulat. Arti dasar dari kata postulat adalah "menuntut"; misalnya, Euclid menuntut agar seseorang setuju bahwa beberapa hal dapat dilakukan (misalnya, dua titik mana pun dapat digabungkan dengan garis lurus).

Geometri kuno mempertahankan beberapa perbedaan antara aksioma dan postulat. Saat mengomentari buku-buku Euclid, Proclus menyatakan bahwa " Geminus berpendapat bahwa Postulat [4] ini tidak boleh digolongkan sebagai postulat tetapi sebagai aksioma, karena tidak, seperti tiga Postulat pertama, menegaskan kemungkinan beberapa konstruksi tetapi mengungkapkan suatu properti penting." Boethius menerjemahkan 'postulat' sebagai petitio dan menyebut aksioma notiones communes tetapi dalam manuskrip-manuskrip selanjutnya penggunaan ini tidak selalu dijaga dengan ketat.

Sejarah

Yunani awal

Metode logika-deduktif dimana kesimpulan (pengetahuan baru) mengikuti dari premis (pengetahuan lama) melalui penerapan argumen suara ( silogisme, aturan inferensi ) dikembangkan oleh orang Yunani kuno, dan telah menjadi prinsip inti matematika modern. Tautologi dikecualikan, tidak ada yang dapat disimpulkan jika tidak ada yang diasumsikan. Aksioma dan postulat dengan demikian asumsi dasar yang mendasari tubuh tertentu pengetahuan deduktif. Mereka diterima tanpa demonstrasi. Semua pernyataan lain ( teorema, dalam kasus matematika) harus dibuktikan dengan bantuan asumsi dasar ini. Namun, interpretasi pengetahuan matematika telah berubah dari zaman kuno ke modern, dan akibatnya istilah aksioma dan postulat memiliki arti yang sedikit berbeda untuk matematikawan masa kini, daripada yang mereka lakukan untuk Aristoteles dan Euclid.

Orang Yunani kuno menganggap geometri hanya sebagai salah satu dari beberapa ilmu pengetahuan, dan menganggap teorema geometri setara dengan fakta ilmiah. Dengan demikian, mereka mengembangkan dan menggunakan metode logika-deduktif sebagai sarana untuk menghindari kesalahan, dan untuk menyusun dan mengkomunikasikan pengetahuan. Analisis posterior Aristoteles adalah eksposisi definitif dari pandangan klasik. Sebuah "aksioma", dalam terminologi klasik, mengacu pada asumsi yang terbukti dengan sendirinya umum untuk banyak cabang ilmu pengetahuan. Contoh yang baik adalah pernyataan bahwa "Ketika jumlah yang sama diambil dari yang sama, hasil jumlah yang sama."

Di dasar berbagai ilmu terdapat hipotesis tambahan tertentu yang diterima tanpa bukti. Hipotesis semacam itu disebut postulat . Sementara aksioma yang umum untuk banyak ilmu pengetahuan, postulat masing-masing ilmu tertentu berbeda. Validitas mereka harus ditetapkan melalui pengalaman dunia nyata. Aristoteles memperingatkan bahwa isi suatu ilmu tidak dapat berhasil dikomunikasikan jika pelajar ragu-ragu tentang kebenaran postulat.

Pendekatan klasik diilustrasikan dengan baik oleh Euclid's Elements, di mana daftar postulat diberikan (fakta geometris yang masuk akal diambil dari pengalaman kami), diikuti oleh daftar "gagasan umum" (sangat mendasar, self -pernyataan yang jelas).

Postulat

1. Dimungkinkan untuk menggambar garis lurus dari titik mana pun ke titik lainnya.
2. Dimungkinkan untuk memperpanjang segmen garis secara terus menerus di kedua arah.
3. Dimungkinkan untuk menggambarkan lingkaran dengan pusat dan jari-jari apa pun.
4. Memang benar bahwa semua sudut siku -siku sama besar satu sama lain.
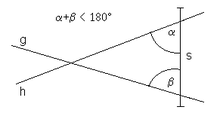
5. (" Postulat Sejajar ") Memang benar bahwa, jika garis lurus yang jatuh pada dua garis lurus membuat sudut-sudut dalam pada sisi yang sama kurang dari dua sudut siku-siku, dua garis lurus, jika dibuat tanpa batas, berpotongan pada sisi yang sudut yang lebih kecil dari dua sudut siku-siku.

Gagasan umum

1. Hal-hal yang sama dengan hal yang sama juga sama satu sama lain.
2. Jika sama ditambahkan ke sama, keutuhannya sama.
3. Jika yang sama dikurangkan dari yang sama, maka sisanya adalah sama.
4. Hal-hal yang bertepatan satu sama lain adalah sama satu sama lain.
5. Keseluruhan lebih besar daripada bagian.

Zaman modern

Pelajaran yang dipetik oleh matematika dalam 150 tahun terakhir adalah berguna untuk melepaskan makna dari pernyataan matematika (aksioma, postulat, proposisi, teorema) dan definisi. Seseorang harus mengakui perlunya gagasan primitif, atau istilah atau konsep yang tidak ditentukan, dalam studi apa pun. Abstraksi atau formalisasi semacam itu membuat pengetahuan matematika lebih umum, mampu memiliki banyak arti yang berbeda, dan oleh karena itu berguna dalam berbagai konteks. Alessandro Padoa, Mario Pieri, dan Giuseppe Peano adalah pionir dalam gerakan ini.

Matematika strukturalis melangkah lebih jauh, dan mengembangkan teori-teori dan aksioma (misalnya teori medan, teori grup, topologi, ruang vektor ) tanpa aplikasi tertentu dalam pikiran. Perbedaan antara "aksioma" dan "postulat" menghilang. Postulat-postulat Euclid dimotivasi secara menguntungkan dengan mengatakan bahwa postulat-postulat itu mengarah pada kekayaan besar fakta-fakta geometris. Kebenaran dari fakta-fakta rumit ini bertumpu pada penerimaan hipotesis dasar. Namun, dengan membuang postulat kelima Euclid, seseorang bisa mendapatkan teori yang memiliki makna dalam konteks yang lebih luas (misalnya, geometri hiperbolik ). Dengan demikian, seseorang harus siap untuk menggunakan label seperti "garis" dan "paralel" dengan fleksibilitas yang lebih besar. Perkembangan geometri hiperbolik mengajarkan matematikawan bahwa berguna untuk menganggap postulat sebagai pernyataan formal murni, dan bukan sebagai fakta berdasarkan pengalaman.

Ketika matematikawan menggunakan aksioma lapangan, niatnya bahkan lebih abstrak. Proposisi teori medan tidak menyangkut satu aplikasi tertentu; matematikawan sekarang bekerja dalam abstraksi lengkap. Ada banyak contoh bidang; teori medan memberikan pengetahuan yang benar tentang mereka semua.

Tidak benar untuk mengatakan bahwa aksioma teori medan adalah "proposisi yang dianggap benar tanpa bukti". Sebaliknya, aksioma lapangan adalah satu set kendala. Jika ada sistem penjumlahan dan perkalian yang memenuhi batasan ini, maka seseorang berada dalam posisi untuk segera mengetahui banyak informasi tambahan tentang sistem ini.

Matematika modern memformalkan fondasinya sedemikian rupa sehingga teori matematika dapat dianggap sebagai objek matematika, dan matematika itu sendiri dapat dianggap sebagai cabang logika . Frege, Russell, Poincaré, Hilbert, dan Gödel adalah beberapa tokoh kunci dalam perkembangan ini.

Pelajaran lain yang dipelajari dalam matematika modern adalah memeriksa bukti-bukti yang diakui secara hati-hati untuk asumsi-asumsi yang tersembunyi.

Dalam pemahaman modern, seperangkat aksioma adalah kumpulan pernyataan yang dinyatakan secara formal yang diikuti oleh pernyataan lain yang dinyatakan secara formal – dengan penerapan aturan tertentu yang terdefinisi dengan baik. Dalam pandangan ini, logika hanya menjadi sistem formal lainnya. Serangkaian aksioma harus konsisten ; seharusnya tidak mungkin untuk menurunkan kontradiksi dari aksioma. Serangkaian aksioma juga harus tidak berlebihan; pernyataan yang dapat disimpulkan dari aksioma lain tidak perlu dianggap sebagai aksioma.

Itu adalah harapan awal ahli logika modern bahwa berbagai cabang matematika, mungkin semua matematika, dapat diturunkan dari kumpulan aksioma dasar yang konsisten. Keberhasilan awal dari program formalis adalah formalisasi Hilbert dari geometri Euclidean, dan demonstrasi terkait dari konsistensi aksioma tersebut.

Dalam konteks yang lebih luas, ada upaya untuk mendasarkan semua matematika pada teori himpunan Cantor . Di sini, munculnya paradoks Russell dan antinomi serupa dari teori himpunan naif meningkatkan kemungkinan bahwa sistem semacam itu bisa berubah menjadi tidak konsisten.

Proyek formalis mengalami kemunduran yang menentukan, ketika pada tahun 1931 Gödel menunjukkan bahwa adalah mungkin, untuk setiap set aksioma yang cukup besar ( aksioma Peano, misalnya) untuk membangun sebuah pernyataan yang kebenarannya tidak tergantung pada set aksioma tersebut. Sebagai akibat wajar, Gödel membuktikan bahwa konsistensi teori seperti aritmatika Peano adalah pernyataan yang tidak dapat dibuktikan dalam ruang lingkup teori itu.

Masuk akal untuk percaya pada konsistensi aritmatika Peano karena dipenuhi oleh sistem bilangan asli, sistem formal yang tak terbatas tetapi dapat diakses secara intuitif. Namun, saat ini, tidak ada cara yang diketahui untuk menunjukkan konsistensi aksioma Zermelo–Fraenkel modern untuk teori himpunan. Selanjutnya, dengan menggunakan teknik pemaksaan ( Cohen ) seseorang dapat menunjukkan bahwa hipotesis kontinum (Cantor) tidak bergantung pada aksioma Zermelo–Fraenkel. Jadi, bahkan rangkaian aksioma yang sangat umum ini tidak dapat dianggap sebagai landasan definitif untuk matematika.

Logika matematika

Di bidang logika matematika, perbedaan yang jelas dibuat antara dua pengertian aksioma: logis dan non-logis (agak mirip dengan perbedaan kuno antara "aksioma" dan "postulat" masing-masing).

Sistem aksioma

Ini adalah rumus -rumus tertentu dalam bahasa formal yang berlaku universal, yaitu rumus-rumus yang dipenuhi oleh setiap penetapan nilai. Biasanya seseorang mengambil sebagai aksioma logis setidaknya beberapa tautologi minimal yang cukup untuk membuktikan semua tautologi dalam bahasa; dalam kasus logika predikat aksioma lebih logis dari yang diperlukan, untuk membuktikan kebenaran logis yang tidak tautologi dalam arti yang ketat.

Contoh

Dalam logika proposisional adalah umum untuk mengambil sebagai aksioma logis semua rumus dari bentuk berikut, di mana: $\phi$, $\chi$, dan $\psi$ dapat berupa formula bahasa apa pun dan di mana penghubung primitif yang disertakan hanya " $\neg$ " untuk negasi dari proposisi segera berikut dan " $\to$ " untuk implikasi dari proposisi anteseden ke konsekuen

1. $\phi \to (\psi \to \phi )$
2. $(\phi \to (\psi \to \chi ))\to ((\phi \to \psi )\to (\phi \to \chi ))$
3. $(\lnot \phi \to \lnot \psi )\to (\psi \to \phi ).$

Masing-masing pola ini adalah skema aksioma, aturan untuk menghasilkan aksioma dalam jumlah tak terbatas. Misalnya, jika $A$, $B$, dan $C$ adalah variabel proposisi, maka $A\to (B\to A)$ dan $(A\to \lnot B)\to (C\to (A\to \lnot B))$ keduanya merupakan contoh dari skema aksioma 1, dan karenanya merupakan aksioma. Dapat ditunjukkan bahwa hanya dengan tiga skema aksioma dan modus ponens, seseorang dapat membuktikan semua tautologi kalkulus proposisional. Juga dapat ditunjukkan bahwa tidak ada pasangan skema ini yang cukup untuk membuktikan semua tautologi dengan modus ponens.

Lihat pula

• Sistem aksiomatik
• Dogma
• Prinsip pertama, aksioma dalam sains dan filsafat
• Daftar aksioma
• Teori model
• Regulæ Juris
• Teorema
• Presuposisi
• Hukum fisika
• Prinsip

Bacaan lebih lanjut

• Mendelson, Elliot (1987). Introduction to mathematical logic. Belmont, California: Wadsworth & Brooks. ISBN 0-534-06624-0
• Wilson, John Cook (1889). On an Evolutionist Theory of Axioms. Oxford: Clarendon Press. 

Pranala luar

• (Inggris) Aksioma at PhilPapers
• Artikel ini berisikan material dari Axiom, yang berada di bawah lisensi Creative Commons Atribusi/Berbagi-Bersama.
• Metamath axioms page