Teori VSEPR
Teori VSEPR (Valence Shell Electron Pair Repulsion: "tolakan pasangan kulit elektron valensi") adalah suatu model kimia yang digunakan untuk menjelaskan bentuk-bentuk molekul kimiawi berdasarkan gaya tolakan elektrostatik antar pasangan elektron.[1] Teori ini juga dinamakan teori Gillespie-Nyholm, dinamai atas dua orang pengembang teori ini. Akronim "VSEPR" diucapkan sebagai "vesper" untuk kemudahan pengucapan.
Premis utama teori VSEPR adalah bahwa pasangan elektron valensi disekitar atom akan saling tolak menolak, sehingga susunan pasangan elektron tersebut akan mengadopsi susunan yang meminimalisasi gaya tolak menolak. Minimalisasi gaya tolakan antar pasangan elektron ini akan menentukan geometri molekul. Jumlah pasangan elektron di sekitar atom disebut sebagai bilangan sterik.
Teori VSEPR biasanya akan dibandingkan dengan teori ikatan valensi yang mengalamatkan bentuk molekul melalui orbital yang secara energetika dapat melakukan ikatan. Teori ikatan valensi berkutat pada pembentukan ikatan sigma dan pi. Teori orbital molekul adalah model lainnya yang digunakan untuk menjelaskan bagaimana atom dan elektron tersusun menjadi molekul dan ion poliatomik.
Teori VSEPR telah lama dikritik oleh karena teori ini tidak memiliki perumusan yang kuantitatif, sehingga teori ini hanya dapat digunakan untuk memprediksi bentuk molekul secara "kasar", walaupun cukup akurat.
Sejarah[sunting | sunting sumber]
Gagasan bahwa terdapat suatu korelasi antara geometri molekul dengan jumlah elektron valensi pertama kali dicetuskan oleh Sidgwick dan Powell pada tahun 1940.[2] Pada tahun 1957, Gillespie dan Nyholm menyempurnakan konsep ini untuk membangun suatu teori yang mampu memprediksi geometri molekul.[3][4]
Penjelasan[sunting | sunting sumber]
Teori VSEPR utamanya melibatkan prediksi susunan pasangan elektron di sekitar satu atau lebih atom pusat pada suatu molekul. Jumlah pasangan elektron pada kelopak valensi atom pusat ditentukan dengan menggambarkan struktur Lewis molekul tersebut. Ketika terdapat dua atau lebih struktur resonansi yang dapat mewakili suatu molekul, model VSEPR dapat diterapkan pada semua struktur resonansi tersebut. Pada teori VSEPR, pasangan elektron berganda pada ikatan berganda diperlakukan sebagai "satu pasang" elektron.
Pasangan elektron diasumsikan berada pada permukaan bola yang berpusat pada atom pusat. Oleh karena pasangan elektron tersebut bermuatan negatif, kesemuaan pasangan elektron akan menduduki posisi yang meminimalisasi gaya tolak menolak antar sesamanya dengan memaksimalkan jarak antar pasangan elektron. Jumlah pasangan elektron oleh karenanya akan menentukan keseluruhan geometri molekul.
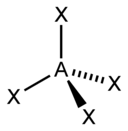
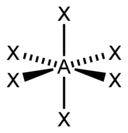
Sebagai contoh, ketika terdapat dua pasang elektron di sekitar atom pusat, gaya tolak-menolak di antara keduanya akan menjadi minimal ketika keduanya berada pada posisi saling berseberangan. Oleh karena itu, atom pusat diprediksikan mengadopsi geometri linear. Jika terdapat tiga pasang elektron, maka gaya tolak-menolak diminimalkan dengan mengadopsi bentuk trigonal. Dengan cara yang sama, untuk empat pasang elektron, susunan geometri yang optimal adalah tetrahedral.
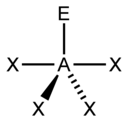
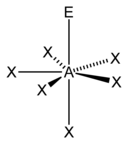
Prediksi keseluruhan geometri ini disempurnakan lebih jauh dengan membedakan pasangan elektron ikatan dan non-ikatan. Pasangan elektron ikatan terlibat dalam ikatan sigma dengan atom bersebelahan, sehingga kedua elektron tersebut dikongsi oleh dua atom yang berikatan, menyebabkan pasangan elektron tersebut berada lebih jauh dari atom pusat daripada pasangan elektron non-ikatan (pasangan elektron menyendiri) yang akan berada lebih dekat dengan atom pusat. Oleh karena itu, tolakan yang diakibatkan oleh pasangan elektron menyendiri akan lebih besar daripada tolakan yang diakibatkan oleh pasangan elektron yang berikatan. Dengan demikian, ketika geometri molekul memiliki dua set posisi yang menerima gaya tolak-menolak dengan derajat yang berbeda, pasangan elektron menyendiri akan cenderung menduduki posisi yang menerima gaya tolakan lebih kecil. Dengan kata lain, gaya tolak menolak antara pasangan elektron menyendiri dengan pasangan elektron menyendiri (lone pair - lone pair) akan lebih kuat daripada gaya tolak menolak antara pasangan elektron menyendiri dengan pasangan elektron berikatan (lone pair - bonding pair), yang juga sendiri lebih kuat daripada gaya tolak-menolak antara pasangan elektron berikatan dengan pasangan elektron berikatan (bonding pair - bonding pair). Secara ringkas dapat ditulis: lp-lp > lp-bp > bp-bp.
Pembedaan ini sangat penting utamanya ketika dalam suatu geometri molekul terdapat dua atau lebih posisi yang memungkinkan.
Metode AXE[sunting | sunting sumber]
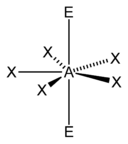
Metode perhitungan elektron AXE umumnya digunakan ketika kita menerapkan teori VSEPR. A mewakili atom pusat. X mewakili jumlah ikatan sigma antara atom pusat dengan atom luar. Ikatan ganda kovalen dihitung sebagai satu X. E mewakili jumlah pasangan elektron menyendiri yang ada disekitar atom pusat. Jumlah X dan E, disebut sebagai bilangan sterik juga diasosiasikan dengan jumlah orbital hibridisasi yang digunakan dalam teori ikatan valensi.
Berdasarkan jumlah bilangan sterik dan distribusi X serta E, teori VSEPR akan memberikan prediksi sebagai berikut:
| Jenis molekul | Bentuk | Susunan elektron | Geometri | Contoh |
|---|---|---|---|---|
| AX1En | Diatomik | HF, O2 | ||
| AX2E0 | Linear | BeCl2, HgCl2, CO2 | ||
| AX2E1 | Tekuk | 
|

|
NO2−, SO2, O3 |
| AX2E2 | Tekuk | 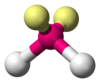
|

|
H2O, OF2 |
| AX2E3 | Linear | 
|
XeF2, I3− | |
| AX3E0 | Datar trigonal | 
|

|
BF3, CO32−, NO3−, SO3 |
| AX3E1 | Piramida trigonal | 
|

|
NH3, PCl3 |
| AX3E2 | Bentuk T | 
|

|
ClF3, BrF3 |
| AX4E0 | Tetrahedral | 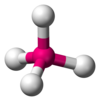
|

|
CH4, PO43−, SO42−, ClO4− |
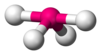
| AX4E1 | Jungkat-jungkit | 
|
|
SF4 |
| AX4E2 | Datar persegi | 
|

|
XeF4 |
| AX5E0 | Bipiramida trigonal | 
|

|
PCl5 |
| AX5E1 | Piramida persegi | 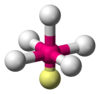
|

|
ClF5, BrF5 |
| AX5E2 | Datar pentagonal | 
|

|
XeF5− |
| AX6E0 | Oktahedral | 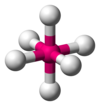
|

|
SF6 |
| AX6E1 | Piramida pentagonal | 
|

|
XeOF5−, IOF52−[5] |
| AX7E0 | Bipiramida pentagonal | 
|

|
IF7 |
Ketika atom substituen (X) tidak sama, geometri di atas masih cukup baik untuk digunakan, namun sudut ikatan akan berbeda sedikit. Sebagai contohnya, ikatan ganda karbon pada alkena seperti etilena C2H4 adalah AX3E0, namun sudut ikatan tidaklah persis 120°. Hal yang sama juga dapat terlihat pada SOCl2 yang termasuk AX3E1, namun karena substituen X tidaklah sama, sudut XAX tidak akan sama.
Pengecualian[sunting | sunting sumber]
Terdapat berbagai kelompok senyawa yang geometrinya tidak dapat diprediksi secara tepat oleh teori VSEPR.
Senyawa logam transisi[sunting | sunting sumber]
Banyak senyawa logam transisi yang geometrinya tidak dapat dijelaskan menggunakan teori VSEPR.[6] Struktur beberapa senyawa ini, meliputi logam hidrida dan kompleks alkil seperti heksametiltungsten dapat diprediksi dengan tepat menggunakan teori VALBOND, yang didasarkan pada orbital hibrid sd dan model ikatan tiga-pusat empat-elektron.[7][8] Teori medan kristal merupakan teori sering dapat memprediksi geometri kompleks koordinasi.
Senyawa halida golongan 2[sunting | sunting sumber]
Struktur senyawa halida triatomik dengan logam golongan 2 tidaklah linear pada fase gas seperti yang diprediksi oleh teori VSEPR, melainkan berbentuk tekuk (sudut X-M-X:CaF2, 145°; SrF2, 120°; BaF2, 108°; SrCl2, 130°; BaCl2, 115°; BaBr2, 115°; BaI2, 105°).[9] Gillespie mengajukan bahwa ini disebabkan oleh interaksi ligan dengan elektron pada inti atom logam yang menyebabkan polarisasi atom, sehingga kelopak dalam atom tidaklah simetris berbentuk bola dan memengaruhi geometri molekul.[6][10]
Beberapa molekul AX2E2[sunting | sunting sumber]
Salah satu contohnya adalah molekul litium oksida Li2O yang berbentuk linear daripada berbentuk tekuk. Hal ini dikarenakan ikatan yang bersifat sangat ionik, menyebabkan gaya tolakan yang sangat kuat antara atom litium.[11]
Contoh lainnya adalah O(SiH3)2 dengan sudut Si-O-Si 144,1°. Hal ini berbeda dengan sudut pada Cl2O yang sebesar 110,9°, (CH3)2O 111.7°, dan N(CH3)3 110,9°. Gillespies mengajukan bahwa terdapat lokalisasi pasangan menyendiri, sehingga kemampuan pasangan menyendiri tersebut untuk menolak pasangan elektron lainnya akan menjadi sangat kuat ketika ligannya memiliki elektronegativitas yang sama ataupun lebih kuat daripada atom pusat.[6] Ketika atom pusat lebih elektronegatif, seperti pada O(SiH3)2, pasangan menyendirinya akan kurang terlokalisasi, sehingga memiliki gaya tolakan yang lebih lemah. Kombinasi efek ini dengan gaya tolak antar ligan akan menyebabkan sudut ikat Si-O-Si lebih besar daripada yang diprediksi.[6]
Beberapa molekul AX6E1[sunting | sunting sumber]
Beberapa molekul AX6E1, seperti anion Te(IV) dan Bi(III), TeCl62−, TeBr62−, BiCl63−, BiBr63− dan BiI63−, berbentuk oktahedron sempurna dan pasangan menyendirinya tidak memengaruhi geometri molekul.[12] Salah satu rasionalisasi pengamatan ini adalah bahwa sesakan sterik ligan tidak menyediakan ruang untuk pasangan menyendiri yang tidak berikatan,[6] rasionalisasi lainnya menjelaskannya menggunakan efek pasangan inert[13]
Lihat pula[sunting | sunting sumber]
Referensi[sunting | sunting sumber]
- ^ Modern Inorganic Chemistry W.L. Jolly ISBN 0-07-032760-2
- ^ http://www.jstor.org/pss/97507 N.V.Sidgwick and H.M.Powell, Proc.Roy.Soc.A 176, 153-180 (1940) Bakerian Lecture. Stereochemical Types and Valency Groups
- ^ R.J.Gillespie and R.S.Nyholm, Quart.Rev. 11, 339 (1957)
- ^ R.J.Gillespie, J.Chem.Educ. 47, 18(1970)
- ^ DOI:10.1016/S0022-1139(99)00194-3
- ^ a b c d e Models of molecular geometry, Gillespie R. J., Robinson E.A. Chem. Soc. Rev., 2005, 34, 396–407, DOI:10.1039/b405359c 10.1039/b405359c
- ^ Landis, C. K.; Cleveland, T.; Firman, T. K. Making sense of the shapes of simple metal hydrides. J. Am. Chem. Soc. 1995, 117, 1859-1860.
- ^ Landis, C. K.; Cleveland, T.; Firman, T. K. Structure of W(CH3)6. Science 1996, 272, 182-183.
- ^ Greenwood, Norman N.; Earnshaw, A. (1997), Chemistry of the Elements (edisi ke-2), Oxford: Butterworth-Heinemann, ISBN 0-7506-3365-4
- ^ Core Distortions and Geometries of the Difluorides and Dihydrides of Ca, Sr, and Ba Bytheway I, Gillespie R.J, Tang T.H., Bader R.F. Inorganic Chemistry, 34,9, 2407-2414, 1995 DOI:10.1021/ic00113a023
- ^ A spectroscopic determination of the bond length of the LiOLi molecule: Strong ionic bonding, D. Bellert, W. H. Breckenridge, J. Chem. Phys. 114, 2871 (2001); doi:10.1063/1.1349424
- ^ Wells A.F. (1984) Structural Inorganic Chemistry 5th edition Oxford Science Publications ISBN 0-19-855370-6
- ^ Catherine E. Housecroft, Alan G. Sharpe (2005), Inorganic Chemistry, Pearson Education, ISBN 0-13-039913-2