Resonansi stokastik

Resonansi stokastik adalah istilah yang pertama kali muncul 1[pranala nonaktif permanen] tahun 1981, di mana saat itu istilah tersebut diusulkan sebagai mekanisme yang dipercaya bagi terjadinya peristiwa-peristiwa hampir periodik (perioda mendekati 100.000 tahun) dari zaman es di Bumi selama 700.000 tahun belakangan ini. Sedangkan kelahiran resonansi stokastik dalam fenomena fisis terkendalikan secara eksperimen terjadi tahun 1983, setelah demonstrasi pertamanya dalam rangkaian elektronik Schmitt triggers.[1] Sejak saat itu resonansi stokastik tumbuh secara cepat dalam bidang-bidang pengembangan dan riset multi-disiplin, dengan berbagai manifestasi eksperimental dalam bidang-bidang biologi, laser, elektronik, kuantum dan sistem-sistem lain. Sampai saat ini masih banyak proposal-proposal teori yang menantikan verifikasinya secara eksperimen.[2]
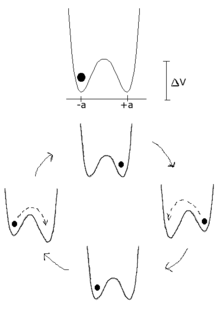
Resonansi stokastik adalah suatu fenomena di mana suatu sistem non-linier di bawah pengaruh suatu sinyal periodik termodulasi yang amat lemah sehingga secara normal tidak terdeteksi, akan tetapi dapat terdeteksi disebabkan terjadinya resonansi antara sinyal deterministik yang lemah tersebut dengan gangguan (noise) stokastik. Definisi paling awal dari resonansi stokastik adalah kekuatan sinyal keluaran maksimum sebagai fungsi dari gangguan (Bulsara dan Gammaitoni 1996).[3]
Sistem bistabil[sunting | sunting sumber]
Secara umum resonansi stokastik dibahas dalam kerangka sistem bistabil, yaitu di mana dalam sistem yang dimaksud terhadap hanya dua tingkat keadaan, di mana objek dari sistem, biasanya partikel, bisa berpindah dari dua keadaan stabil tersebut. Untuk mudahnya bayangkan suatu partikel berada dalam suatu lembah potensial yang di tengah-tengahnya terdapat bukit potensial sebagai pemisah. Bentuk potensial seperti ini dikenal dengan istilah sumur ganda (double well). Suatu bentuk sumur potensial ganda yang umum digunakan adalah
Tanpa adanya gangguan maka partikel akan berada hanya pada satu sumur, kiri atau kanan. Umumnya sinyal periodik yang digunakan dibuat sedemikian lemah sehingga partikel tidak dapat berpindah tempat atau 'hampir dapat berpindah'. Kemudian dengan mengenalkan gangguan, terjadilah resonansi pada sistem stokastik ini sehingga energi partikel menjadi tak terduga dalam domain temporal. Akibatnya pada saat yang tidak dapat diperkirakan sebelumnya, partikel dapat melompat ke ruang sebelahnya. Bentuk gangguan diilustrasikan seakan-akan meninggikan dasar sumur atau merendahkan bukit pemisah, sehingga partikel dapat melompat. Keadaan ini tidak dapat diperoleh bila gangguan dihilangkan.
Persamaan gerak partikel terkait dengan potensial dan sinyal masukannya, umumnya dituliskan sebagai
dengan , , dan berturut-turut adalah amplitudo, frekuensi dan fase dari signal masukan. Fungsi adalah gangguan yang bersifat stokastik sebagai fungsi waktu .
Struktur puncak-puncak[sunting | sunting sumber]
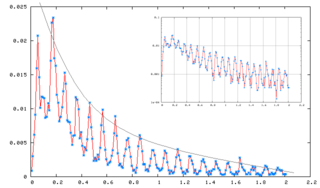
Terdapat suatu yang khas dalam sistem resonansi stokastik yaitu distribusi waktu yang dihabiskan partikel dalam satu ruang sumur memiliki puncak-puncak yang dikenal sebagai struktur puncak-puncak. Semakin lama partikel berada dalam suatu ruang sumur, semakin jarang hal itu terjadi. Sebaliknya semakin sebentar partikel berada dalam suatu ruang sumur, semakin sering peristiwa itu berulang. Di antara kedua kejadian tersebut terdapat pula rentang waktu yang tidak disukai, akibatnya terbentuklah struktur puncak-puncak ini.
Untuk mudahnya, bayangkan dua ruangan A dan B. Sebuah partikel dapat berada di ruang A maupun B selama waktu Δt. Bila dilakukan pengamatan dalam waktu yang amat lama maka akan diperoleh bahwa nilai-nilai Δt ini akan memenuhi suatu distribusi yang menunjukkan struktur puncak-puncak. Artinya terdapat suatu nilai Δt di mana memiliki kebolehjadian untuk terulang, akan tetapi terdapat pula Δt di mana kebolehjadian berulangnya amat kecil. Ini bisa disamakan seperti berapa lama seseorang dapat berada di suatu rumah makan. Ia bisa berada antara rentang Δt 10 menit (jika hanya memesan makanan untuk dibungkus) atau 2 jam (makan sambil mengobrol) akan tetapi kecil kemungkinan untuk berada hanya dalam waktu 2 detik atau 3 hari. Ilustrasi ini cocok untuk menerangkan puncak pertama dari struktur puncak-puncak.
Dalam sistem resonansi stokastik, bila telah terdapat suatu Δt yang disenangi, makan umumnya terdapat pula kelipatannya, akan tetapi dengan kebolehjadian yang lebih kecil. Tinggi dari Δt dan kelipatan-kelipatannya ini akan meluruh secara eksponensial sejalan dengan semakin besarnya Δt.
Contoh-contoh resonansi stokastik[sunting | sunting sumber]
Terdapat banyak contoh-contoh resonansi stokastik, beberapa di antaranya adalah rangkaian elektronik trigger Schmitt, diode tunnel, sistem biologi pada respon saraf penglihatan, kanal ionik, aplikasi medis, laser cincin bistabil dan devais interferensi kuantum super-menghantar.
Analisis[sunting | sunting sumber]
Resonansi stokastik dapat dianalisis dengan berbagai cara, salah satunya adalah dengan memperhatikan ciri khas spektrum-nya untuk kemudian dihitung rasio sinyal terhadap gangguan (signal to noise ratio atau SNR). Dengan cara ini, bentuk sinyal yang "mirip" dapat dibedakan lebih lanjut.
Rujukan[sunting | sunting sumber]
- ^ Fauve, S.; Heslot, F. (1983-08-08). "Stochastic resonance in a bistable system". Physics Letters A (dalam bahasa Inggris). 97 (1): 5–7. doi:10.1016/0375-9601(83)90086-5. ISSN 0375-9601.
- ^ Wellens, Thomas; Shatokhin, Vyacheslav; Buchleitner, Andreas (2004-01-01). "Stochastic resonance". Reports on Progress in Physics. 67 (1): 45–105. doi:10.1088/0034-4885/67/1/R02. ISSN 0034-4885.
- ^ Weisstein, Eric W. "Stochastic Resonance". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2023-05-16.
- (Inggris) Roberto Benzi, Alfonso Sutera and Angelo Vulpiani, The mechanism of stochastic resonance[pranala nonaktif permanen], J. Phys. A: Math. Gen. 14 (1981) L453-l457..
- (Inggris) Luca Gammaitoni, Peter Hänggi, Peter Jung and Fabio Marchesoni, Stochastic Resonance, Reviews of Modern Physics, Vol. 70, No. 1, January 1998.







