Medan listrik

| Artikel ini merupakan bagain dari seri |
| Listrik dan Magnet |
|---|
 |
Medan listrik adalah gaya listrik yang mempengaruhi ruang di sekeliling muatan listrik. Penyebab timbulnya medan listrik adalah keberadaan muatan listrik yang berjenis positif dan negatif. Medan listrik dapat digambarkan sebagai garis gaya atau garis medan.[1] Medan listrik memiliki satuan N/C atau dibaca Newton/coulomb. Medan listrik umumnya dipelajari dalam bidang fisika dan bidang-bidang terkait, dan secara tak langsung juga di bidang elektronika yang telah memanfaatkan medan listrik ini dalam kawat konduktor (kabel).
Asal medan listrik[sunting | sunting sumber]
Rumus matematika untuk medan listrik dapat diturunkan melalui Hukum Coulomb, yaitu gaya antara dua titik muatan:\
Menurut persamaan ini, gaya pada salah satu titik muatan berbanding lurus dengan besar muatannya. Medan listrik didefinisikan sebagai suatu konstan perbandingan antara muatan dan gaya:[2]
Maka, medan listrik bergantung pada posisi. Suatu medan, merupakan sebuah vektor yang bergantung pada vektor lainnya. Medan listrik dapat dianggap sebagai gradien dari potensial listrik. Jika beberapa muatan yang disebarkan menghasilkan potensial listrik, gradien potensial listrik dapat ditentukan.
Konstanta k[sunting | sunting sumber]
Dalam rumus listrik sering ditemui konstanta k sebagai ganti dari (dalam tulisan ini tetap digunakan yang terakhir), di mana konstanta tersebut bernilai:[3]
yang kerap disebut konstanta kesetaraan gaya listrik.[4]
Menghitung medan listrik[sunting | sunting sumber]

Untuk menghitung medan listrik di suatu titik akibat adanya sebuah titik muatan yang terletak di digunakan rumus [5]
Penyederhanaan yang kurang tepat[sunting | sunting sumber]
Umumnya untuk melakukan penyederhanaan dipilih pusat koordinat berhimpit dengan titik muatan yang terletak di sehingga diperoleh rumus seperti telah dituliskan pada permulaan artikel ini, atau bila dituliskan kembali dalam notasi vektornya:
dengan vektor satuan
Disarankan untuk menggunakan rumusan yang melibatkan dan karena lebih umum, dan dapat diterapkan untuk kasus lebih dari satu muatan dan juga pada distribusi muatan, baik distribusi diskrit maupun kontinu. Penyederhanaan ini juga kadang membuat pemahaman dalam menghitung medan listrik menjadi agak sedikit kabur. Selain itu pula karena penyederhanaan ini hanya merupakan salah satu kasus khusus dalam perhitungan medan listrik (kasus oleh satu titik muatan di mana titik muatan diletakkan di pusat koordinat).
Tanda muatan listrik[sunting | sunting sumber]

Muatan listrik dapat bernilai positif, nol (tidak terdapat muatan atau jumlah satuan muatan positif dan negatif sama) dan negatif. Nilai muatan ini akan memengaruhi perhitungan medan listrik dalam hal tandanya, yaitu positif atau negatif (atau nol). Apabila pada setiap titik di sekitar sebuah (atau beberapa) muatan dihitung medan listriknya dan digambarkan vektor-vektornya, akan terlihat garis-garis yang saling berhubungan, yang disebut sebagai garis-garis medan listrik. Tanda muatan menentukan apakah garis-garis medan listrik yang disebabkannya berasal darinya atau menuju darinya. Telah ditentukan (berdasarkan gaya yang dialami oleh muatan uji positif), bahwa
- muatan positif
(+)akan menyebabkan garis-garis medan listrik berarah dari padanya menuju keluar, - muatan negatif
(-)akan menyebabkan garis-garis medan listrik berarah menuju masuk padanya. - muatan nol
( )tidak menyebabkan adanya garis-garis medan listrik.
Gradien potensial listrik[sunting | sunting sumber]
Medan listrik dapat pula dihitung apabila suatu potensial listrik diketahui, melalui perhitungan gradiennya:[6]
dengan
untuk sistem koordinat Kartesius.
Energi medan listrik[sunting | sunting sumber]
Medan listrik menyimpan energi. Rapat energi suatu medan listrik diberikan oleh [7]
dengan
- adalah permittivitas medium di mana medan listrik terdapat, dalam vakum .
- adalah vektor medan listrik.
Total energi yang tersimpan pada medan listrik dalam suatu volum adalah
dengan
- adalah elemen diferensial volum.
Distribusi muatan listrik[sunting | sunting sumber]
Medan listrik tidak perlu hanya ditimbulkan oleh satu muatan listrik, melainkan dapat pula ditimbulkan oleh lebih dari satu muatan listrik, bahkan oleh distribusi muatan listrik baik yang diskrit maupun kontinu. Contoh-contoh distribusi muatan listrik misalnya:
- kumpulan titik-titik muatan
- kawat panjang lurus berhingga dan tak-berhingga
- lingkaran kawat
- pelat lebar berhingga atau tak-berhingga
- cakram tipis dan cincin
- bentuk-bentuk lain
Kumpulan titik-titik muatan[sunting | sunting sumber]
Untuk titik-titik muatan yang tersebar dan berjumlah tidak terlalu banyak, medan listrik pada suatu titik (dan bukan pada salah satu titik muatan) dapat dihitung dengan menjumlahkan vektor medan listrik di titik tersebut akibat oleh masing-masing muatan. Dalam kasus ini lebih baik dituliskan
yang dibaca, medan listrik di titik akibat adanya muatan yang terletak di . Dengan demikian medan listrik di titik akibat seluruh muatan yang tersebar dituliskan sebagai
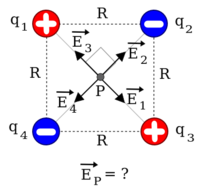
di mana adalah jumlah titik muatan. Sebagai ilustrasi, misalnya ingin ditentukan besarnya medan listrik pada titik yang merupakan perpotongan kedua diagonal suatu bujursangkar bersisi , di mana terdapat oleh empat buat muatan titik yang terletak pada titik sudut-titik sudut bujursangkar tersebut. Untuk kasus ini misalkan bahwa dan dan ambil pusat koordinat di titik untuk memudahkan. Untuk kasus dua dimensi seperti ini, bisa dituliskan pula
yang akan memberikan
sehingga
yang menghasilkan bahwa medan listrik pada titik tersebut adalah nol.
Kawat panjang lurus[sunting | sunting sumber]
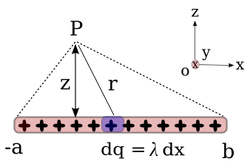
Kawat panjang lurus merupakan salah satu bentuk distribusi muatan yang menarik karena bila panjangnya diambil tak-hingga, perhitungan muatan di suatu jarak dari kawat dan terletak di tengah-tengah panjangnya, menjadi amat mudah.
Untuk suatu kawat yang merentang lurus pada sumbu , pada jarak di atasnya, dengan kawat merentang dari sampai dari titik proyeksi pada kawat, medan listrik di titik tersebut dapat dihitung besarnya, yaitu:
Seperti telah disebutkan di atas, apabila dan maka dengan menggunakan dalil L'Hospital diperoleh
Atau bila kawat diletakkan sejajar dengan sumbu-z dan bidang x-y ditembus kawat secara tegak lurus, maka medan listrik di suatu titik berjarak dari kawat, dapat dituliskan medan listriknya adalah
dengan adalah vektor satuan radial dalam koordinat silinder:
di mana adalah sudut yang dibentuk dengan sumbu-x positif.
Pranala luar[sunting | sunting sumber]
- Electric field in "Electricity and Magnetism", R Nave – Hyperphysics, Georgia State University
- 'Gauss's Law' – Chapter 24 of Frank Wolfs's lectures at University of Rochester
- 'The Electric Field' – Chapter 23 of Frank Wolfs's lectures at University of Rochester
- [1] – An applet that shows the electric field of a moving point charge.
- Fields Diarsipkan 2010-05-27 di Wayback Machine. – a chapter from an online textbook
- Learning by Simulations Interactive simulation of an electric field of up to four point charges
- Java simulations of electrostatics in 2-D and 3-D
- Interactive Flash simulation picturing the electric field of user-defined or preselected sets of point charges by field vectors, field lines, or equipotential lines. Author: David Chappell
Referensi[sunting | sunting sumber]
- ^ Soebyakto (2017). Fisika Terapan 2 (PDF). Tegal: Badan Penerbit Universitas Pancasakti Tegal. hlm. 2. ISBN 978-602-73169-4-2.
- ^ Andrew Duffy, Electric field, PY106/Electricfield.html, 7-7-99.
- ^ Reference Tables for Physical setting/Physics, 2002 Edition, The University of The State of New York, 2002.
- ^ J.S. Covacs, Coulomb's Law, PhysNet, MISN-0-114, hal 3 Diarsipkan 2006-11-10 di Wayback Machine.
- ^ Tulisan ini menggunakan dua jenis notasi vektor yang berbeda untuk merujuk hal yang sama:
- vektor (dengan panah di atasnya), dan
- vektor (dicetak tebal).
- ^ Carl R. Nave, Electric Field as Gradient, HyperPhysics, electric/efromv.html#c2, 2006.
- ^ David Land, Electrostatic field energy, ELMAG305/em8a/sld006.htm Diarsipkan 2006-08-21 di Wayback Machine., 18.10.1999 17:05:51.


















































![{\displaystyle E_{z}={\frac {1}{4\pi \epsilon _{0}}}\ {\frac {\lambda }{z}}\ \left[{\frac {b}{\sqrt {z^{2}+b^{2}}}}+{\frac {a}{\sqrt {z^{2}+a^{2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ceee72cecfd32cf200b0cf40ad232e285c583d74)








