Gelanggang Borromean

Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Gelanggang Borromean
L6a4
Panjang kepangan6[[Kategori:Buhul dan jalinan panjang kepangan {{{panjang kepangan}}}]]
Bil. kepangan3[[Kategori:Buhul dan jalinan bilangan kepangan {{{bilangan kepangan}}}]]
Bil. penyilangan6[[Kategori: Buhul dan jalinan bilangan penyilangan {{{bilangan penyilangan}}}]]
Volume hiperbolik7.327724753
Bil. lekat9[[Kategori:buhul dan jalinan bilangan lekat {{{bilangan lekat}}}]]
Bil. takbuhulan2
Notasi Conway[.1]
Notasi A–B632
ThistlethwaiteL6a4
Last /NextL6a3 / L6a5
Other
saling bergantian, hiperbolis


Dalam matematika, gelanggang Borromean[a] terdiri dari tiga lingkaran topologi yang terhubung dan membentuk tautan Brunnian (di mana apabila satu cincin keluar, maka akan menghasilkan dua cincin yang tidak terhubung). Dengan kata lain, tidak ada dua dari tiga cincin yang saling berkait satu sama lain sebagai jalinan Hopf, tetapi ketiga cincin tersebut tetap saja saling terkait.

Cincin-cincin Borromean

Sifat matematika[sunting | sunting sumber]

Ketidakmungkinan cincin melingkar sempurna[sunting | sunting sumber]

Meskipun gambar khas cincin-cincin Borromean (pada gambar sebelah kanan di atas) menyebabkan seseorang berpikir bahwa tautan tersebut dapat terbentuk dari cincin lingkaran geometris yang ideal, tetapi hal ini sebenenarnya merupakan suatu hal yang tidak mungkin tejadi. Freedman dan Skora (1987) membuktikan bahwa suatu kelas tautan tertentu, seperti pada tautan Borromean, persisnya tidak dapat saling melingkar. Sebagai alternatif, hal ini dapat dilihat dengan adanya asumsi diagram tautan: jika seseorang mengasumsikan bahwa lingkaran 1 dan 2 menyentuh kedua titik persimpangan masing-masing, maka keduanya akan membentang pada suatu bidang datar atau bola. Dalam kedua kasus tersebut, lingkaran ketiga harus melewati bidang datar atau bola selama empat kali, tanpa membentang ke dalamnya, di mana hal ini tidak memungkinkan, lihat (Lindström & Zetterström 1991).

Realisasi dari cincin Borromean sebagai elips
Gambar Cincin Borromean 3D

Namun, bagaimanapun, hal ini dapat menjadi mungkin, apabila seseorang menggunakan elips (lihat gambar kanan). Hal ini dianggap sebagai eksentrisitas arbitrer kecil; tidak peduli seberapa presisi bentuk lingkarannya, selama tidak berbentuk lingkaran sempurna, maka lingkaran-lingkaran ini dapat membentuk tautan Borromean jika sesuai; contohnya, lingkaran tipis dari kawat elastis yang dapat ditekuk dapat digunakan sebagai cincin Borromean.

Hubungan dengan graf oktahedral[sunting | sunting sumber]

Selain menunjukkan untai mana yang menyilang di atas satu sama lain, diagram tautan menggunakan notasi yang sama dalam menunjukkan dua alur persimpangan, seperti graf yang digunakan dalam menunjukkan empat sisi yang saling bertemu pada simpul biasa. Dengan demikian, graf oktahedron reguler dapat diubah menjadi diagram tautan yang dikonversi menjadi untaian yang mengikuti tepi berturutan, yang dengannya melewati simpul dan melewati bagian bawah berikutnya secara bergantian. Hasilnya terdiri dari tiga putaran (loop) terpisah, yang dihubungkan bersamaan menjadi cincin Borromean.[1]

Pertautan[sunting | sunting sumber]

Informasi lebih lanjut: Grup tautan

Dalam teori simpul, cincin Borromean merupakan contoh sederhana dari tautan Brunnian, di mana masing-masing cincin tidak terhubung, serta tautan tersebut tidak dapat dilepaskan tautannya secara keseluruhan. Terdapat pula beberapa cara untuk melihat hal ini.

Tautan yang paling sederhana memiliki grup fundamental dari dua lingkaran komplementer, yang tak terkait, yang merupakan grup bebas yang dibangun dua unsur, a dan b, pada teorema Seifert-van Kampen, kemudian loop ketiga memiliki kelas komutator, [a, b] = aba−1b−1, seperti yang dapat dilihat pada diagram tautan: melampaui yang satu, melampaui yang berikutnya, kembali lagi ke bagian bawah yang pertama, lalu kembali lagi pada yang kedua. Didapat loop yang non-trivial dalam grup fundamentalnya sehingga cincin Borromean saling bertautan.

Cara lain adalah bahwa kohomologi dari komplementasi yang mendukung konsep Massey product yang non-trivia, yang bukan penyebab penghilangan tautan. Hal ini merupakan contoh sederhana dari konsep Massey product, di mana aljabar sesuai dengan geometri: Massey product 3-manifold merupakan hasil kali 3-manifold yang hanya ditentukan jika semua product 2-manifold tidak bertaut, di mana cincin Borromean yang dipasangkan secara berpasangan (hasil kali 2-manifold hilang), tetapi terkait secara keseluruhan (di mana hasil kali 3-manifold tidak hilang).

Dalam topologi aritmatika, terdapat analogi antara simpul dan bilangan prima, yaitu adanya hubungan-hubungan antara bilangan prima. Tiga bilangan prima (13, 61, 937) dihubungkan modulo 2 (simbol Rédei adalah -1), tetapi dipasangkan dengan pasangan modulo 2 (simbol Legendre yang semuanya 1). Oleh karena itu, bilangan prima ini disebut "triple Borromean modulo 2"[2] atau "bilangan prima mod 2 Borromean".[3]

Geometri hiperbolik[sunting | sunting sumber]

Cincin Borromean merupakan tautan hiperbolik: komplementasi cincin Borromean dalam bola-3 yang memuat metrik hiperbolik lengkap dengan volume terbatas. Dekomposisi polihedral kanonikal (Epstein-Penner) dari komplementasi yang terdiri dari dua oktahedra ideal biasa. Volumenya adalah 16Л (π / 4) = 7.32772 ... di mana Л adalah fungsi Lobachevsky.[4]

Hubungan dengan kepang[sunting | sunting sumber]

Tiga tali ikat standar yang menyerupai cincin Borromean.

Jika seseorang memotong cincin Borromean, maka dapat diperoleh satu iterasi jalinan standar; sebaliknya, jika menghubungkan ujung-ujung (dari satu iterasi) kepang standar, maka dapat diperoleh cincin Borromean. Sama halnya seperti menghilangkan satu cincin Borromean yang dapat memutuskan dua untaian lainnya, dengan mengeluarkan satu untaian kepang standar yang tidak bertaut dengan dua kepang lainnya, di mana keduanya merupakan tautan Brunnian dasar dan kepang Brunnian.

Dalam diagram tautan standar, cincin Borromean disusun secara non-transit, dalam urutan siklis. Dengan menggunakan warna di atas, warna merah di atas biru muda, biru muda di atas biru, biru di atas merah; oleh karenanya setelah mengeluarkan satu cincin, maka dua cincin yang tersisa, di mana yang satu berada di atas yang lainnya, yang keduanya dapat dipisahkan. Demikian pula, dalam kepang standar, masing-masing untai berada di atas yang lainnya dan pada waktu yang sama berada di bawah yang lainnya.

Sejarah[sunting | sunting sumber]

Cincin Borromean sebagai simbol Tritunggal Kristen, dari manuskrip abad ke-13.
Valknut di batu Stora Hammars I

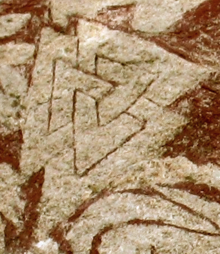
Nama "cincin Borromean" berasal dari penggunaannya sebagai lambang keluarga aristokrat Borromeo di Italia Utara. Tautan itu sendiri sudah jauh lebih tua dan telah muncul dalam bentuk valknut pada gambar batu Suku Norse di abad ke-7. Cincin Borromean telah digunakan dalam konteks berbeda dalam menjelaskan kekuatan dalam kesatuan, misalnya, dalam agama atau seni. Secara khusus, beberapa diantaranya menggunakan desain ini untuk melambangkan Tritunggal. Psikoanalis terkenal, Jacques Lacan menemukan inspirasi dalam cincin Borromean sebagai model topologi subjektivitas manusia, di mana masing-masing cincin mewakili komponen realitas mendasar Lacanian (yaitu tatanan "riil", "imajiner", dan "simbolik").

Cincin ini juga digunakan sebagai logo bir Ballantine, dan masih digunakan sebagai merek bir Ballantine, yang kini didistribusikan oleh pemilik merek saat ini, yaitu Pabst Brewing Company.

Sebuah simpul tinju monyet

Cincin Borromean, karena sifat matematisnya, ditampilkan oleh Martin Gardner pada kolom "Permainan Matematika" dalam Scientific American pada September 1961.

Pada tahun 2006, Serikat Matematika Internasional memutuskan pada Kongres Internasional Matematikawan ke-25 di Madrid, Spanyol supaya menggunakan logo baru yang berdasarkan cincin Borromean.[5]

Sebuah pilar batu di Kuil Marundeeswarar di Thiruvanmiyur, Chennai, Tamil Nadu, India, memiliki sosok seperti ini sebelum abad ke-6.[6][7]

"Mandala" diskordian, yang berisi lima konfigurasi cincin Borromean

Cincin parsial[sunting | sunting sumber]

Di Eropa abad pertengahan dan renaisans, sejumlah tanda visual ditemukan yang terdiri dari tiga elemen yang saling terkait sedemikian rupa sehingga cincin Borromean ditunjukkan saling terkait (dalam penggambaran dua dimensi konvensional mereka), tetapi elemen-elemen individualnya tidak tertutup. Contoh simbol semacam itu adalah tanduk batu Snoldelev dan bulan sabit Diana dari Poitiers. Contoh tiga elemen berbeda misalnya logo Sport Club Internacional. Tanda visual yang kurang terkait mencakup diagram Gankyil dan Venn pada tiga pasangan.

Demikian pula, simpul tinju monyet pada dasarnya adalah representasi cincin Borromean tiga dimensi, meskipun memiliki tiga lapisan, dalam banyak kasus.

Dengan menggunakan pola cincin Borromean yang tidak lengkap, seseorang dapat menyeimbangkan tiga pisau pada tiga penopang, seperti tiga botol atau gelas, yang dapat menopang pada bagian tengah pada botol atau gelas keempat.[8]

Cincin dengan kelipatan[sunting | sunting sumber]

Beberapa simpul-teoretis memiliki kelipatan konfigurasi pada cincin Borromean; di mana satu tautan memiliki lima lingkaran (loop) seperti simbol Diskordianisme, yang didasarkan pada sebuah penggambaran dalam Principia Discordia.

Realisasi[sunting | sunting sumber]

Struktur kristal dari cincin Borromean molekuler yang dilaporkan oleh Stoddart dkk. (Science 2004)[9]

Cincin Borromean Molekuler merupakan lingkaran molekul cincin Borromean, yang memiliki struktur molekul mekanis yang saling terkait. Pada tahun 1997, ahli biologi Chengde Mao dan rekan kerjanya dari Universitas New York berhasil membangun seperangkat cincin dari DNA.[10] Pada tahun 2003, ahli kimia Fraser Stoddart dan rekan kerjanya di UCLA menggunakan koordinasi kimia dalam membangun satu set cincin dalam satu langkah dari 18 komponen. Sebuah perpustakaan jaringan Borromean telah disintesis dengan sengaja oleh Giuseppe Resnati dan rekan kerjanya melalui ikatan halogen mandiri.[11]

Sebuah analog kuantum mekanis dari cincin Borromean disebut dengan keadaan halo atau keadaan Efimov (di mana keberadaan suatu keadaan seperti itu telah diprediksi oleh ahli fisika Vitaly Efimov, pada tahun 1970). Untuk pertama kalinya kelompok riset Rudolf Grimm dan Hanns-Christoph Nägerl dari Institut Fisika Eksperimental (Universitas Innsbruck, Austria) mengkonfirmasi melalui sebuah percobaan dengan keadaan semacam itu dalam gas ultracold dari atom sesium pada tahun 2006, serta menerbitkan temuan mereka dalam jurnal ilmiah Nature.[12] Sebuah tim fisikawan yang dipimpin oleh Randall Hulet dari Universitas Rice di Houston, mencapai hal ini dengan satu set dari tiga atom litium terikat dan menerbitkan temuan mereka pada jurnal daring Science Express.[13] Pada tahun 2010, sebuah tim yang dipimpin oleh K. Tanaka menciptakan sebuah keadaan Efimov di dalam sebuah sel inti.[14]

Lihat pula[sunting | sunting sumber]

Catatan[sunting | sunting sumber]

  1. ^ Dinamai setelah digunakan sebagai lambang keluarga Borromeo di abad ke-15 di Lombardy.

Referensi[sunting | sunting sumber]

  1. ^ N. L. Biggs (1 March 1981). "T. P. Kirkman Mathematician". Bull. London Math. Soc. 13 (2): 116. doi:10.1112/blms/13.2.97. Diarsipkan dari versi asli tanggal 2020-03-12. Diakses tanggal 24 January 2017. 
  2. ^ Denis Vogel (13 February 2004), Massey products in the Galois cohomology of number fields, urn:nbn:de:bsz:16-opus-44188, diarsipkan dari versi asli tanggal 2023-07-29, diakses tanggal 2018-02-05 
  3. ^ Masanori Morishita (22 April 2009), Analogies between Knots and Primes, 3-Manifolds and Number Rings, arXiv:0904.3399 alt=Dapat diakses gratis 
  4. ^ William Thurston (March 2002), "7. Computation of volume" (PDF), The Geometry and Topology of Three-Manifolds, hlm. 165, diarsipkan dari versi asli tanggal 2020-07-27, diakses tanggal 2018-02-05 
  5. ^ "ICM 2006" (PDF). Diarsipkan dari versi asli (PDF) tanggal 2016-03-03. Diakses tanggal 2018-02-05. 
  6. ^ Arul Lakshminarayan (May 2007). "Borromean Triangles and Prime Knots in an Ancient Temple" (PDF). Indian Academy of Sciences. Diarsipkan (PDF) dari versi asli tanggal 2021-09-27. Diakses tanggal 18 September 2014. 
  7. ^ Blog entry by Arul Lakshminarayan
  8. ^ "Comments on Knives And Beer Bar Trick: Amazing Balance". Diarsipkan dari versi asli tanggal 2018-02-06. Diakses tanggal 2018-02-05. 
  9. ^ Kelly S. Chichak; Stuart J. Cantrill; Anthony R. Pease; Sheng-Hsien Chiu; Gareth W. V. Cave; Jerry L. Atwood; J. Fraser Stoddart (28 May 2004). "Molecular Borromean Rings". Science. 304 (5675): 1308–1312. 
  10. ^ C. Mao; W. Sun; N. C. Seeman (1997). "Assembly of Borromean rings from DNA". Nature. 386 (6621): 137–138. doi:10.1038/386137b0. PMID 9062186. 
  11. ^ Giuseppe Resnati; et al. (2017). "Halogen bonded Borromean networks by design: topology invariance and metric tuning in a library of multi-component systems". Chemical Science. doi:10.1039/C6SC04478F. CS1 maint: Explicit use of et al. (link)
  12. ^ T. Kraemer; M. Mark; P. Waldburger; J. G. Danzl; C. Chin; B. Engeser; A. D. Lange; K. Pilch; A. Jaakkola; H.-C. Nägerl; R. Grimm (2006). "Evidence for Efimov quantum states in an ultracold gas of caesium atoms". Nature. 440 (7082): 315–318. arXiv:cond-mat/0512394 alt=Dapat diakses gratis. Bibcode:2006Natur.440..315K. doi:10.1038/nature04626. PMID 16541068. 
  13. ^ Clara Moskowitz (December 16, 2009), Strange Physical Theory Proved After Nearly 40 Years, Live Science, diarsipkan dari versi asli tanggal 2023-07-29, diakses tanggal 2018-02-05 
  14. ^ K. Tanaka (2010), "Observation of a Large Reaction Cross Section in the Drip-Line Nucleus 22C", Physical Review Letters, 104 (6): 062701, doi:10.1103/PhysRevLett.104.062701 

Bacaan lanjut[sunting | sunting sumber]

  • P. R. Cromwell, E. Beltrami and M. Rampichini, "The Borromean Rings", Mathematical Intelligencer Vol. 20 no. 1 (1998) 53–62.
  • Freedman, Michael H.; Skora, Richard (1987), "Actions of Groups", Journal of Differential Geometry, 25: 75–98 
  • Lindström, Bernt; Zetterström, Hans-Olov (1991), "Borromean Circles are Impossible", American Mathematical Monthly, 98 (4): 340–341, doi:10.2307/2323803, JSTOR 2323803 (perlu berlangganan). Artikel ini menjelaskan mengapa tautan Borromean tidak persis berbentuk lingkaran. 
  • Brown, R. and Robinson, J., "Borromean circles", Letter, American Math. Monthly, April, (1992) 376–377. Artikel ini menunjukkan bagaimana persegi Borromean ada, dan telah berhasil dibuat oleh John Robinson (pematung), yang telah memberikan bentuk-bentuk lainnya Diarsipkan 2008-04-04 di Wayback Machine. pada struktur ini.
  • Chernoff, W. W., "Interwoven polygonal frames". (English summary) 15th British Combinatorial Conference (Stirling, 1995). Discrete Math. 167/168 (1997), 197–204. Artikel ini memberikan jalinan poligonal yang lebih umum.

Pranala luar[sunting | sunting sumber]

Wikimedia Commons memiliki media mengenai Borromean rings.
Diperoleh dari "https://id.wikipedia.org/w/index.php?title=Gelanggang_Borromean&oldid=23925014"