Proses adiabatik
| Termodinamika |
|---|
 |
Proses adiabatik (/ˌædiəˈbætɪk/; dari bahasa Yunani "a" + "diavaton") adalah proses yang muncul tanpa perpindahan panas dan massa antara sistem dan lingkungannya.[1][2] Proses ini merupakan salah satu konsep penting dalam termodinamika dalam pengembangan hukum pertama termodinamika.
Proses adiabatik berlangsung dalam dinding yang disolasi termal sepenuhnya dan tak dapat ditembus benda.
Gas Ideal (proses reversibel)[sunting | sunting sumber]
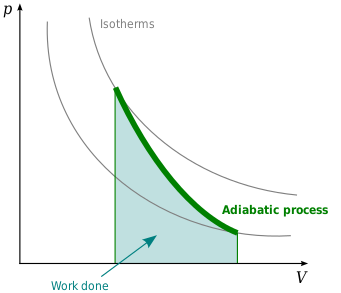
Persamaan matematika untuk gas ideal yang mengalami proses adiabatik reversibel adalah
dengan P adalah tekanan, V adalah volume, dan
adalah panas spesifik pada tekanan konstan, adalah panas spesifik pada volume konstan, adalah indeks adiabatik, dan adalah derajat kebebasan (3 untuk gas monoatomik, 5 untuk gas diatomik dan senyawa sederhana, seperti karbon dioksida).
Untuk gas ideal monoatomik, , dan untuk gas diatomik (seperti nitrogen dan oksigen) .[3] Perhatikan bahwa rumus diatas hanya berlaku untuk gas ideal klasik dan bukan Bose–Einstein atau gas Fermi.
Untuk proses adiabatik reversibel, juga berlaku hubungan
dengan T adalah temperatur absolut.
Dapat juga dituliskan
Ekspansi adiabatik bebas dari suatu gas[sunting | sunting sumber]
Untuk ekspansi adiabatik bebas dari suatu gas ideal, gas diletakkan dalam suatu kontainer terisolasi dan mengembang dalam vakum. Karena tidak ada tekanan luar untuk gas, maka kerja yang dilakukan oleh atau ke sistem adalah nol. Karena tidak ada perubahan panas atau kerja, maka menurut hukum pertama termodinamika, perubahan energi dalam adalah nol. Untuk gas ideal, temperatur tetap konstan karena energi dalam hanya bergantung pada temperatur untuk kasus ini. Pada temperatur konstan, entropi berbanding lurus dengan volume, sehingga entropi juga naik, maka proses ini tergolong ireversibel
Penurunan rumus pemanasan dan pendinginan adiabatik[sunting | sunting sumber]
Definisi dari proses adiabatik adalah tidak ada perpindahan panas ke dalam sistem, . Maka, menurut hukum pertama termodinamika,
dengan dU adalah perubahan energi dalam sistem dan δW adalah kerja yang dilakukan oleh sistem. Semua kerja (δW) yang dilakukan besarnya sala dengan perubahan energi dalam U karena tidak ada panas δQ yang masuk dari lingkungan. Kerja tekanan-volume δW yang dilakukan oleh sistem didefinisikan
Meski begitu, P tidak konstan pada proses adiabatik tapi turut berubah seiring dengan perubahan V.
Maka perlu diketahui berapa nilai dP dan dV berhubungan satu sama lain. Untuk gas ideal, energi dalamor an ideal gas the internal energy is given by
dengan adalah angka derajat kebebasan dibagi 2, R adalah konstanta gas universal, dan n adalah jumlah mol pada sistem.
Turunkan persamaan (3) dan menggunakan hukum gas ideal, , menghasilkan
Persamaan (4) sering dituliskan sebagai karena .
Substitusi persamaan (2) dan (4) ke persamaan (1) sehingga
gabungkan::
bagi kedua sisi dengan PV:
Setelah mengintegralkan sisi kiri dan kanan dari sampai V dan dari sampai P maka menjadi,
Eksponenkan kedua sisi, kemudian substitusi dengan , rasio kapasitas panas
Hilangkan tanda negatif dan didapatkan
Maka:
dan
Penurunan rumus diskrit[sunting | sunting sumber]
Perubahan energi dalam sistem, diukur dari keadaan 1 ke keadaan 2, sama dengan
Di waktu yang sama, kerja yang dilakukan oleh perubahan tekanan-volume sebagai hasil proses ini, sama dengan
Karena prosesnya adiabatik, maka persamaan hukum pertama termodinamika menjadi
Dengan persamaan sebelumnya,
Susun ulang persamaan (4) menjadi
Substitusi ke (2)
Diintegralkan
Substitusi ,
Disusun ulang,
Menggunakan persamaan gas ideal dan mengasumsikan kuantitas molar konstan,
Dengan rumus,
atau
Substitusi ke persamaan sebelumnya untuk ,
Substitusi persamaan ini dan (1) ke (3) menghasilkan
Sederhanakan,
Sederhanakan,
Sederhanakan,
Referensi[sunting | sunting sumber]
- ^ Carathéodory, C. (1909). Untersuchungen über die Grundlagen der Thermodynamik, Mathematische Annalen, 67: 355–386, DOI:10.1007/BF01450409. A translation may be found here. Also a mostly reliable translation is to be found at Kestin, J. (1976). The Second Law of Thermodynamics, Dowden, Hutchinson & Ross, Stroudsburg PA.
- ^ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 21.
- ^ Adiabatic Processes
- Silbey, Robert J.; et al. (2004). Physical chemistry. Hoboken: Wiley. hlm. 55. ISBN 978-0-471-21504-2.
- Broholm, Collin. "Adiabatic free expansion." Physics & Astronomy @ Johns Hopkins University. N.p., 26 Nov. 1997. Web. 14 Apr. *Nave, Carl Rod. "Adiabatic Processes." HyperPhysics. N.p., n.d. Web. 14 Apr. 2011. [1].
- Thorngren, Dr. Jane R.. "Adiabatic Processes." Daphne – A Palomar College Web Server. N.p., 21 July 1995. Web. 14 Apr. 2011. [2] Diarsipkan 2011-05-09 di Wayback Machine..























































